首先考虑归并排序:
归并排序为什么能相比普通的排序方法,将时间复杂度从O(n^2)提升至O(nlogn)?
最主要的一点是引入了两个有序数组合并的思想,真正提升效率就是在这个地方。
首先我们考虑,如果两个数组无序的话,比如:

如果使用O(n^2)的方法,在这样一个数组中,每一个数都要跟其他的数比较一下,这样复杂度就为n*n=n^2
而如果这两个数组是有序的呢?
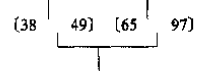
我们用两个指针p1和p2分别指向两个数组的尾部:
首先49比97小,97放入排序数组的尾部,因为它是最大的;
然后移动p2至65,再次与49做对比,将65放入倒数第二个位置,因为这是次大的。
然后我们就不需要比较了,因为38比49一定小,因此对38来说他不用比较一次。
这样我们看两个有序数组的排序实际上复杂度只需要O(m+n)
对于同样一个数38,我们在O(n^2)的方法中仍然要与49比,与65比,与97比,比完了之后才发现,哦原来我是最小的。
但是在两个有序数组的排序中,38是完全不用比较一次的。
因为数组的有序提供了额外信息,比如49比65和97都小,连比38大的数都比65和97小,那38我们还用比较吗?
这就是有序数组提供额外信息对我们排序效率提升的地方。
而这种额外信息是有代价的,这个代价就是logn的代价,也就是说将整个数组不断分治,分为logn层,每一层利用上一层的额外信息进行排序,排序后作为下一层的额外信息。
因此实际上归并排序nlogn的复杂度的来源就是:将无序数组排序问题转变成两个有序数组的排序问题,这样使复杂度从n^2提升至n,但有序又需要付出logn的代价,因此实际上对某一层来说,复杂度为O(n),共有logn层,来时间复杂度为O(nlogn).
有一点值得注意的是,如果在两个有序数组的合并过程中,不采用这种双指针的排序方式,还采取普通的O(n^2)的排序方式,复杂度不会有任何改善。
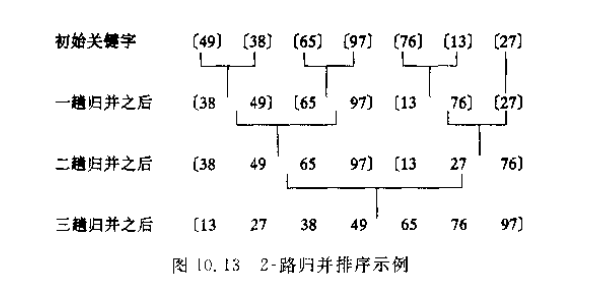
以下图中38为例:
38在第一次排序中跟49比,在第二次排序中跟65和97所在的数组比,在第三次跟76,13,27所在的数组比,实际上对某个数来说,在归并排序的过程中他还是在跟数组中所有的数在比较,只是在某些过程中的某些比较被避免了,从而提升了效率,比如在49和65与97比完后,38本来是要跟65和97比的,但由于38和49是有序的,我们知道了这种比较是没必要的,因此将这种比较省略了。
本质上,归并还是相当于某个数跟数组中所有的数都比较后找到自己应该属于的位置,但由于分治归并的思想,规避了这些比较中没必要的比较,从而提升了效率。
就像普通排序中38要跟所有的数比,而归并中,它的某些比较被省去了而已,但从流程上来说,每次数组合并,像[38 49]与[65 97]合并,[38 49 65 97]与[13 27 76]合并,38都还是要与另一个数组中的数做比较的,只是因为有序数组合并的算法,规避了某些没必要进行的排序。
下面进入正题,对数组中的逆序这道题的分析:
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。
输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
首先我们最容易想到的思路就是暴力搜索,对某个位置i的元素,将i+1~end的所有元素斗鱼i位置的元素相比。
但这种方式的复杂度太高了,O(n^2)的复杂度,在这个题里面一定是会超时的。
然后我们在仔细思考这个题:
以 5 6 2 1这个序列来说:
我们对5使用这个搜索过程,得到对于5,它的逆序对个数是2。
但如果[5 6]和[2 1]都是有序的,也就是[5 6] [1 2]时,5与[1]的对比是没有必要的,因为5已经比这个数组中最大的2都要大了,那肯定能和2以前的所有元素组成逆序对。
这个思路是不是很熟悉?
在上面进行归并排序时,我们对49 38 65 97排序时就是如此,对于有序的[38 49]和[65 97],我们不用对38在做比较了。
因此我们可以利用这个思路:
对[5 6] [2 1]先转变为有序,在进行逆序对计算。
前面提过:
本质上,归并还是相当于某个数跟数组中所有的数都比较后找到自己应该属于的位置,但由于分治归并的思想,规避了这些比较中没必要的比较,从而提升了效率。
在合并的过程中,某个数起始本质上还是在不断的在与在它后面位置的元素作比较,只是因为有序的存在,从而导致规避了没有必要的比较,如5在合并的过程中还是在与2和1比较,只是和1的比较被规避了。
不要认为归并的过程中5只与[2,1]的数组进行了比较,事实上,在合并为[1 2 5 6]后,下一次合并中5还是会与另外一半的四个[x y z d]比较,只是比较规程中有些没必要的被规避了而已。
代码中值得注意的只有:
ans=ans+(p2-(mid+1)+1);
这代表如果p1的元素比p2大,则p1与p2前的所有元素都构成了逆序对。
class Solution {
public:
typedef long long ll;
int InversePairs(vector<int> data) {
return InversePairsCore(data,0,data.size()-1)%1000000007;
}
ll InversePairsCore(vector<int>& data,ll start,ll end)
{
if(start>=end)
return 0;
ll mid=(start+end)/2;
ll nl=InversePairsCore(data,start,mid);
ll rl=InversePairsCore(data,mid+1,end);
vector<int> tmp(end-start+1);
ll p1=mid,p2=end;
ll p3=tmp.size()-1;
ll ans=nl+rl;
while(p1>=start&&p2>=mid+1)
{
if(data[p1]>data[p2])
{
ans=ans+(p2-(mid+1)+1);
tmp[p3]=data[p1];
p1--;
p3--;
}
else{
tmp[p3]=data[p2];
p2--;
p3--;
}
}
if(p1>=start)
{
while(p3>=0)
{
tmp[p3]=data[p1];
p1--;
p3--;
}
}
if(p2>=mid+1)
{
while(p3>=0)
{
tmp[p3]=data[p2];
p2--;
p3--;
}
}
for(ll i=0;i<tmp.size();i++)
data[i+start]=tmp[i];
return ans;
}
};