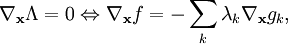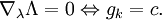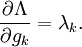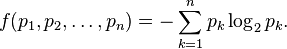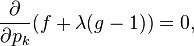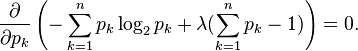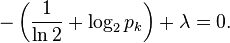在数学 最优化 问题中, 拉格朗日乘数(以 约瑟夫·路易斯·拉格朗日命名) 是一种寻找变量受一个或多个限制的多元方程的极值的方法。 这种方法将一个有n 变量与 k 约束的问题转换为一个更易解的n + k个变量的方程组,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的斜率(gradient)的线性组合里每个向量的系数。
此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。
先看一个二维的例子:假设有方程: f(x,y),要求其最大值,且
c 为常数。对不同dn的值,不难想象出
的等高线。而方程g的等高线正好是g(x,y) = c。想象我们沿着g = c的等高线走;因为大部分情况下f和g的等高线不会重合,但在有解的情况下,这两条线会相交。想象此时我们移动g= c上的点,因为f是连续的方程,我们因此能走到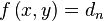 更高或更低的等高线上,也就是说dn可以变大或变小。只有当g = c和
更高或更低的等高线上,也就是说dn可以变大或变小。只有当g = c和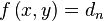 相切,也就是说,此时,我们正同时沿着g = c和
相切,也就是说,此时,我们正同时沿着g = c和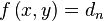 走。这种情况下,会出现极值或鞍点。
走。这种情况下,会出现极值或鞍点。
气象图中就很常出现这样的例子,当温度和气压两列等高线同时出现的时候,切点就意味着约束极值的存在。
用向量的形式来表达的话,我们说相切的性质在此意味着f和g的斜率在某点上平行。此时引入一个未知标量λ,并求解:
且 λ ≠ 0.
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
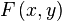 =
= 
新方程F(x,y)在达到极值时与f(x,y)相等,因为F(x,y)达到极值时g(x,y) ? c总等于零。
运用方法
如f定义为在Rn上的方程,约束为gk(x) = c(或将约束左移得到gk(x) ? c = 0)。定义拉格朗日Λ为
注意极值的条件和约束现在就都被记录到一个式子里了:
和
拉格朗日乘数常被用作表达最大增长值。原因是从式子:
中我们可以看出λk是当方程在被约束条件下,能够达到的最大增长率。 拉格朗日力学就使用到这个原理。
拉格朗日乘数法在Karush-Kuhn-Tucker最優化條件被推广。
很简单的例子
求此方程的最大值:
- f(x,y) = x2y
同时未知数满足
- x2 + y2 = 1
因为只有一个未知数的限制条件,我们只需要用一个乘数λ.
- g(x,y) = x2 + y2 - 1
- Φ(x,y,λ) = f(x,y) + λg(x,y) = x2y + λ(x2 + y2 - 1)
将所有Φ方程的偏微分设为零,得到一个方程组,最大值是以下方程组的解中的一个:
- 2xy + 2λx = 0
- x2 + 2λy = 0
- x2 + y2 - 1 = 0
另一个例子
所有概率的总和是1,因此我们得到的约束是g(p) = 1 即
可以使用拉格朗日乘数找到最高熵(概率的函数)。对于所有的k 从1 到 n, 要求
由此得到
计算出这n个等式的微分,我们得到:
这说明pi 都相等 (因为它们都只是 λ 的函数). 解出约束 ∑k pk = 1, 得到
因此,使用均匀分布可得到最大熵的值。
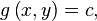
![nabla Big[f left(x, y right) + lambda left(g left(x, y right) - c right) Big] = 0](http://upload.wikimedia.org/math/4/0/6/406f930f4470f6f4e060122ab562d343.png)