本文作为自己学习李宏毅老师2021春机器学习课程所做笔记,记录自己身为入门阶段小白的学习理解,如果错漏、建议,还请各位博友不吝指教,感谢!!
Batch(批次)
首先回顾一下,在深度学习中,往往将训练数据集随机划分为N个batch,每完成一个batch的计算,便更新一次参数( heta),一轮(epoch)完成对所有N个batch的计算。在每一个epoch完成之后,对训练数据集进行shuffle,然后进行下一epoch的训练。
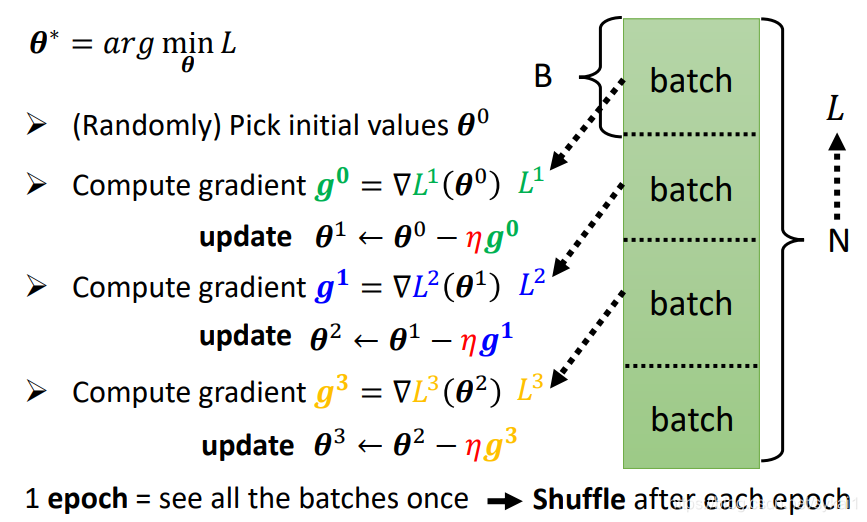
那到底选用多大的Batch size可以获得理想的训练效果呢?李宏毅老师从以下几个方面做了对比:
训练时间
以MNIST:digit classification为例: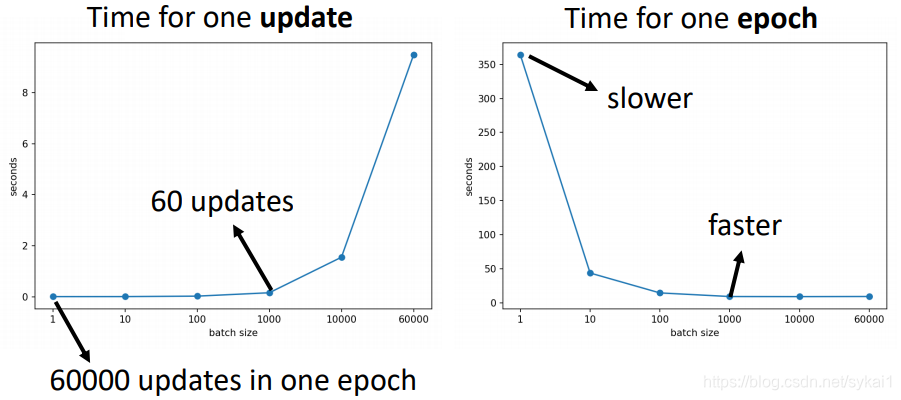
如上图所示,完成一个batch的时间,相比较来说:
- batch size越小,完成一个batch的时间越短;
- batch size越大,完成一个batch的时间越长。
如上图所示,完成一个epoch的时间,相比较来说:
- batch越小,虽然完成一个batch的时间短了,但是一个epoch中需要完成的update的次数变多,所以完成一次epoch的时间也就变长了。
- batch越大,完成一次epoch的时间越短。
训练数据集上的效果
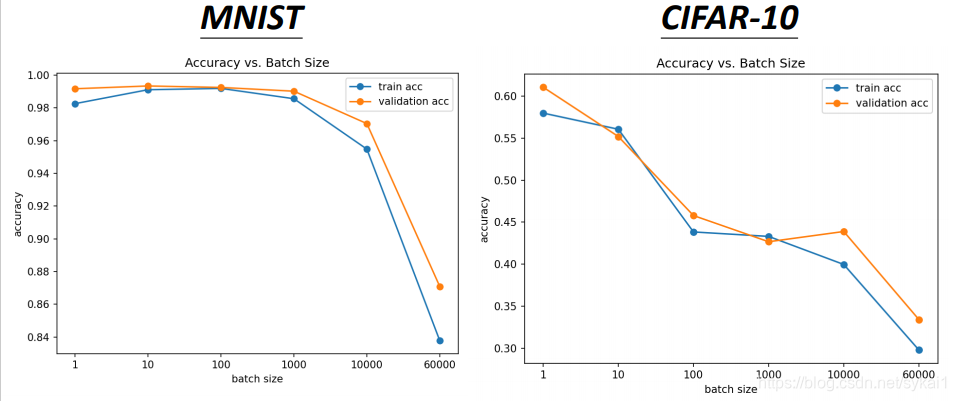
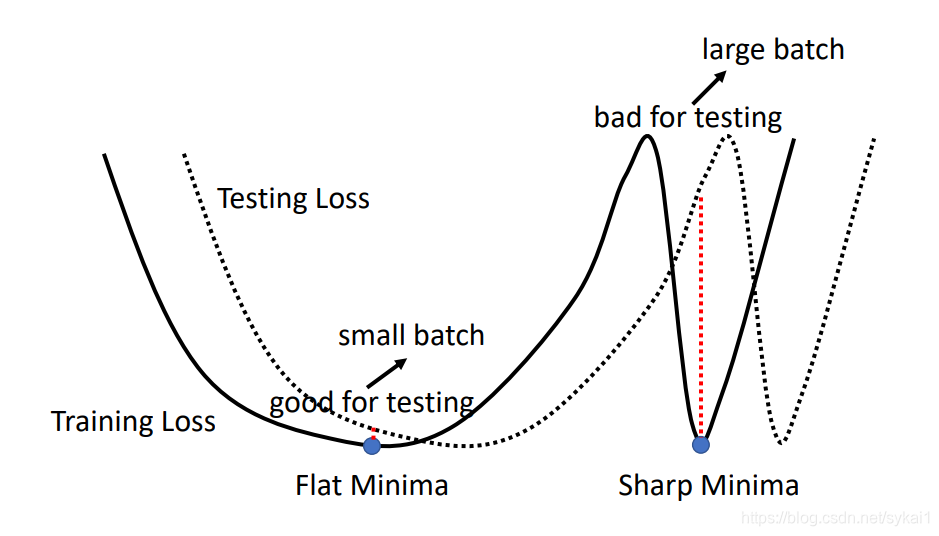
如上图所示,小的batch在训练数据集上的训练效果更好一些,而大的batch则出现了Optimization Fails问题。对这种情况的解释如下所示:
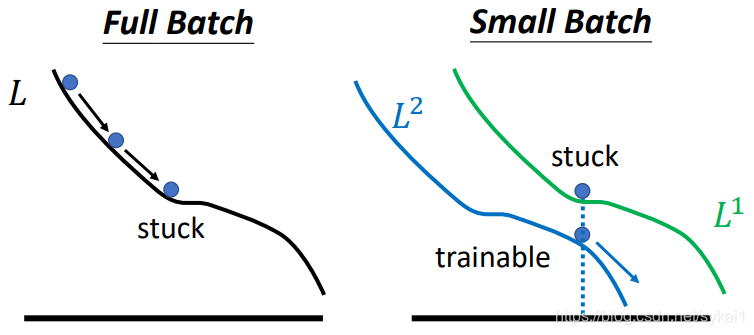
PS:Full Batch是指Batch Size = 训练数据集大小
当我们选用比较小的batch时,每次更新都是用的不同batch计算的结果,不同的batch得到的Loss是略有差异的。当在L1陷入critical point时,利用另一个batch的计算结果来更新则会更容易逃离critical point。
测试数据集上的效果
如下图所示:
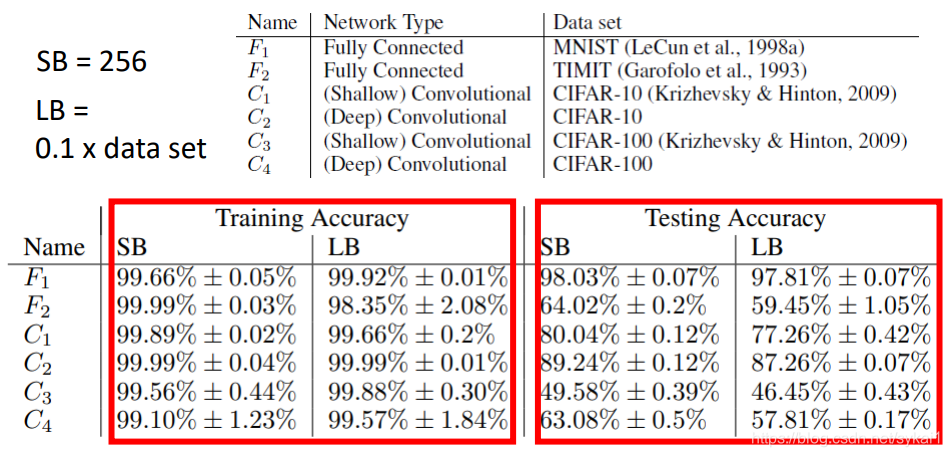
引自:
On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima(https://arxiv.org/abs/1609.04836)
从上图中可以看出,小的batch size要比大的batch size得到的模型的泛化能力要更好一些。对于这种情况的一种解释是小的batch size最终会落到平坦最小值(Flat Minima),而大的batch size最终更容易落到尖锐最小值(Sharp Minima)处。
综合来看
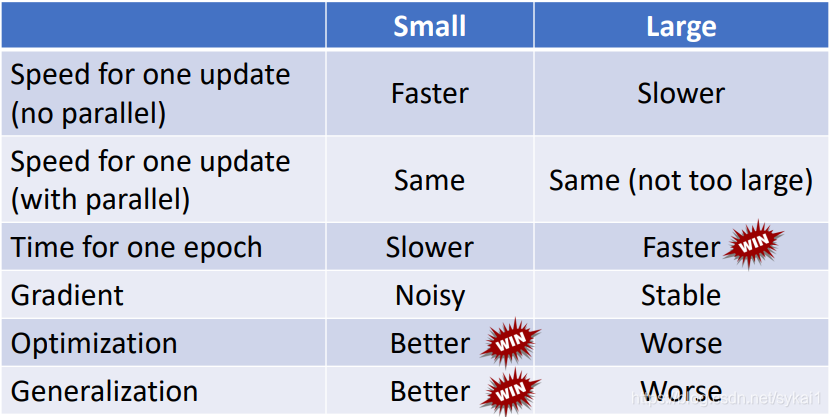
平坦最小值
深度神经网络的参数非常多,并且有一定的冗余性,这使得每单个参数对最终损失的影响都比较小,因此会导致损失函数在局部最小解附近通常是一个平坦的区域,称为平坦最小值(Flat Minima),如下图所示。
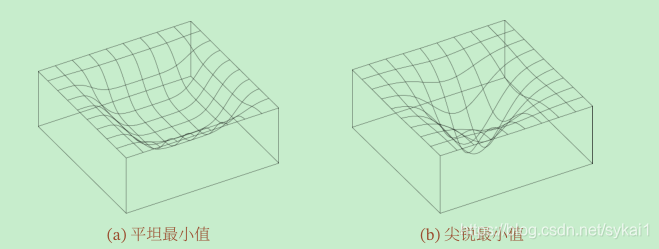
在平坦最小值的邻域内,所有点对应的训练损失都比较接近,表明我们在训练神经网络时,不需要精确的找到一个局部最小解,只要在一个局部最小解的邻域内就足够了。平坦最小值通常被认为和模型泛化能力有一定的关系。一般而言,当一个模型收敛到一个平坦的局部最小值时,其鲁棒性会更好,即微小的参数变动不会剧烈影响模型能力;而当一个模型收敛到一个尖锐的局部最小值时,其鲁棒性也会比较差。具备良好泛化能力的模型通常应该是鲁棒的,因此理想的局部最小值应该是平坦的。可以参考下图做理解:
如上图,尖锐最小解附近,Testing Loss轻微的晃动,都会对模型能力造成巨大的影响(红色虚线)。
Momentum(动量法)
在一般的梯度下降算法(Vanilla Gradient Descent)中,我们是根据计算的梯度的负方向来更新参数( heta),如下图所示:
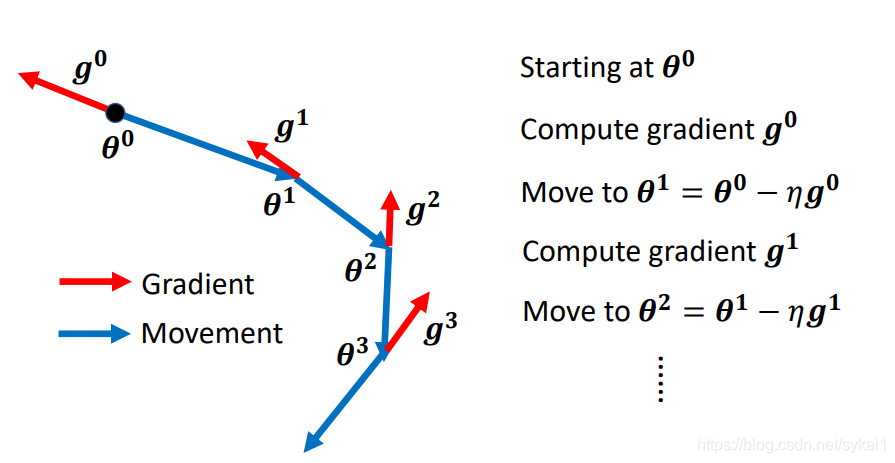
而在动量法中,则是用之前积累动量代替真正的梯度来更新参数( heta)。而动量的计算方法不仅取决于梯度,同样取决于之前的动量,其计算方法是:当前的动量 = 前一步的动量 - 当前的梯度。如下图所示:
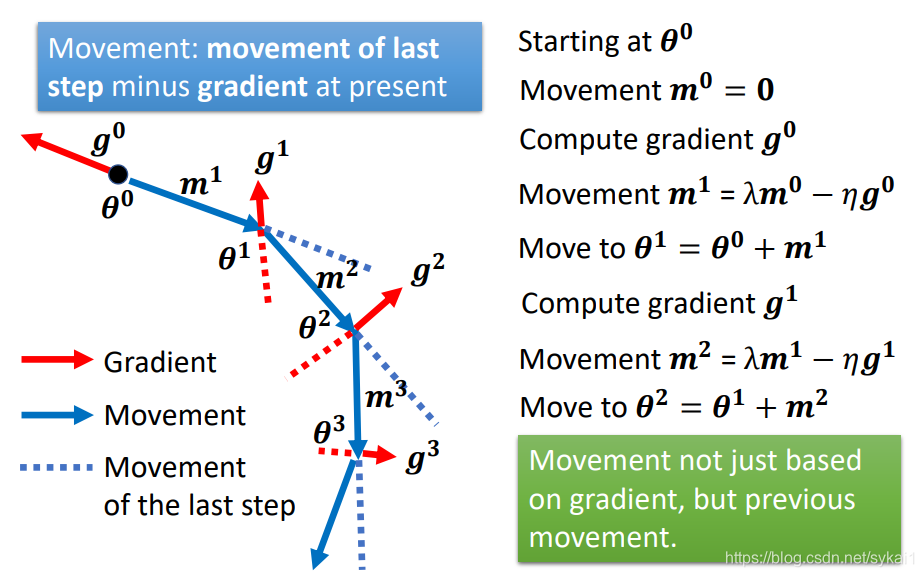
根据上图,我们将前边的动量值代入后续动量的公式中,计算出所有动量的值:
由此可见动量(m^i)是之前所有梯度(g^0,g^1,ldots,g^{i-1})的加权和,进而可以如下表示:
即
其中(lambda)为动量因子,通常设为0.9,(eta)为学习率。
这样,每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。当某个参数在最近一段时间内的梯度方向不一致时,其真实的参数更新幅度便小;相反,当在近一段时间内的梯度方向都一致时,其真实的参数更新幅度变大,起到加速作用。一般而言,在迭代初期,梯度方向都比较一致,动量法会起到加速作用,可以更快的到达最优点。在迭代后期,梯度方向会不一致,在收敛值附近震荡,动量法会起到减速作用,增加稳定性。从某种角度来说,当前梯度叠加上部分的上次梯度,一定程度上可以近似看作二阶梯度。
参考资料:
《统计学习方法(第2版)》 李航
《神经网络与深度学习》 邱锡鹏