牛顿法、拟牛顿法以及与梯度下降法的对比

牛顿法、拟牛顿法相关资料：

http://www.cnblogs.com/richqian/p/4535550.html

https://www.codelast.com/%E5%8E%9F%E5%88%9B%E6%8B%9F%E7%89%9B%E9%A1%BF%E6%B3%95quasi-newton%EF%BC%8Cdfp%E7%AE%97%E6%B3%95davidon-fletcher-powell%EF%BC%8C%E5%8F%8Abfgs%E7%AE%97%E6%B3%95broyden-fletcher-goldfarb-shanno/

http://blog.csdn.net/itplus/article/details/21896981

牛顿法为什么比梯度下降法求解需要的迭代次数更少？

牛顿法是二阶收敛（泰勒二阶展开），梯度下降是一阶收敛（泰勒一阶展开），所以牛顿法就收敛更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面(二阶精度)去拟合当前所处位置的局部曲面，而梯度下降法(一阶精度)是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

1. 牛顿法起始点不能离局部极小点太远，否则很可能不会收敛。(考虑到二阶拟合应该很容易想象)，所以实际操作中会先使用别的方法，比如梯度下降法，使更新的点离最优点比较近，再开始用牛顿法。
2. 牛顿法每次需要更新一个二阶矩阵，当维数增加的时候是非常耗内存的，所以实际使用是会用拟牛顿法。
3. 梯度下降法在非常靠近最优点时会有震荡，就是说明明离的很近了，却很难到达，因为线性的逼近非常容易一个方向过去就过了最优点(因为只能是负梯度方向)。但牛顿法因为是二次收敛就很容易到达了。

牛顿法最明显快的特点是对于二阶函数(考虑多元函数的话要在凸函数的情况下)，牛顿法能够一步到达，非常有效。

牛顿法是算当前位置的Hessian矩阵，拟牛顿法是根据最近几个迭代点的信息（包括点的位置本身和梯度）猜当前位置的Hessian矩阵。其他部分一样。

https://www.zhihu.com/question/19723347

牛顿法首先对目标函数二阶泰勒展开，然后求展开式的极值点，即可推出迭代关系：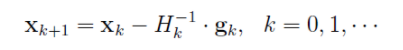

当目标函数是二次函数时，由于二阶泰勒展开式与原目标函数完全相同，hesse矩阵退化为常数，从任一初始点出发，利用上述迭代式只需一步即可达到目标函数的极小点，因此牛顿法是一种具有二次收敛性的算法，对于非二次函数，若函数的二次性较强，或迭代点已进入极小点的邻域，则其收敛速度也很快，这是牛顿法的主要优点。

牛顿法不能保证函数值稳定地下降，二阶近似展开后，函数开口方向不确定。

牛顿法存在两个缺点：

1、对目标函数有较严格的要求，函数必须具有连续的一、二阶偏导数，海森矩阵必须正定

2、计算量很大，需要计算二阶偏导数矩阵和它的逆矩阵

牛顿法每步都需计算当前位置的Hesse矩阵，拟牛顿法是通过迭代的方式来更新【Hesse矩阵或逆矩阵】的近似矩阵