生成树计数问题:给出一个无向图,求它的生成树的个数。
预备知识
(1)一个n个顶点的无向图G,定义它的度数矩阵D,D是一个n*n的矩阵。对于顶点u,设度数为deg[u],如果i=j,那么D[i][j]=deg[i],否则D[i][j]=0.
(2)一个n个顶点的无向图G,定义它的邻接矩阵A,A是一个n*n的矩阵。如果i和j之间有边,那么A[i][j]=1,否则等于0。
(3)一个n个顶点m条边的无向图G,定义它的关联矩阵B,B是一个n*m的矩阵。对于第i条边e[i]=(u,v),那么B[u][i]和B[v][i]中一个是1,一个是-1,第i列其他值为0。那么我们有
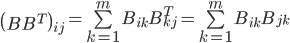
所以对于
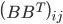
如果i=j,它是顶点i的度数,否则,如果i和j之间有边,那么它等于-1,否则它等于0.
(4)对于一个n个顶点m条边的无向图G,定义它的Kirchhoff矩阵C,C是一个n*n的矩阵,
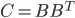
很显然,C=D-A
Matrix-Tree定理
对于一个无向图G,它的生成树个数等于其Kirchhoff矩阵任何一个n-1阶主子式的行列式的绝对值。 所谓n-1阶主子式,就是对于任意一个r,将C的第r行和第r列同表示时删去后的新矩阵,用下面的字母表示$C_{r}$
接下来,我们首先证明下面四个性质:
性质1:对于任何一个图的Kirchhoff矩阵C,它的行列式为0。
性质2:对于不连通的图,它的Kirchhoff矩阵C的任一个n-1阶主子式的行列式均为0。
性质3:如果G是一棵树,它的Kirchhoff矩阵C的任一个n-1阶主子式的行列式均为1。
性质4:柯西-比内公式。设A和B分别是n*m和m*n的矩阵,那么


其中S是一个子集,大小为n,也就是S取遍所有的n子集,相应的As和Bs为从A和B中取出S元素下标的所有列和所有行。
性质1证明:由C的性质可得,它的每一行每一列和均为0,那么我们把第2到第n行都加到第一行,那么第一行就全部是0了。有一行全部是0,那么它的行列式就是0了。
性质2证明: 假设G中存在k(k>1)个连通分量G1,G2,,,,,Gk,那么,我们可以重新安排C的行和列使得属于G1的顶点首先出现,然后是G2等。显然,行和列都要交换,所以进行了偶数次交换。所以,行列式的符号没有改变。 交换后是下面这个样子:
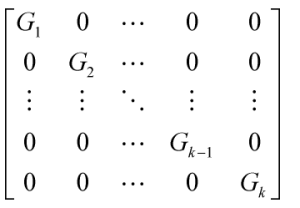
设r是Gi中的第j行,那么
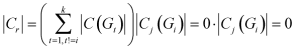
性质3证明:这里给出一个构造的方法,使得矩阵$C_{r}$通过一系列变换,成为上三角矩阵,且对角线全部是1。第一步,将r看做树根,将所有点按照距离顶点r的距离升序排序,距离相同的随便排。第二步,重新编号 n-1个顶点,距离r越近的点编号越小,Cr这个矩阵也按照重新编号后的顺序重新排列。第三步,对于以r为根的树,设j是i的父亲(父亲是r的就不用管了),那么将第i列加到第j列上。 最后我们来说明,现在的Cr是对角线为1的上三角矩阵,也就是说明对于每一列x,第x个元素下面都是0,第x个元素是1。首先最后一列即n-1列满足,因为它下面没有元素了。我们来看第x列,它的孩子所在的列都在它的后面。它的孩子,不妨设有三个a,b,c,满足了第a列第a个元素下面都是0,第a个元素是1,第b列第b个元素下面都是0,第b个元素是1,第c列第c个元素下面都是0,第c个元素是1 。而第x列第x个元素下面的第a,b,c正好都是-1,a,b,c列加过来之后变成0了,而第x个元素原来是4(除了三个孩子外,它还有父亲),而第a,b,c列的第x个元素都是-1,加过来之后就是4-3=1了。证毕。
性质4:我不会证明这个。
有了上面四条性质,来证明Matrix-tree定理:

我们看到,S枚举了所有的n-1子集,那么对于

如果S枚举的n-1子集是一个生成树,它的值为1,否则它为0。所以$det(C_{r})$就是生成树的个数。