隐马尔可夫模型-概率计算算法
上一篇博客简单介绍了隐马尔科夫模型算法的基本思想,但是没有介绍计算如何区计算它的状态转移概率矩阵,观测概率矩阵和初始状态概率向量如何计算,这节我们就来谈谈。
给出之前讲过的所有状态的集合Q,和所有可能的观测的集合V,状态序列I,和观测序列O的符号表示:
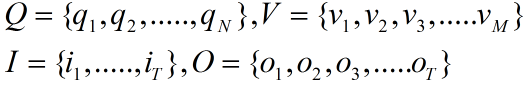
对于状态转移矩阵A和观测概率矩阵B,和初始状态概率向量C有
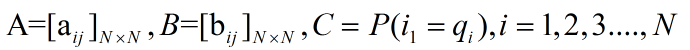
所以对于我们的问题来说,当我们得到A,B,C后,如果我们需要得到一个T的观测序列,则需要以下步骤:
- 首先需要又C来产生一个初始状态i(t),t=1
- 然后通过B得到当前状态对应的观测记过o(t)
- 然后,通过A得到下一个时间的状态i(t+1)
- 返回第二步,不断重复,直到t=T
隐马尔科夫模型有三个基本问题,也是我们在应用中最常用到的
(1)概率计算问题:给定已知的模型参数Z=(A,B,C),和观测序列O,求在模型Z条件下观测序列O出现的概率P(O|Z)
(2)学习问题,这个应该是我们碰到最多的,已知观测序列O,求模型Z=(A,B,C)使P(O|Z)最大。
(3)预测问题,也称解码问题,已知模型Z和观测序列O求给定观测序列对应最大概率的状态序列,即求最大的P(I|O)
对于第一问,我们可以采用直接计算法
直接计算法:给定模型Z和长度为T观测序列O,计算观测序列O出现的概率P(O|Z),可以求出所有可能的长度为T的状态序列I,求他们的P(O|I,Z),然后求和。
直接计算法的思路就是,整个过程是未知的,我们不知道在模型Z的限制下是哪个I产生了O,每个可能的I都是有可能产生O的,所以我们就求所有可能与O对应的I的联合概率之和。
数学公式表达如下:

我觉得上面这个计算公式明显计算量太大,是O(TN^T)阶的,如果我们的序列长度为十,序列状态集合N=20,那么我们的计算量将达到就能达到万亿的计算量。
这里在介绍一个前向算法,求解给定Z,O下的P(O|Z)

前向算法的思路就是,对于观测序列的第一个结果o(1),我们知道,他可能由所有可能的状态生成,即N个,那么我们现在如果要求在o(1)的基础上o(2)发生的概率那么不就是N可能生成o(1)的状态概率之和在生成N可能生成o(2)的状态概率之和。不断递归下去,就可以求解o(T)。