数据结构之各种树

导读

　　文本总结了数据结构中常见的各种树，前面的文章中我们介绍过树和二叉树，比如用于实现平衡二叉树的AVL树和红黑树、B树、B-树、B+树、B*树、R树及字典树Trie树。

一、平衡二叉树之AVL树

　　参考博客：https://www.cnblogs.com/QG-whz/p/5167238.html#_label1

　　学习AVL的的关键在于使用旋转操作进行失衡处理。

　　1、定义

　　AVL树是最先发明的自平衡二叉查找树。所以AVL树是一种二叉平衡树，即AVL树是二叉平衡树的一种实现。

　　ps：AVL树既然是二叉平衡树，那么必须满足：1）是二次排序树；2）左右子树相对高度差不大于1。

　　2、相关概念

　　平衡因子：将二叉树上结点的左子树高度减去右子树高度的值称为该结点的平衡因子BF(Balance Factor)。

　　最小不平衡子树：距离插入结点最近的，且以平衡因子绝对值大于1的结点为根的子树。

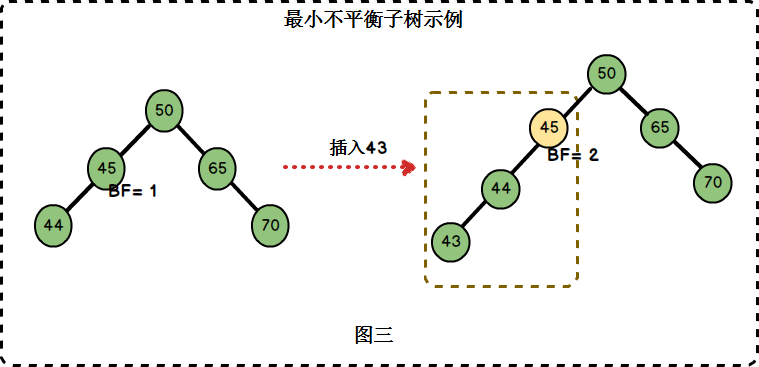
　　在图三中，左边二叉树的结点45的BF = 1，插入结点43后，结点45的BF = 2。结点45是距离插入点43最近的BF不在[-1,1]范围内的结点，因此以结点45为根的子树为最小不平衡子树。

　　3、AVL树的实现

　　1）结点结构

struct AVLTreeNode<T>
{    
    T key;//结点数据
    int height;//结点高度（用于计算父结点的平衡因子）
    AVLTreeNode<T> lchild;//左孩子指针
    AVLTreeNode<T> rchild;//右孩子指针
};

　　ps:这里结点高可以替换为平衡因子。

　　2）AVL树的抽象数据结构

template<typename T>
class AVLTree
{
public:
    AVLTree();            //构造函数
    ~AVLTree();            //析构函数
 
    void preOrder();    //前序遍历AVL树
    void InOrder();        //中序遍历AVL树   
    void postOrder();    //后序遍历AVL树
 
    void print();        //打印AVL树
    void destory();        //销毁AVL树
 
    void insert(T key);    //插入指定值的节点
    void remove(T key);    //移除指定值的节点
 
    AVLTreeNode<T>* search_recurse(T key);    //利用递归算法进行指定值的查找
    AVLTreeNode<T>* search_iterator(T key);    //利用迭代算法进行指定值的查找
    T minimum();        //返回AVL中的最小值
    T maximum();        //返回AVL中的最大值
 
    int height();        //返回树的高度
 
private:
    AVLTreeNode<T>* root;    //AVL树的根节点
 
private:
    void preOrder(AVLTreeNode<T>* pnode) const;
    void inOrder(AVLTreeNode<T>* pnode) const;
    void postOrder(AVLTreeNode<T>* pnode) const;
 
    void print(AVLTreeNode<T>* pnode,T key, int direction) const;
    void destory(AVLTreeNode<T>* & pnode);
 
    AVLTreeNode<T>* insert(AVLTreeNode<T>* &pnode, T key);       
    AVLTreeNode<T>* remove(AVLTreeNode<T>* & pnode, AVLTreeNode<T>* pdel); //删除AVL树中节点pdel，并返回被删除的节点
 
    AVLTreeNode<T>* minimum(AVLTreeNode<T>*pnode)const;
    AVLTreeNode<T>* maximum(AVLTreeNode<T>*pnode)const;
 
    AVLTreeNode<T>* search_recurse(AVLTreeNode<T>* pnode, T key) const;
    AVLTreeNode<T>* search_iterator(AVLTreeNode<T>* pnode, T key) const;
 
    AVLTreeNode<T>* leftRotation(AVLTreeNode<T>* pnode);        //单旋:左旋操作
    AVLTreeNode<T>* rightRotation(AVLTreeNode<T>* pnode);        //单旋:右旋操作
    AVLTreeNode<T>* leftRightRotation(AVLTreeNode<T>* pnode);    //双旋:先左旋后右旋操作
    AVLTreeNode<T>* rightLeftRotation(AVLTreeNode<T>* pnode);    //双旋:先右旋后左旋操作
 
};

　　4、AVL树的操作

　　AVL树具有一般二叉树的查找、插入和删除等基本操作，但AVL树作为自平衡二叉查找树，需要保证其平衡因子不大于1，而插入或删除操作都可能会打破树的平衡，所以AVL树的特殊操作是进行旋转操作，以此来调整树的不平衡子树。

　　1）旋转操作

　　为了方便说明，假设我们要为数组a[]={4，5，6，3，2，8，7，0，1}构建一棵AVL树。

　　情况一：左单旋转

　　首先插入{4，5，6}，在插入元素6后出现不平衡的情况：

　　当我们在右子树插入右孩子导致AVL失衡时，我们需要进行单左旋调整。旋转围绕最小失衡子树的根节点进行。
　　在删除新节点时也有可能会出现需要单左旋的情况。
　　左旋参考代码如下：

/*左旋转操作*/
/*pnode为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template<typename T>
AVLTreeNode<T>* AVLTree<T>::leftRotation(AVLTreeNode<T>* proot)
{
    AVLTreeNode<T>* prchild = proot->rchild;
    proot->rchild = prchild->lchild;
    prchild->lchild = proot;
 
    proot->height = max(height(proot->lchild),height(proot->rchild))+1;     //更新节点的高度值
    prchild->height = max(height(prchild->lchild), height(prchild->rchild)) + 1; //更新节点的高度值
 
    return prchild;                    
};

　　情况二：右单旋转

　　我们继续插入元素{3，2}，此时二叉树为：

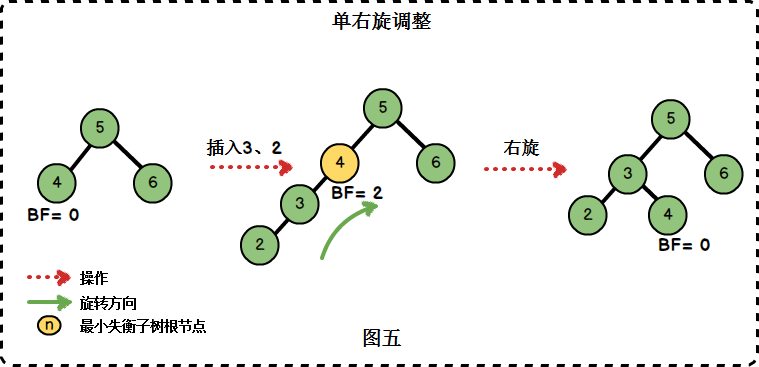
　　此时的插入情况是“在左子树上插入左孩子导致AVL树失衡”，我们需要进行单右旋调整。
　单右旋参考代码为：

/*右旋转操作*/
/*pnode为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template <typename  T>
AVLTreeNode<T>* AVLTree<T>::rightRotation(AVLTreeNode<T>*proot)
{
    AVLTreeNode<T>* plchild = proot->lchild;
    proot->lchild = plchild->rchild;
    plchild->rchild = proot;
 
    proot->height = max(height(proot->lchild), height(proot->rchild)) + 1;     //更新节点的高度值
    plchild->height = max(height(plchild->lchild), height(plchild->rchild)) + 1; //更新节点的高度值
 
    return plchild;
};

　　情况三：先左旋后右旋

　　需要进行两次旋转的原因是第一次旋转后，AVL树仍旧处于不平衡的状态，第二次旋转再次进行调整。
　　我们继续插入元素{8，7}：

　　这种情况，总结起来就是“在右子树上插入左孩子导致AVL树失衡",此时我们需要进行先右旋后左旋的调整。

　　情况四：先左旋后右旋

　　根据对称性原理，当我们“在左子树上插入右孩子导致AVL树失衡",此时我们需要进行先左旋后右旋的调整。如果你不理解接着看图。
　　我们接着插入节点{0，1}：

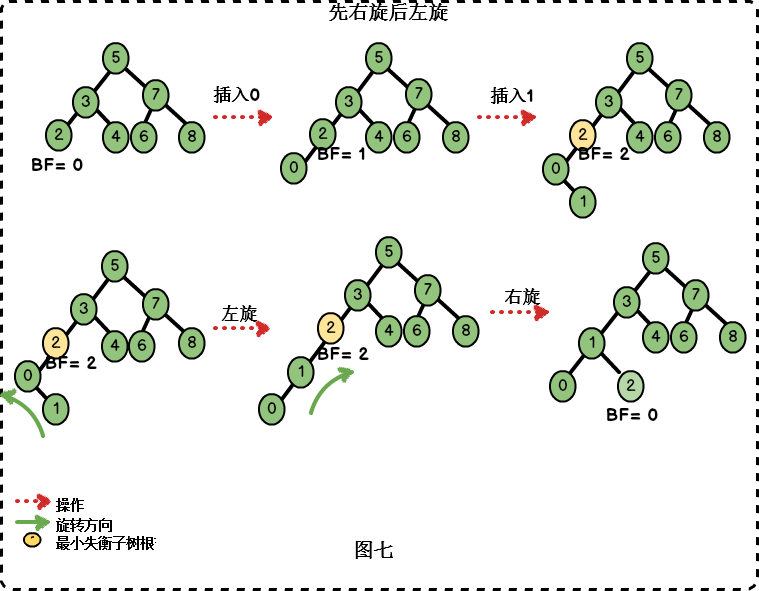
　　总结：四种失衡调整

　　2）其他操作

　　其他操作如插入、删除、查找、遍历与一般二叉树的操作类似，不同之处在于如果插入或删除操作导致树失衡，需要进行旋转操作进行恢复平衡。