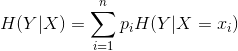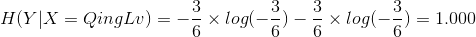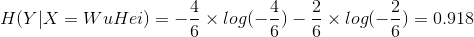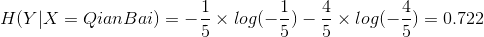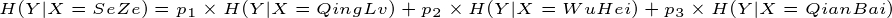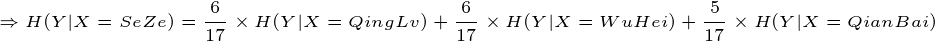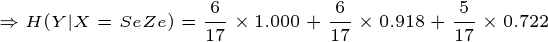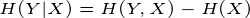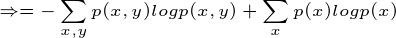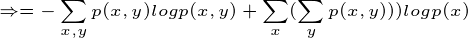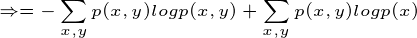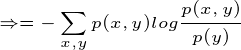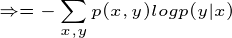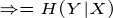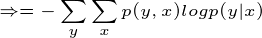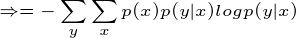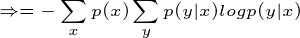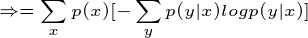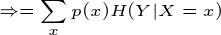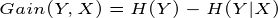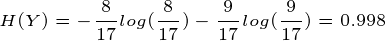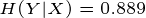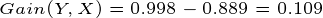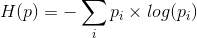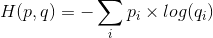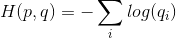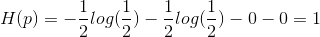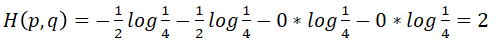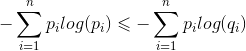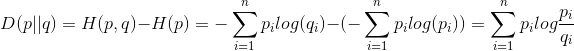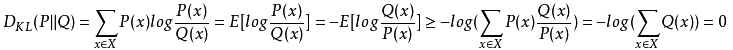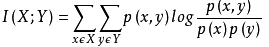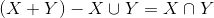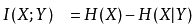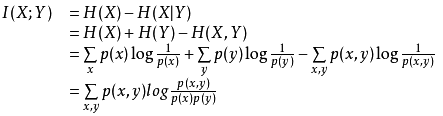条件熵:
H(Y|X)表示在已知随机变量X的条件下,随机变量Y的不确定性,H(Y|X)定义为:
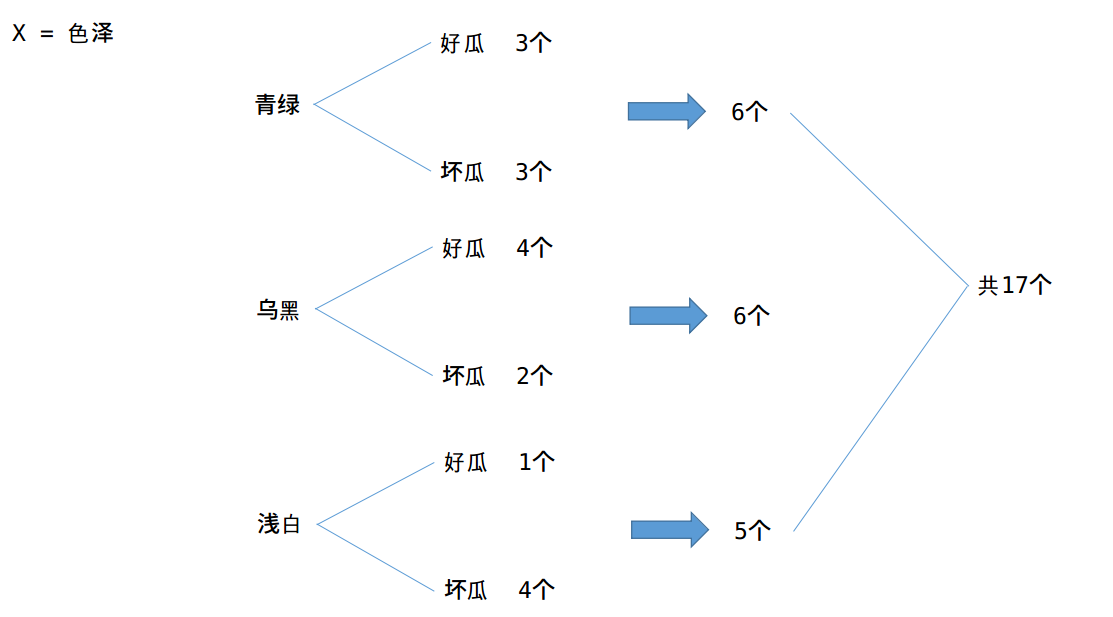
举个例子: 有一堆西瓜,已知这堆西瓜的色泽,以及每种色泽对应好瓜和坏瓜的个数,如下所示,设X表示色泽,Y表示好瓜或者坏瓜。
则:
这个例子就是计算条件熵的一个过程,现在证明条件熵公式:
有很多书上的条件熵是这么定义的,如果继续化简就可以得到我们上面定义的条件熵,接着化简:
得证!
信息增益:
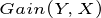
比如上述西瓜的例中,当不知道色泽的时候,好瓜与坏瓜的不确定度为:
当知道色泽之后,好瓜与坏瓜的不确定度为:
那么知道色泽之后,好瓜与坏瓜的不确定度减少了:
交叉熵(只谈论离散情况)
假设有这样一个样本集,p为它的真实分布,q为它的估计分布。如果按照真实分布p来度量识别一个样本所需要的编码长度的期望为:(如果对编码长度不了解的,请看:http://blog.csdn.net/hearthougan/article/details/77774948
如果使用估计的分布q来表示来自真实分布p的平均编码长度,则:
因为我们编码的样本来自于真实的分布p,所以乘的是真实概率。在图像分类的时候,比如softmax分类器,在训练的时候,我们已经给定图像的标签,所以这个时候每幅图片的真实概率就是1,这个时候的损失函数就是:
怎么理解呢?就是让预测的概率值越来越接近于1!(想多了解softmax,请参考http://blog.csdn.net/hearthougan/article/details/71629657)
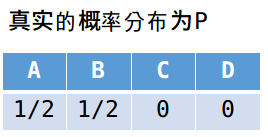
举个知乎上的例子,有4个字母(A,B,C,D)的数据集中,真实分布p=(1/2, 1/2, 0, 0),即A和B出现的概率均为1/2,C和D出现的概率都为0,
真实分布的编码长度(最优编码长度)
也就是说,我们仅仅需要一位编码就可以确定所要发送的数据是什么。那么假如我们的估计分布如下:
那么发送数据的平均编码长度为:
即为了确定所发送的数据,平均需要长度2编码,才可以。交叉熵可以这么理解:用估计的分布对来自真实分布的样本进行编码,所需要的平均长度。
根据Gibbs' inequality可知交叉熵要大于等于真实分布的信息熵(最优编码)。Gibbs' inequality如下:
对于样本服从分布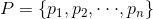
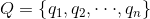
当且仅当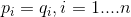
相对熵(KL散度)
由交叉熵可知,用估计的概率分布所需的编码长度,比真实分布的编码长,但是长多少呢?这个就需要另一个度量,相对熵,也称KL散度。
相对熵:用交叉熵减去真实分布的信息熵,表示用估计分布计算的平均编码长度比最短平均编码长度长多少。因此有:
交叉熵=信息熵+相对熵
由于对数函数时凸函数,则有:
因此,相对熵始终是大于等于0的。从上面的描述中也可以看得出,相对熵其实可以理解成两种分布的距离。
互信息:
两个随机变量X,Y的互信息,定义为:X,Y的联合分布P(X,Y)与乘积分布P(X)P(Y)的相对熵:
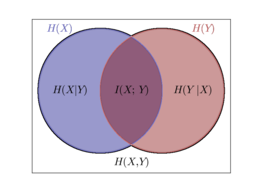
怎么理解呢?也就是用乘积分布P(X)P(Y)的交叉熵,减去联合分布的信息熵,就是互信息,还不好理解,就可以看如下图示:
相当于一种不严谨的说法就是:
或许另一种等价的定义好理解:
其实两种定义是等价的:
Reference:
https://baike.baidu.com/item/%E7%9B%B8%E5%AF%B9%E7%86%B5/4233536?fr=aladdin
https://baike.baidu.com/item/%E4%BA%92%E4%BF%A1%E6%81%AF/7423853?fr=aladdin
https://www.zhihu.com/question/41252833
--------------------- 作者:hearthougan 来源:CSDN 原文:https://blog.csdn.net/Hearthougan/article/details/77879784 版权声明:本文为博主原创文章,转载请附上博文链接!