盲信号分离

盲信号分离涉及到的相关概念

1、盲信号分离指的是从多个观测到的混合信号中分析出没有观测的原始信号。通常观测到的混合信号来自多个传感器的输出，并且传感器的输出信号独立性（线性不相关）。盲信号的“盲”字强调了两点：1)原始信号并不知道；2)对于信号混合的方法也不知道。在大多数的研究中 ,只讨论线性混合模型，当混合模型为非线性时 ,一般是无法从混合数据中恢复源信号的 ,除非对信号和混合模型有进一步的先验知识可资利用. 

2、算法做出了如下的假定：

  • 具有m个独立的信号源{displaystyle s_{1}(t),...,s_{m}(t)}和n个独立的观察量{displaystyle x_{1}(t),...,x_{n}(t)},观察量和信号源具有如下的关系{displaystyle mathbf {x} (t)=Amathbf {s} (t)}，式子的含义是 m 个源信号通过 混合得到 n维观测数据向量。其中{displaystyle mathbf {x} (t)={[x_{1}(t),...,x_{n}(t)]}^{T}},其元素是各个传感器得到的输出；{displaystyle mathbf {s} (t)={[s_{1}(t),...,s_{m}(t)]}^{T}},A是一个{displaystyle {n} imes {m}}的系数矩阵，其元素表示信号的混合情况，原问题变成了已知{displaystyle mathbf {x} (t)}和{displaystyle mathbf {s} (t)}的独立性，求对{displaystyle mathbf {s} (t)}的估计问题。
  • 假定有如下盲信号分离问题的提法是 :在 混合矩阵 A 和源信号未知的情况下 ,只根据观测数据向量 x ( t) 确定分离矩阵 W ,使得变换后的输出 y( t) = Wx ( t)  是源信号向量 s ( t) 的拷贝或估计,W是一个{displaystyle {m} imes {n}}系数矩阵，问题变成了如何有效的对矩阵W做出估计。

3、算法中涉及到的基本假设：

  • 各源信号{displaystyle s_{i}(t)}均为零均值信号，实随机变量，信号之间统计独立。如果源信号{displaystyle s_{i}(t)}的概率密度为{displaystyle p_{i}(s_{i})},则s(t)的概率密度为:{displaystyle p(s)=prod _{i=1}^{n}p_{i}(s_{i})}
  • 源信号数目m小于等于观察信号数目n，即{displaystyle m<=n}。混合矩阵A是一个{displaystyle n imes {m}}的矩阵。假定A满秩。
  • 源信号中只允许有一个高斯分布，当多于一个高斯分布时，源信号变得不可分。

4、盲信号分离存在两种不确定性或模糊性 :分离后信号顺序排列和复振幅(幅值和初始相位) 的不确定性. 盲信号分离的不确定性主要表现为混合矩阵 A 的非完全辨识. 

5、定义 1 　两个矩阵 M 和 N 称为本质相等 ,并记作 N ,若存在一矩阵 G 使得 , 其中 G 是一广义交换矩阵 ,并且其元素具有单位模。根据定义1盲信号分离问题也可叙述为 :只根据传感器输出x ( t) 辨识混合矩阵 A 的本质相等矩阵与/ 或恢复源信号.

6、文献[1]证明了信号的盲可分离性 :对于各个元素相互独立 ,并且只有一个高斯分量的信号向量 s 而言 ,若 y = Cs (其中 C 是一任意可逆矩阵) 的元素相互独立 ,则 y 是 s 的一个拷贝.

7、对信号分量 si( t) , 归一化峰度定义为，对于高斯信号 ,其归一化峰度等于零. 若 > 0 , 则称si ( t) 为超高斯信号 ;若 < 0 , 则 si( t) 为亚高斯信号。

8、定义2   令 A = A ( x) 是混合矩阵 A 的某个批处理估计器. 若对任意可逆矩阵 M 恒有A ( Mx) = M A ( x) 则称估计器 A 是等变化的 ,且称作等变化条件.等变化条件另一种表述方式：令 W ( t) 是一盲信号分离算法求得的分离矩阵 ,且 C(t) = W(t)A 是分离与混合的合成系统 ,则算法是等变化的 ,若 C( t) 满足

,式中 H( C( t) s ( t) ) 是矩阵乘积 C ( t) s ( t) 的矩阵函数 ,它与混合矩阵 A 和分离矩阵 W( t) 无关.

9、假定源信号的估计为 s ( t) = A- 1X( t) , 其中 A = A(x)是混合矩阵 A 的等变化估计器 ,则容易证明,即如果信号分离算法具有等变化性 ,则该算法的信号分离性能与混合矩阵(即信号传输的信道) 完全无关 ,只决定于原始信号 ,这一性能称为均匀性能. 

10、盲信号分离已有许多的算法 ,这些算法大致可分为以下三类（后两种方法等价） :

  • 信号经过变换后 ,使不同信号分量之间的相依性 ( de2pendency) 最小化. 这类方法称为独立分量分析 ,由 Comon 于1994 年提出.
  • 利用非线性传递函数对输出进行变换 ,使得输出分布包含在一个有限的超立方体中;然后熵的最大化将迫使输出尽可能在超立方体中均匀散布. 这类方法称为熵最大化方法 ,是 Bell 与 Sejnowski 于 1995 年提出的.
  • 非线性主分量分析是线性主分量分析方法的推广 , 由Oja 与 Karhumen 等人于 1994 年提出.

独立分量分析

1、独立分量分析( ICA) 的基本目的就是确定线性变换矩阵 W ,使得变换后的输出分量 yi( t) 尽可能统计独立.

2、定义 3 　输出向量 y 的对比函数记作 ,定义为将 y的概率密度分布集合映射为一实值函数的算子 ,并且映射函数满足下列条件 :(1) 若向量 y 的元素 yi改变排列位置 ,则函数保持不变 ,即对所有交换矩阵 P 恒有 ;(2) 若 y 的元素 yi改变“尺度”时函数保持不变 ,即对所有可逆对角矩阵 D 恒有 .

3、几种典型的独立分量分析算法：

  • 随机梯度算法 ：用瞬时或随机梯度代替式 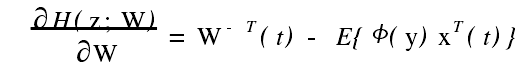的真实梯度 ,即得到由 Bell 和 Sejnoeski提出的随机梯度算法为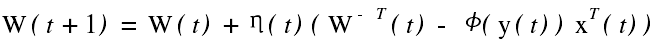式中η(t) 为学习速率或步长. 这一算法的主要缺点是 :收敛速度慢 ,同时由于涉及分离矩阵 W( t) 的求逆 ,一旦 W ( t) 在更新过程中条件数变差 ,算法就可能发散. 

自然梯度算法 :当式 中的随机梯度用自然梯度代替后 ,即得自然梯度算法如下 :W ( t + 1) = W ( t) +η( t) ( I - <( y( t) ) yT( t) ) W ( t) (17)式中 ,非线性变换函数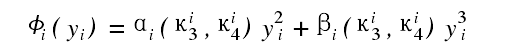

这里κi3= E{ y3i , k} 及 κi4= E{ y4i , k} - 3 分别表示 yi的偏度和峰度 ,而ai (κi3,κi4) = -12κi3+94κi3κi4(19 a)βi(κi3,κi4) = -16κi4+32(κi3)2+34(κi4)2(19 b)偏度和峰度用下面的公式更新 :κi3 , k + 1=κi3 , k- u·T·(κi3 , k- y3i , k) (20)κi4 , k + 1=κi4 , k- u·T·(κi4 , k- y4i , k+ 3) (21)自然梯度算法最早是 Cichocki 等人 1994 年提出的[13 ], 后来 Amari 等人[2 ,3 ,48 ]从理论上证明了它的有效性.(3) EASI 算法 :1996 年 ,Cardoso 和 Laheld[9 ]

非线性主分量分析

 【1】Cao X R ,Liu R W. A general approach to blind source separation [J ] .IEEE Trans. Signal Processing ,1996 ,44 :562 - 571.

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/yjh123/p/11587191.html