求三角函数的最值

前言

对三角函数求最值的几种常见考查方向整理归纳，重点说明新考向的解法思路。

预备知识

数学常识：(1pm sinxge 0)；(1pm cosxge 0)；(2pm sinx> 0)；
三角变换，
二次型，配方法
解三角不等式，解三角不等式

常见考向

1、利用化一法转化为正(余)弦型函数求最值

逆用二倍角的正弦公式，二倍角的余弦公式，辅助角公式，转化为正弦型函数；

例题当(xin [-cfrac{pi}{3}，cfrac{pi}{4}])时，求函数(f(x)=2sinxcdot cosx+2sqrt{3}cdot cos^2x-sqrt{3}+1)的值域，

解析：函数(f(x)=2sinxcdot cosx+2sqrt{3}cdot cos^2x-sqrt{3}+1)

(=2sin(2x+cfrac{pi}{3})+1)

若(xin [-cfrac{pi}{3}，cfrac{pi}{4}])，则可得

(-cfrac{2pi}{3}leq 2xleq cfrac{pi}{2})，则(-cfrac{pi}{3}leq 2x+cfrac{pi}{3}leq cfrac{5pi}{6})，

故当(2x+cfrac{pi}{3}=-cfrac{pi}{3})，即(x=-cfrac{pi}{3})时，(f(x)_{min}=f(-cfrac{pi}{3})=2 imes (-cfrac{sqrt{3}}{2})+1=-sqrt{3}+1)；

故当(2x+cfrac{pi}{3}=cfrac{pi}{2})，即(x=cfrac{pi}{12})时，(f(x)_{max}=f(cfrac{pi}{12})=2 imes 1+1=3)；

例2【2017(cdot)广东汕头一模】【求面积的最大值】已知(Delta ABC)的内角(A，B，C)的对边分别是(a，b，c)，且满足(b=c)，(cfrac{b}{a}=cfrac{1-cosB}{cosA})，若点(O)是(Delta ABC)外的一点，(angle AOB= heta(0< heta<pi))，(OA=2)，(OB=1)，则四边形(OACB)面积的最大值是【】

$A.cfrac{4+5sqrt{3}}{4}$ $B.cfrac{8+5sqrt{3}}{4}$ $C.3$ $D.cfrac{4+5sqrt{3}}{4}$

分析：由(cfrac{b}{a}=cfrac{sinB}{sinA}=cfrac{1-cosB}{cosA})，

得到(sinBcosA+cosBsinA=sinA)，即(sin(A+B)=sinA)

则(sinC=sinA)，即(A=C)，

故(a=b=c)，为等边三角形。

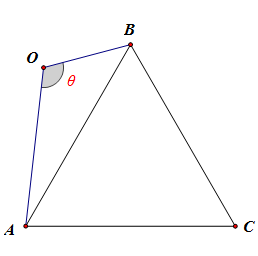
在(Delta AOB)中，(AB^2=2^2+1^2-2cdot 2cdot 1cdot cos heta=5-4cos heta)，

故(S_{OACB}=S_{Delta AOB}+S_{Delta ABC})

(=cfrac{1}{2}cdot 2cdot 1cdot sin heta+cfrac{sqrt{3}}{4}cdot AB^2)

(=sin heta+cfrac{sqrt{3}}{4}(5-4cos heta)=2sin( heta-cfrac{pi}{3})+cfrac{5sqrt{3}}{4})

当( heta-cfrac{pi}{3}=cfrac{pi}{2})时，即( heta=cfrac{5pi}{6}in (0，pi))时，四边形的面积有最大值，

且(S_{max}=2+cfrac{5sqrt{3}}{4}=cfrac{8+5sqrt{3}}{4})，故选(B)。

2、利用二次型函数求最值

利用配方法转化为以(sinx)或(cosx)为元的二次型函数，

高考题(2017高考真题理科全国卷2的第14题)函数(f(x)=sin^2x+sqrt{3}cosx-cfrac{3}{4}(xin[0，cfrac{pi}{2}]))的最大值为_______。

分析：由于(xin[0，cfrac{pi}{2}])，则(cosxin [0，1])，

令(cosx=tin [0，1])，(f(x)=1-cos^2x+sqrt{3}cosx-cfrac{3}{4}=1-t^2+sqrt{3}t-cfrac{3}{4}=-(t-cfrac{sqrt{3}}{2})^2+1=g(t))，

故当(t=cfrac{sqrt{3}}{2})时，(g(t)_{max}=f(x)_{max}=1)。

3、利用换元法转化为二次函数或其他函数求解

①求(f(x)=sinxpm cosxpm sinxcdot cosx)的值域问题。

②求函数(y=g(x)=cfrac{sinalphacdot cosalpha}{sinalpha+cosalpha}，alphain [0，cfrac{pi}{2}])的值域问题。

分析：令(sinalpha+cosalpha=t=sqrt{2}sin(alpha+cfrac{pi}{4})in [1，sqrt{2}])，

则(sinalphacdot cosalpha=cfrac{t^2-1}{2})，

则原函数转化为(y=g(x)=cfrac{frac{1}{2}(t^2-1)}{t}=cfrac{1}{2}(t-cfrac{1}{t})，tin [1，sqrt{2}])单调递增；

则(y_{min}=g(1)=0)，(y_{max}=g(sqrt{2})=cfrac{sqrt{2}}{4})，

4、利用均值不等式求最值

5【2019届高三理科数学三轮模拟试题】已知( riangle ABC)的内角(A)，(B)，(C)所对的边分别为(a)，(b)，(c)，且(acosC-ccosA=cfrac{3}{5}b)，则(tan(A-C))的最大值为________。

分析：首先边化角得到，(sinAcosC-cosAsinC=cfrac{3}{5}sinB)，即(5(sinAcosC-cosAsinC)=3sin(A+C))，

打开整理得到，(2sinA cosC=8cosAsinC)，弦化切得到(tanA=4tanC)，

则(tan(A-C)=cfrac{tanA-tanC}{1+tanAtanC}=cfrac{3tanC}{1+4tan^2C}=cfrac{3}{cfrac{1}{tanC}+4tanC})

(leq cfrac{3}{2sqrt{4}}=cfrac{3}{4})，当且仅当(cfrac{1}{tanC}=4tanC)时，即(tanC=cfrac{1}{2})时取到等号。

故(tan(A-C))的最大值为(cfrac{3}{4})。

5、小众考向

①求函数(y=cfrac{sinx-2}{2+sinx})的值域；

②函数(y=cfrac{cosx-2}{2+sinx})的值域；

新题补充

例5【2019信息题】函数(y=sinxcdot cos^2x)的最大值为____________。

提示：令(sinx=tin [-1，1])，则原函数转化为(y=t(1-t^2))，(t in [-1，1])，(y_{max}=cfrac{3sqrt{2}}{9})；

法2：尝试可否直接求导；

例6【2019学生问题】[转化划归+恒成立问题+分离参数+换元法+求最值]

函数(f(x)=cos2x+a(sinx-cosx))在区间([0，cfrac{pi}{2}])上单调递增，求实数(a)的取值范围。

分析：由于函数(f(x)=cos2x+a(sinx-cosx))在区间([0，cfrac{pi}{2}])上单调递增，

则(f'(x)ge 0)在区间([0，cfrac{pi}{2}])上恒成立，

又(f'(x)=-2sin2x+a(cosx+sinx)ge 0)在区间([0，cfrac{pi}{2}])上恒成立，

由于(xin [0，cfrac{pi}{2}])，(cosx+sinx>0)，故用完全分离参数法，得到，

(age cfrac{2sin2x}{sinx+cosx})在区间([0，cfrac{pi}{2}])上恒成立，

题目转化为求函数(g(x)=cfrac{2sin2x}{sinx+cosx})的最大值问题。

令(sinx+cosx=t=sqrt{2}sin(x+cfrac{pi}{4}))，则(tin [1，sqrt{2}])，

则(sin2x=t^2-1)，则函数(g(x)=h(t)=cfrac{2(t^2-1)}{t}=2(t-cfrac{1}{t}))，

又函数(h'(t)=1+cfrac{1}{t^2}>0)在(tin [1，sqrt{2}])上恒成立，

故函数(h(t))在(tin [1，sqrt{2}])上单调递增，

故(g(x)_{max}=h(t)_{max}=h(sqrt{2})=sqrt{2})，

故(age sqrt{2})。即(ain [sqrt{2}，+infty))。