动态规划
DP和前几天学的东西不大一样，动态规划和数据结构相比是一个非常抽象的东西
先来看看斐波那契数列
定义是F0=0，F1=1，Fn=F(n-1)+F(n-2)
0,1,1,2,3,5,8,13，这个数列的定义域是零到正无穷，他有一个边界条件就是F0=0，F1=1，
我们把这个固定的值叫做边界条件
而看一看Fn=F(n-1)+F(n-2)，会发现Fn的值是依赖F(n-1)和F(n-2)的，所以这些就不是边界条件，也就是说，边界条件是不需要计算其他斐波那契数列的值就能得到的
Fn=F(n-1)+F(n-2)这个东西我们叫他动态规划的的转移方程，就是我们如何用已有的状态转移出未知的状态的方法
我们把F 0 F1 F2 F3.... Fn叫做状态，
动态规划还有一个东西叫做 无后效性 ，它等价于有向无环图（DAG）实际上对于任何的DP题，我们只需要确定状态，边界条件和转移方程，这个题就完事了
动态规划一共有三种写法，：顺着推，倒着推，记忆化搜索
顺着推（递推）
我们定义了一个数组f[N]，然后写出状态的边界条件
cin >> n;
f[0] = 0;
f[1] = 1;
cin >> n;
f[0] = 0;
f[1] = 1;
for (int a = 1; a < n; ++a)
{
f[a + 1] += f[a];
f[a + 2] += f[a];
}
这个时候我们去考虑F[a]已经被算出来了，关键就是看F[a]对于其他的状态有什么贡献，我们就是一个一个加上去就可以了，我们主要是用F[a]更新F[a+1]和 F[a+2]的值（用自己来更新别人）
逆着推（感觉这个更常用）（递归）
处理和上面相同
，然后直接按照状态转移方程来写就行了（用别人来更新自己）
for (int a = 1; a < n; ++a)
f[a] += f[a - 1] + f[a - 2];
虽然在这个题里头这俩没什么差别，但是在个别BT题目里头·1，如果用错了，可能会让时间复杂度*N之类的，就T了
记忆化搜索
int dfs(int n)
{
if(n==0) return 0;
if(n==1)return 1;
return dfs(n-1)+dfs(n-2);
}
int main()
{
cin>>n;
cout<<dfs(n)<<endl;
return 0;
}
这个只是一个非常垃圾的搜索，时间复杂度是O( f(n) )的，也就是复杂度和斐波那契数列的大小是成正比的，因为我们能知道他的通项公式是
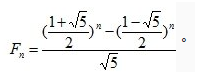
这样的话时间复杂度就是一个指数级别的，那肯定很慢，那么为什么慢？
是因为我们在算F(n)的时候，我们要算F(n-1)和F(n-2)，但是我们在算F(n-1)就已经把F(n-2)算过一遍了，其他的值也都是这个道理，所以造成了很大的时间浪费，因此我们试一试记忆化搜索，我们只要保证从F0到Fn-1里面的每一个数只被算一次，这个就叫记忆化搜索，这里我们开两个数组
一个用来存储第i项斐波那契数列的值，另一个用来存储斐波那契第i项有没有被算过
int dfs(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (suan_le_mei[n])
return f[n];
suan_le_mei[n] = true;
f[n] = dfs(n - 1) + dfs(n - 2);
return f[n];
}
一看那个数组名字也知道它的目的了吧（大雾）
这样就能保证每一个值只被算过了，这样写的时候，就能和上面那俩方法的复杂度一样了是O(n)
矩阵优化的时间复杂度是O(logn)简直是神奇
正式进入DP环节了
数位DP
树形DP
状压DP
区间DP
其他DP（NOIP出现可能性最大的？？？？？？？什么鬼）
还有两个NOIP当中多半不会考的玄学DP，插头DP和博弈论DP
来看吧
数位DP
例一
读入两个正整数L,R，问从L到R有多少个数，答案就是L-R+1，这肯定是没有什么挑战性啊是吧，为了挑战自己，我们用一下数位DP（大雾）
我们能知道L~R的数就是0~R的个数减去0~（L-1）这段数的个数
转移了之后，我们就只需要求0-X这段数的个数。
我们可以把X的十进制写出来，他们分别是Xn Xn-1 .....X1 X0（X0是个位）
问题就.转化成了找所有的v满足0<=v<=x
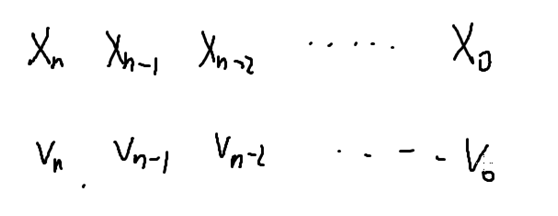
我们考虑给下面这一行v每一位填上一个数，看有多少情况满足条件就可以了，因为我们从高位开始填，所以我们填Vi的时候，它前面的所有数位都已经被填了，那么Vi能填什么呢，我们得分类讨论，他前面的数有两种情况，一种是正好和X的前i位相等，这个时候我们就只能填0-Xi这些数，当比X小的时候，我们就可以填0-9十个数字了
一般来说数位DP的状态有两个维度F[i][j]
i表示已经填到了第i位
j是0或1，表示到底是等于x的前i位还是小于x的前i位
状态转移的话就是枚举第i-1位填什么（不要忘了i是递减的），然后就转移到F[i-1][j’]上，这就是数位DP的核心思想
来看代码
int solve(int x)
{
int n=0;
while(x)
{
z[n]=x%10;
x/=10;
n++;
}
n--;
memset(f,0,sizeof(f));
f[n+1][1]=1;
for(int a=n;a>=0;a--)
{
for(int b=0;b<=1;b++)
{
if(b==0)
{
for(int c=0;c<=9;c++)
f[a][0]+=f[a+1][b];
}
else
{
for(int c=0;c<=z[a];c++)
{
if(c==z[a]) f[a][1]+=f[a+1][b];
else f[a][0]+=f[a+1][b];
}
}
}
}
return f[0][0]+f[0][1];
}
int main()
{
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<endl;
return 0;
}
因为我们实际上是求0~R和0~（L-1）这两端数，填第n位的时候是从第n+1位转移过来的
就是求0—x的十进制表示存下来
为什么要清空呢
边界条件就是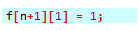
也就是二者都填0
最后我们把小于的方案加上等于的方案，就是最终结果了
例二
求在[l,r]中的数的数位之和
这里肯定是可以用数学方法做，但是我们考虑用DP，我们在这里多加入一个条件
int l,r,z;
int f[23333][2];
int g[23333][2];
int solve(int x)
{
int n=0;
while(x)
{
z[n]=x%10;
x/=10;
n++;
}
n--;
memset(f,0,sizeof(f));
memeste(g,0,sizeof(g));
f[n+1][1]=1;
g[n+1][1]=0;//因为第n+1位是0
for(int a=n;a>=0;a--)
{
for(int b=0;b<=1;b++)
{
if(b==0)
{
for(int c=0;c<=9;c++)
{
f[a][0]+=f[a+1][b];//每一个方案对数位之和贡献一个c
g[a][0]+=g[a+1][b]+f[a+1][b]*c;
}
}
else
{
for(int c=0;c<=z[a];c++)
{
if(c==z[a])
{
f[a][1]+=f[a+1][b];
g[a][1]+=g[a+1][b]+f[a+1][b]*c;
}
else
{
f[a][0]+=f[a+1][b];
g[a][0]+=g[a+1][b]+f[a+1][b]*c;
}
}
}
}
}
return g[0][0]+g[0][1];
}
int main()
{
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<endl;
return 0;
}
例三
求在[l,r]中满足十进制位中相邻两个数字之差至少为2的数有多少个
我们增加一个状态[k]，表示第i位填的是k，和上面的题目解法差不多，我们只需要保证第i位和第i+1位的差至少为2就可以
树形DP
给你n个点，问你树总共有几个点？？？？？？？
这个更弱智啊，但是我们还是得做。。。。。
用树形DP吧
存一下树，主要就是找找儿子什么的，我们知道一个点的子树大小，是他所有儿子的字数大小
加起来再加1（还有其本身），当我们一个一个加起来加到根节点就能得到答案了
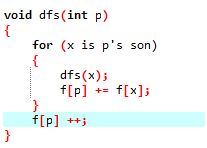
因为还没有学图论的缘故吧，不大好实现，就写伪代码来理解意思好了
看个正常点的例子
给你一个n个点的树，求它的直径
直径：在这棵树上找到两个点，使他们的距离最远
树上的任何一条路径都是先向上再向下，长这样
但是为了纯粹计算长度而不考虑方向，我们试着换换方向，
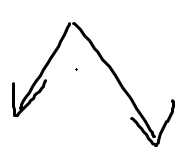
一个点向下走两条路，那么经过这个点的最长路径就是其向下能达到的最长和次长的路径之和，这样我们就可以递归着来求
用F[i][0]表示i向下的最长路，F[i][1]表示i向下的次长路
最长路很好表示，就是所有儿子向下走的最大值+1
f[p][0]=max(f[p1][0],f[p2][0],...f[pk][0])+1
那么如何表示次长路？
比如说我们找到的最大的是p1，那么我们再找次长路的时候就直接算
f[p][1]=max(f[p1][0] f[p2][0],...f[pk][0])+1
但是这个是错的。。。。。。。
为什么？
因为假设F[p1][1]又是最大的，我们再找最大路的时候找到了p1，之后我们找次长路，假如p1的次长路又是剩下所有路径当中最长的，我们就会再把p1选进去，这就意味着我们在P1这条路上走了两边，这就很恶心了，所以我们直接在选完最大的之后把P1删掉就行。
一直这么算下去，直到我们算到根节点的时候就能求出来最终答案了。
区间DP
合并石子
有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动相邻的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。
F[l][r]表示把第l堆石子到第r堆石子合并为一对石子的代价
我们会发现做任何DP题的时候的都是走老三步（找状态，找边界条件，找状态转移方程）
这个题的边界条件就是L=R的时候，所以F[l][r]=0（l=r），
那么我们再来看状态转移方程，我们最后一次合并一定是把两堆石头合并成一堆石头，是把左边某一堆和右边某一堆，由于题目的限制，我们可以发现不管怎样合并，石头的顺序是不变的。
所以我们一定是可以找到一条分界线，使得左边是A1~Ap的结果，右边是Ap+1~Ar，那么我们只需要枚举一下p的位置就可以了。所以状态转移方程就是(所有的)min(f[l][p]+F[p+1][r]+sum[l][r]);
看代码
int z[manx],f[maxn][maxn]; int main() { cin>>n; for(int a=1;a<=n;a++) cin>>z[a];//表示石子数 memset(f,0x3f,sizeof(f));//初始化为无穷大 for(int a=1;a<=n;a++) f[a][a]=0; //枚举左端点，右端点，断点 for(int l=1;i<=n;l++)//枚举左端点 { for(int r=l+1;r<=n;i++)//枚举右端点 { for(int p=l;p<r;p++) { f[l][r]=min(f[l][r],f[l][p]+f[p+1][r]+sum[l][p]); //左边合并的代价+右边合并的代价+这段区间的石子之和 } } } cout<<f[1][n]<<endl; return 0； }
先把所有的数组赋值，然后改一下边界条件
我们枚举一个左端点，枚举一个右端点，再枚举一个断点
很不幸，这种枚举方式是错的
因为在任何时候，他都不满足DP的阶段性
你看啊，你在算f[1][n]时要用到f[2][n]，但它还没有被算过（什么鬼东西）
所以我们就得枚举区间长度，然后修改一下代码就可以了
int z[manx],f[maxn][maxn]; int main() { cin>>n; for(int a=1;a<=n;a++) cin>>z[a];//表示石子数 memset(f,0x3f,sizeof(f));//初始化为无穷大 for(int a=1;a<=n;a++) f[a][a]=0; for(int len=2;len<=n;len++)//枚举区间长度 { for(int l=1,r=len;r<=n;l++,r++)//枚举区间位置 { for(int p=l;p<r;p++) { f[l][r]=min(f[l][r],f[l][p]+f[p+1][r]+sum[l][p]); //左边合并的代价+右边合并的代价+这段区间的石子之和 （用前缀和计算，在输入的时候就进行储存） } } } cout<<f[1][n]<<endl; return 0； }
因为有三重循环，所以复杂度是O(n^3)（我都没想到会这么慢）
但是题目中说到A1和An是相邻的，怎么办？
这个时候我们在后面加一个A1，然后算min（F[1][n],F[2][n+1]），但是我们又会发现，我们算后者的时候，又会出现A2和A1不相邻的情况，我们就又得加A2，然后就一直一直加，最后我们相当于对于两个一样的序列进行DP，最后搞成这样
a1,a2,....,an,a1,a2,....,an
最终的答案就是min(f[1][n],f[2][n+1],f[3][n+2],f[4][n+3]....)
那么这样理解为什么正确呢？
我们把两个点合并，相当于去掉了一条边
只需要合并n-1次，这样的话至少有一条边没有用到，可以看成把这条边断开，就变成了断开的答案
所以我们刚才就是在枚举到底断开哪一条边
仍然是一遍dp，只不过区间变成了两边
状压DP
总共给你n个坐标系上的点（x1，y1）.......（xn，yn）
这个和最小生成树没啥关系，就是个非常简单的二维平面图，你可以随便走（大雾
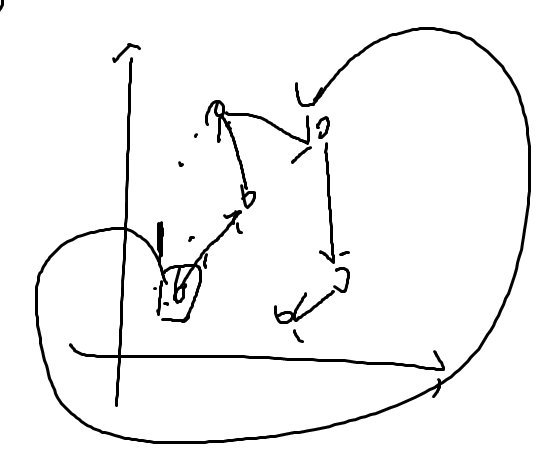
叫做TSP问题，也叫旅行商问题·，这其实是一个NP-hard问题（1171）
就是说不管写得有多快，它的时间复杂度最快也是2^n，至于证明嘛，，，，，，等学到钟神那个级别再说吧
首先每一个点最多只需要走一次（最优情况下），其次是两点之间肯定是线段最短、
我们要记录的是走过的点和没有走过的点
此时我们要考虑从5到3,4,6这三个点的所有情况，也就是说我们可以转移的所有状态分别是
1,2,5,3到4,6
1,2,5,6到3,4
1,2,5,4到3,6
我们希望把集合表示成数组的下标，就可以用二进制，对于每一个元素，我们用二进制表示在不在这个集合当中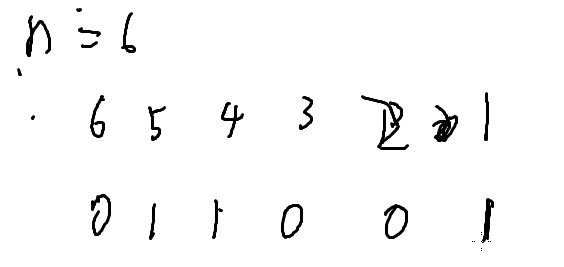
如果第i各元素，那么令第i位二进制数为1，否则为0
上面那个二进制数011001就是和（1,4,5）是等价的，这就是状态压缩的思想，用数去代表状态，真是很巧妙啊
F[s][i]s表示我们已经走过的数的集合（十进制表示），i表示最后停留在i点，总共表示从起始点走到i点的最小距离是多少；
看一看边界条件，F[1][1]=0；我们走了第一个点，而且当前在第一号点。
因为每一个点都要走一次，所以我们要对于j进行一个特判，然后状态转移成F[ s∪ { j } ] [ j ]（就是把j并到之前走过的点的集合s当中）
我们假设二进制的第0位是1，也就是第1个元素，要注意，初始化的时候是不能用memset的，因为两个点之间的距离是一个实数，memset只支持正数赋值，所以我们跑一个循环
F[1][0]=0是指我们从0号点开始，现在在0号点，所以最短距离是0（起始点就是0号点）
我们到底怎么循环呢？
其实我们走完一条路的时候，就是不断的把0变成1的过程，也就是总是有一个较小的s变成较大的。，因此我们枚举一个s从1到2^n-1，而且要枚举i这个点，可是我们在枚举的时候，不能保证i一定在当前走过的集合当中，所以我们就得加一个特判
我们把s的二进制右移i位，那么i的位置就是在个位数上，加上一个&运算
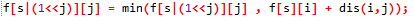
这里F[s|(1<<j)][j]就是表示 `
如果说二进制的第i位是1的话，说明i被走过，在集合当中。
随后得到转移方程我们要取（原本的状态加上第i个点到第j个点的距离）
所以最后算答案的话，就应该枚举一下所有元素都在集合例，最后停留的点1~n，取一个min之后输出
来看一看代码
int n,f[233]; double f[2^n][n]; //因为点集是用二进制数表示的，如果都在的话最多就是2^n //每一个点在或者不在，所以是n double dis(int i,int j) { return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//距离公式 } int main() { cin>>n; for(int a=0;a<n;a++) { cin>>x[a]>>y[a]; //注意这里是从0开始，因为二进制最低位是从2^0开始的 } for(int a=0;a<(1<<n);a++) { for(int b=0;b<n;b++) { f[a][b]=1e+20;//因为要最小值，所以赋值为无穷大 } } f[1][0]=0//因为下标都减了一 ，所以从零号点开始 //二进制数为 0 0 0 0....0 0 1转化到十进制就是1 //应该先枚举s还是i？ //我们走的时候到达的点不断变多，也就是二进制的0不断变成1 //也就是s不断变大，所以把s从小到大来枚举 for(int s=1;i<(1<<n);s++)//枚举已经走过的点 { for(int i=0;i<n;i++)//枚举停留的点 { //但是如果这样的话有可能i不在集合s中，所以我们要判断 if(((s>>i)&1)==1)//右移i位的话他的第i位就移到了最低位 //如果第i位=1的话，就说明i在这个集合里面 { //转移：从剩下没有走过的点里枚举 for(int j=0;j<n;j++) { if(((s>>j)&1)==0)//如果不在这个集合中，就说明可以走 { f[s|(1<<j)][j]=min(f[s|(1<<j)][j],f[s][i]+dis(i,j));//s|(1<<j):把s的二进制第j位变成1 } } } } } double ans=1e+20; for(int a=1;a<n;a++) ans=min(ans,f[(1<<j)-1][a]);//枚举终点 cout<<ans<<endl; }
状态压缩和动态规划加起来的话，它的时间复杂度是O(n^2*2^n)的
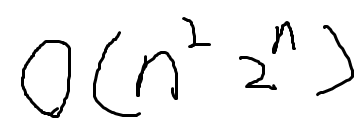
一般来说，状压DP的n<=20，所以我们看到类似的数据范围，就要想到用状压DP
这里一块说一说数据范围的一些事情吧
计算机一秒的运算量差不多在3*10^8~10^9之间（当然我严重怀疑NOIP测评姬会更慢）
所以说还是得注意着n的大小一点
n<=12（O(n!)的复杂度，直接暴搜）
n<=22 （状压）
n<=32 (直接放弃)（我也没听明白钟神讲的是个啥，反正很变态）
n<=50 (直接放弃)
n<=100 (O(n^3))
n<=1000 (O(n^2))
n<=10^5 (数据结构)
n<=10^6 (线性算法)（其实我感觉1e6是非常常见的数据范围，一般情况下只要不是算法太烂基本上都能过）
其他DP
只需要记住题目每多一个条件就多一个维度，其他DP这东西和搜索的剪枝差不多，不一定一定做对，但是肯定有点用，只要我们的状态转移方程是没有问题的，那基本上是能拿到暴力分
一道例题
N*M的方格图
只能向右或者向下
走到右下的方案数？
走到右下的最小代价？
F[i][j]表示在第i行第j列的方案数，首先F[1][j]=1和F[i][1]=1，因为直着走一定是只有一种方法走到那个点的
所以转移方程就是
P1216 [IOI1994][USACO1.5]数字三角形 Number Triangles
用DP来解
因为我们是从顶点开始走，往左下走或者右下走，所以我们的状态就是F[i][j]我们停在第i行第j列所能达到的最大权值
对于每一个点，我们看他是从哪一个点过来的，可以是右上面也可以是左上面
转移方程：f[i][j]=max(f[i-1][j-1]+f[i-1][j])+a[i][j]
QWQ终于是有一个能码出来的代码了
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int r,a[1001][1001],qaq[1001][1001],MAX; int main() { cin>>r; for(int i=1; i<=r; ++i)//第i行第j个 for(int j=1; j<=i; ++j) cin>>a[i][j]; for(int i=1; i<=r; ++i) for(int j=1; j<=i; ++j) { qaq[i][j]=max(qaq[i-1][j-1],qaq[i-1][j])+a[i][j]; } for(int i=1; i<=r; ++i) MAX=max(MAX,qaq[r][i]); cout<<MAX; return 0; }
改造题目（EX NumberTriangles）
我们要使得找出来的权值和%m之后的值是最大的，
起初我的想法是用一个结构体来存实际权值和取模后的权值，但是是不行的，因为不再满足最优子结构原则了。（就是说实际权值和取模权值之间的大小没有必然联系，所以我们无法用状态转移方程来求最大最小）
我们考虑加一个维度，开一个bool数组f
f[i][j][k]代表走到第i行第j列是路径权值和%m= k 可不可能，那我们怎么转移呢
还是考虑一个点只有可能从它的左上方和右上方求值过来，那么我们就能得出状态转移方程了
for (int i = 1; i <= n; ++i) { for (int j = 1; j <= m; ++j) { if (f[n][i][j]) ans = max(ans, j); } }
最长上升子序列
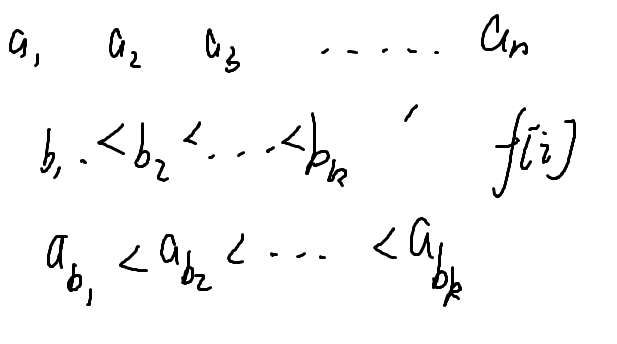
转移的话就是枚举i前面的aj小于Ai的数
for (int i = 1; i <= n; ++i) for (int j = 1; j <= i; ++j) f[i] = max(f[i], f[j] + i);
不是很难啊，时间复杂度是N^2
但是我们把数据加强到n<=1e5了，那么怎么办呢
我们肯定不能再跑一次O(n^2)了啊，这里就考虑用线段树
就是运用一次昨天学习的线段树求区间最值的方法，把时间复杂度直接降到logn，这样一来，总的时间复杂度就是nlogn
v=max(a1,a2,a3,.....an)，每次计算f[i]
我们建一颗长度为n的线段树，然后直接进行划分，就是说两端区间的最长上升子序列就肯定是他的两个儿子的和，这样算起来就快不少了
背包问题（看看背包九讲）
01背包
最基本的背包问题是说你有n个物品，第i个物品的价值是vi，体积是mi，求不超过背包容积的最大价值
对于第i个物品，要么放进背包，要么不放进背包
F[i][j]表示前i个物品已经用了j的体积，能够带来的最大价值；
状态转移就是第i+1个物品放不放进背包
不放的话就是F[i+1][j]
放的话就是F[i+1][j+v[i+1]]
所以状态转移方程就是qaq[j]=max(qaq[j-t[i]]+v[i],qaq[j]);
完全背包
我们所有的物品都是无数个的，还是求不超过背包容积的最大价值
这里我们状态仍然是不变的，接下来考虑这个物品到底要用多少个
我们枚举x表示第i+1个物品要放进去几个，这么暴力枚举倒是也能过，但是很慢，时间复杂度大约是O(n*m^2)的
我们把方程换成
求在[l,r]中满足各位数字之积为k的数有多少个
一看就知道是数位DP
直观想法还是转移到0~r和0~l-1F[i][j][k]表示从高到低填到第i位，j=1表示小于，j=0表示等于，K表示所有的数位的乘积
但是我们会发现，k最大可以达到9^18，肯定是存不下的，所以我们得换个方法
首先我们会发现，各位数字，一定是不超过9的，而9以内的指数只有2 3 5 7
所以k一定可以写成2^a*3^b*5^c*7^d的形式，所以我们把状态F[i][j][a][b][c][d]改为i表示填到i位，j=0，v<x，j=1，v=x
很神奇的是我们暴力枚举四个循环，竟然时间复杂度是不会爆掉的，这也让我不禁考虑我平时是不是对于时间复杂度过于重视了