一、引入
变分自编码器属于一种深度生成模型,这是从最终结果来看的,因为这个模型最后生成了一些符合模型分布的新样本。深度生成模型就是利用神经网络强大的拟合能力,来建模一个分布或者干脆直接生成一些新的符合这个复杂分布的样本。
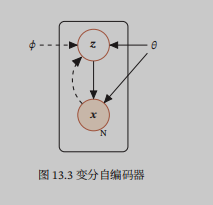
用盘子表示法如上,其中虚线部分表示变分近似,实线表示生成模型。从这个图大体可以描述一下变分自编码器中的随机变量在干什么:
首先针对于这个模型中的所有随机变量(包括可观测变量x和隐变量z),有一个联合概率分布$p(x,z; heta )$,其中隐变量z是相对较为低维空间中的随机变量,而可观测变量x相对高维,这也符合我们的认知,我们观察到的很多现象都是由很多小事共同作用而成的,比如一位同学考了200分,我们能观察到这个结果,但是我们不能知道这200分的背后具体哪些科目优秀哪些科目考差了,200分相对于具体科目而言,是个比较复杂的高维的事件。
其次,因为我们只能看见$x$,而且我们说的生成样本也只是生成$x$,不关心背后的隐变量,所以我们需要更进一步的知道$p(x; heta )$,这个也叫边际分布,需要对联合概率分布$p(x,z; heta )$中的$z$进行求和而得到:
$p(x; heta )=sum_{z}^{ }p(x,z; heta )$
上式求和比较困难,毕竟我们看不见隐变量,更无从知道它的取值和概率。于是,我们采用条件概率公式分解,然后再看能不能用对数似然的方法求解,所以我们直接考虑$logp(x; heta )$:
$logp(x; heta )=logfrac{p(x,z; heta )}{p(zmid x; heta )}$
对于这个式子,进一步进行拆分如下:
$logp(x; heta )=logfrac{p(x,z; heta )}{p(zmid x; heta )}
=logp(x,z; heta )-logp(zmid x; heta )
=logfrac{p(x,z; heta )}{q(z;phi )}-logfrac{p(zmid x; heta )}{q(z;phi )}
=int q(z;phi )logfrac{p(x,z; heta )}{q(z;phi )}dz-int q(z;phi )logfrac{p(zmid x; heta )}{q(z;phi )}dz
=ELBO+KL(q(z;phi )parallel p(zmid x; heta ))$
我们现在知道了$logp(x; heta )$可以由$ELBO$和$KL$散度来衡量,$KL$散度始终大于0,如果$KL$散度为0,那么我们优化这个对数似然$logp(x; heta )$就可以变成优化$ELBO$这个证据下界了。我们知道,当$q(z;phi )=p(zmid x; heta )$时,$KL$散度为0,最后问题就会变成寻找一个$ heta$使得$ELBO$最大即可。这个优化过程也可以用EM算法来描述:
E步:固定$ heta$,寻找一个$phi$,使得$q(z;phi )$接近$p(zmid x; heta )$,当然这个$p(zmid x; heta )$的求解通常是一个变分推断的问题,也就是用简单的$q(z;phi )$来近似;
M步:固定上一步找到的$phi$,也就是固定$q(z;phi )$,来寻找一个当下最好的$ heta$,在上一步中,因为找到的$q(z;phi )$接近$p(zmid x; heta )$,我们就当$KL$散度为0了,所以只用考虑此时的$ELBO$。
E步:现在$ heta$已经更新了,此时的$ heta$和我们第一次E步中找到的$q(z;phi )$,使得我们的$KL$散度不再为0,也就是说此时的$q(z;phi )$不是最优的了,我们固定好这个更新后的$ heta$,重新去寻找新的$q(z;phi )$来拟合目前的$p(zmid x; heta )$
M步:现在$q(z;phi )$也更新了,$KL$散度重新变成了0,又可以愉快的固定$q(z;phi )$去寻找新的最优的$ heta$了。
上述步骤不断重复,直到稳定。
但是这个过程还有些比较复杂的问题有待解决:
怎么样使得$q(z;phi )$接近$p(zmid x; heta )$?答案是近似推断的方法,比如变分推断,采样法之类的,但是如果$p(zmid x; heta )$很复杂,这些手法都不大好。
在优化$EBLO$时,也涉及一个联合概率分布,自然此时我们就要通过条件概率公式对其进行拆解:$p(x,z; heta )=p(xmid z; heta )p(z; heta )$,对于$p(xmid z; heta )$如何近似也是个问题。
二、变分自编码器
变分自编码器有推断网络和生成网络组成。
(一)推断网络
用神经网络来近似$q(z;phi )$,因为$q(z;phi )$的目标是近似$p(zmid x; heta )$,所以即便使用神经网络得到的$q(z;phi )$理论上并不依赖$x$,任然习惯性写作$q(zmid x;phi )$。推断网络的输入为x,输出为分布$q(zmid x;phi )$,为了简单,通常假设$q(zmid x;phi )$是参数化的高斯分布,所以输出其实是高斯分布的均值和方差。
(二)生成网络
生成模型分为两部分,$p(xmid z; heta )$和先验$p(z; heta )$,先验是标准正太分布。
其中我们可以用生成网络来近似$p(xmid z; heta )$,输入为$z$,输出为分布$p(xmid z; heta )$。
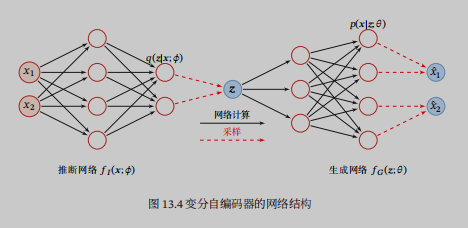
在自编码器中,编码器和解码器的输出都是编码,而在变分自编码器中,输出的是分布或分布的参数。二者只是在网络结构上相似。
注意,之所以采用神经网络来拟合,是因为我们没办法直接计算或者是用变分推断来近似隐变量z的后验,所以这里我们的推断网络的目标函数,是最大化EBLO,而不是最小化KL,之前我们得到需要$q(z;phi )=p(zmid x; heta )$这个结论,是因为之前的背景是要么可以精确计算要么可以近似推断,现在没办法计算和近似$p(zmid x; heta )$了,所以我们说推断网络的目标是最大化EBLO,否则在最小化KL散度中将有两个变量$q(z;phi )$和$p(zmid x; heta )$。认定推断网络的目标是最大化EBLO还有一个好处就是同生成网络的目标是一样的了。
所以这连续几篇文章的主要思路就是:
如果z的后验p(zmid x; heta )$可以精确计算,我们就计算出来,然后套用EM算法;
如果不可以精确计算,那么就近似吧,顺便引入平均场的思想,也就是隐变量之间独立,然后隐变量之间进行一个迭代优化,再套用EM算法;
如果z的后验很复杂,没办法精确计算,近似推断也不不准确,那就考虑一下神经网络吧,毕竟听说神经网络理论上可以拟合任何函数,最后其实依然可以套用EM算法的思想。
然后回到变分自编码器的目标函数上来,现在知道推断网络和生成网络的目标都是最大化EBLO了,然后拆解一下EBLO,把我们在网络中生成的分布给写进去便于理解:
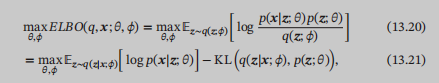
13.21的第二项,当我们知道了$q(zmid x;phi )$和$p(z; heta )$的准确值后,我们可以精确的计算出来,问题就在于第一项,初看它是一个期望,似乎可以通过蒙特卡洛采样来完成,而且在前面的图中也确实是这么做的样子。注意这里的采样是怎么采的?是针对每一个样本x,都采集M个z,来近似得到专属于这个x的一个期望!也就是说,我们有多少个样本就得这么做多少次:

而不是说,当我通过神经网络得到了一个z的后验分布$q(zmid x;phi )$,我就可以采a个z,然后得到a个新x,和旧x进行比较,这样是没有道理的。我们不知道得到的新的一组新x和旧x谁和谁才是对应的关系。所以我们要针对每一个样本x,做M次隐变量z的采样,来近似得到结果。
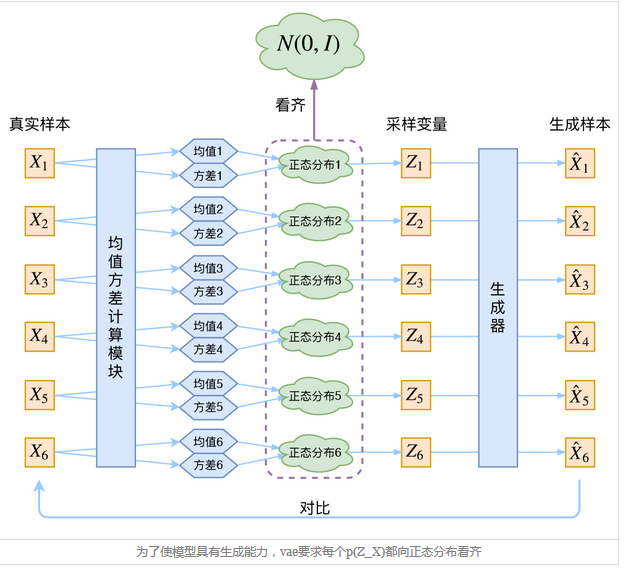
来源:https://spaces.ac.cn/archives/5253
这个图告诉我们一件事情,原来推断网络,最开始是每个样本都通过神经网络进行了均值方差的计算,得到了多个后验概率分布,然后让它们统统近似标准正态分布,再从中进行采样。也就是说,每个样本通过推断网络,都会有一个专属它的后验概率分布,只是这些概率分布都近似N(0,1)而已,这样肯定能保证我们最后生成的x和原样本x是一一对应的。
之前看的时候,一直很不能理解的一个问题是:在推断网络中,我得到了一个$q(zmid x;phi )$,然后再从里面采样z?然后生成网络再生成一个$q(xmid z;phi )$?感觉一直怪怪的,没法联系起来,按道理来说,我应该是从z的先验中采样,再从$q(xmid z;phi )$采样才对啊,可是很多地方都没有提到过z的先验分布的存在,书里也只是在讲生成网络的时候,草草的说明z的先验是标准正太分布。原来真正的原因是:
如果我们可以像上图一样,针对每一个样本都训练出属于它的正太分布,并且要求所有样本的正态分布都近似标准正太分布,那么所有正态分布的总的效应就相当于z的先验是正态分布:
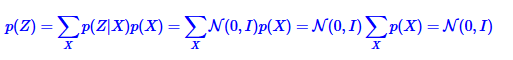
原来只要保证了所有样本的分布都近似标准正太,则可以得到z的先验也是标准正态分布;要求所有样本的分布都近似标准正太还有个原因,生成网络希望得到的结果与原样本相近,如果没有这个要求,最后模型会渐渐失去不确定性,方差会逐渐变为0。
其实直接采样并不是一个好的选择。