被迫营业
目前进度: (10/11)
A.【POJ2201】Cartesian Tree 手推车树
原题链接
板子,一定有解,单调栈维护右链即可。
为了使 ( exttt{Key}) 有序,需要排序,(O(n log n))。
代码
const int N=50050;
int n,stk[N],qwq[N],tp,fa[N],ch[N][2];
struct node{int k,val,id;}a[N];
inline bool cmp(node a,node b){return a.k<b.k;}
inline void build()
{
fr(i,1,n)
{
int k=tp;
while(k&&a[stk[k]].val>a[i].val) --k;
if(k) ch[stk[k]][1]=i;
if(k<tp) ch[i][0]=stk[k+1];
stk[++k]=i,tp=k;
}
return ;
}
int main(void)
{
n=read();
fr(i,1,n)
{
int k=read(),val=read();
a[i]=(node){k,val,i};
}
sort(a+1,a+n+1,cmp),build(),puts("YES");
fr(i,1,n) qwq[a[i].id]=i;
fr(i,1,n) fa[ch[i][0]]=fa[ch[i][1]]=i;
fr(i,1,n) printf("%d %d %d
",a[fa[qwq[i]]].id,a[ch[qwq[i]][0]].id,a[ch[qwq[i]][1]].id);
return 0;
}
B.【POJ1470】Closest Common Ancestors
原题链接
为啥又是板子
倍增 LCA 即可,注意多测。
代码
const int N=1050;
int n,q,f[N][15],head[N],tot[N],dep[N],root,in[N],cnt;
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int fa)
{
f[u][0]=fa,dep[u]=dep[fa]+1;
fr(i,1,14) f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
dfs(v,u);
}
return ;
}
inline int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
pfr(i,14,0) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
pfr(i,14,0) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
int main(void)
{
while(~scanf("%d",&n))
{
root=cnt=0;
memset(f,0,sizeof(f));
memset(dep,0,sizeof(int)*(n+1));
memset(in,0,sizeof(int)*(n+1));
memset(tot,0,sizeof(int)*(n+1));
memset(head,0,sizeof(int)*(n+1));
fr(i,1,n)
{
int u=read(),tmp=read();
while(tmp--)
{
int v=read();
add(u,v),add(v,u),++in[v];
}
}
fr(i,1,n) if(!in[i]) root=i;
dfs(root,0);
q=read();
while(q--) ++tot[lca(read(),read())];
fr(i,1,n) if(tot[i]) printf("%d:%d
",i,tot[i]);
}
return 0;
}
C.【HDU1506】Largest Rectangle in a Histogram
原题链接
为啥又双叒叕是板子啊
经典题,单调栈维护即可,注意开long long。
代码
const ll N=1e5+50;
ll n,a[N],l[N],r[N],ans,top;
struct node{ll id,val;}st[N];
int main(void)
{
while(n=read())
{
ans=top=0;
memset(l,0,sizeof(ll)*(n+1));
memset(r,0,sizeof(ll)*(n+1));
fr(i,1,n) a[i]=read();
st[++top]=(node){1,a[1]};
fr(i,2,n)
{
while(a[i]<st[top].val) r[st[top].id]=i-1,--top;
st[++top]=(node){i,a[i]};
}
while(top) r[st[top].id]=n,--top;
st[++top]=(node){n,a[n]};
pfr(i,n-1,1)
{
while(a[i]<st[top].val) l[st[top].id]=i+1,--top;
st[++top]=(node){i,a[i]};
}
while(top) l[st[top].id]=1,--top;
fr(i,1,n) ans=max(ans,a[i]*(r[i]-l[i]+1));
writeln(ans);
}
return 0;
}
D.【HDU6228】Tree 大尺寸埃克
原题链接
思维题。
首先如果删去一条边后剩下的两个子树中含有同一种颜色,那么这条边显然会被这种颜色覆盖。
被恰好覆盖 (k) 次的边将会被计入答案。
大力猜结论:如果两个子树大小都 (geq k),那么 ++ans,否则则不可能被覆盖。
必要性显然,对于充分性,给出一个非常猎奇的证明:
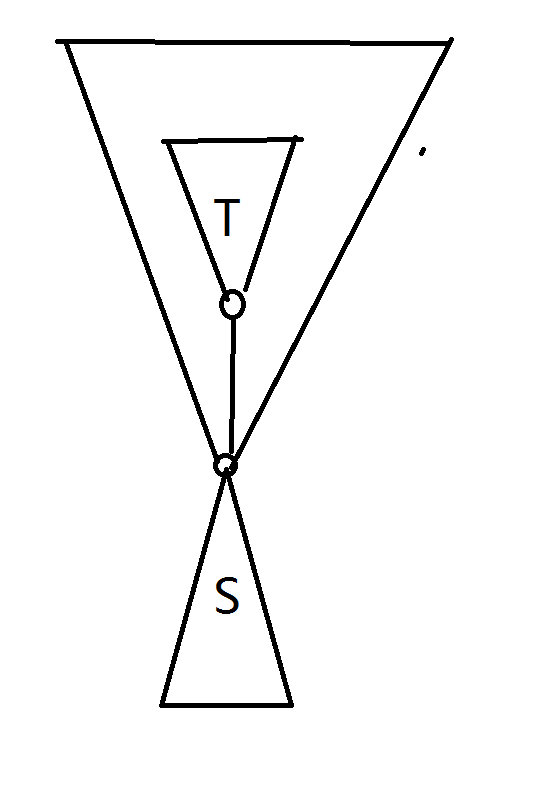
找出这棵树中最小的 (geq k) 的子树,将这个子树内的点染出 (k) 种颜色(一定可以做到),然后从这个点开始 dfs。
dfs 到最后,直到接下来需要遍历的子树大小 (< k) 时停止(比如 dfs 到 (T) ),包含一开始的子树的子树大小一直变大,不会出现矛盾,那么将 (T) 内的点染出 (k) 种颜色,则从一开始的点到当前点的链上的所有点都可以被覆盖 (k) 次,都能被计入答案。
由于是 (dfs),所有可能被计入答案的点都被统计到了,没有遍历的点一定不可能计入答案,所以是对的。
代码
const int N=2e5+50;
int n,k,head[N],cnt,sz[N],ans;
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int fa)
{
sz[u]=1;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
dfs(v,u),sz[u]+=sz[v],ans+=(n-sz[v]>=k&&sz[v]>=k);
}
return ;
}
int main(void)
{
int T=read();
while(T--)
{
n=read(),k=read(),cnt=ans=0;
memset(head,0,sizeof(int)*(n+1));
memset(sz,0,sizeof(int)*(n+1));
fr(i,1,n-1)
{
int u=read(),v=read();
add(u,v),add(v,u);
}
dfs(1,0);
writeln(ans);
}
return 0;
}
E.【HDU6241】Color a Tree
原题链接
观察到限制+最值,可以考虑二分。
子树外的限制很难处理,考虑如何转化为子树内的。
如果一共选了 (k) 个点,则 (b_i) 等价于 (i) 的子树内至多选 (k-b_i) 个点,这样相当于给每个点设了一个上下界,二分这个 (k)。
在 (dfs) 过程中累加儿子的上下界更新当前点的上下界,最后需要满足每个点的上下界不矛盾。
注意最后需要满足 (l_root leq x leq r_root),(x) 是当前二分的值。
代码
const int N=2e5+50;
int n,head[N],cnt,ma,mb,a[N],b[N],l[N],r[N],sz[N],ans;
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs1(int u,int fa)
{
sz[u]=1;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
dfs1(v,u);
sz[u]+=sz[v];
}
return ;
}
bool dfs(int u,int fa)
{
int L=0,R=1;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
if(!dfs(v,u)) return false;
L+=l[v],R+=r[v];
}
l[u]=max(l[u],L),r[u]=min(r[u],R);
return l[u]<=r[u];
}
inline bool check(int x)
{
fr(i,1,n) l[i]=a[i],r[i]=min(sz[i],x-b[i]);
return dfs(1,0)&&l[1]<=x&&x<=r[1];
}
int main(void)
{
int T=read();
while(T--)
{
n=read(),cnt=0,ans=-1;
memset(sz,0,sizeof(int)*(n+1));
memset(head,0,sizeof(int)*(n+1));
memset(a,0,sizeof(int)*(n+1));
memset(b,0,sizeof(int)*(n+1));
fr(i,1,n-1)
{
int u=read(),v=read();
add(u,v),add(v,u);
}
dfs1(1,0);
ma=read();
fr(i,1,ma)
{
int x=read(),y=read();
a[x]=max(a[x],y);
}
mb=read();
fr(i,1,mb)
{
int x=read(),y=read();
b[x]=max(b[x],y);
}
int l=0,r=n;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)){ans=mid,r=mid-1;}
else l=mid+1;
}
writeln(ans);
}
return 0;
}
F.【HDU 5469】Antonidas
原题链接
不会点分治,咕了。
G.【CF1304E】1-Trees and Queries
原题链接
首先倍增 LCA,方便后面查询树上距离。
注意到每次只加一条边,不妨对此分类讨论:
- 当 ((a,b)) 不经过 ((x,y)) 时,所得的简单路径长度为 (dis(a,b))
- 当 ((a,b)) 经过 ((x,y)) 时,所得的简单路径长度为 (dis(a,x)+1+dis(y,b)) 或 (dis(a,y)+1+dis(x,b))
以上三者之一中只要有一条路径 (d) 满足长度 (leq k) 且 路径长度与(k) 模 (2) 同余即可。
代码
const int N=1e5+50;
int n,q,f[N][21],head[N],dep[N],cnt;
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1;
for(int i=1;(1<<i)<=dep[u];i++) f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
f[v][0]=u;
dfs(v,u);
}
}
inline int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
#define dis(x,y) dep[x]+dep[y]-(dep[lca(x,y)]<<1)
int main(void)
{
n=read();
fr(i,1,n-1)
{
int u=read(),v=read();
add(u,v),add(v,u);
}
dfs(1,0);
q=read();
while(q--)
{
int x=read(),y=read(),a=read(),b=read(),k=read();
int d1=dis(a,b),d2=dis(a,x)+1+dis(y,b),d3=dis(a,y)+1+dis(b,x);
if(d1>k&&d2>k&&d3>k){puts("NO");continue;}
if(d1<=k&&!((k-d1)&1)){puts("YES");continue;}
if(d2<=k&&!((k-d2)&1)){puts("YES");continue;}
if(d3<=k&&!((k-d3)&1)){puts("YES");continue;}
puts("NO");
}
return 0;
}
H.【HDU 4777】Rabbit Kingdom
原题链接
先预处理出每个数 (a_i) 左边和右边离它最近的和他不互质的数的位置 (l_i,r_i),那么对于一个询问 ((L,R)),一个 (i) 对其有贡献等价于 (l_i < L leq i leq R < r_i)。
离线后树状数组维护即可,注意 vector 的清空。
需要特判掉左边不存在不与其互质的数以及右边不存在不与其互质的数的情况,细节稍多。
代码
const int N=2e5+50;
int n,m,a[N],t[N],l[N],r[N],vis[N],ans[N],lst[N];
struct node{int id,r;};
struct que{int l,r,id;}q[N];
vector<int> fac[N];
vector<node> vec[N];
inline bool cmp(que a,que b){return (a.l==b.l)?a.r<b.r:a.l<b.l;}
#define lowbit(x) x&(-x)
inline void add(int x,int dlt)
{
while(x<=n) t[x]+=dlt,x+=lowbit(x);
return ;
}
inline int query(int x)
{
int ans=0;
while(x) ans+=t[x],x-=lowbit(x);
return ans;
}
inline void init(int n)
{
fr(i,2,n) if(!vis[i]) for(int j=i;j<=n;j+=i) vis[j]=1,fac[j].push_back(i);
return ;
}
int main(void)
{
init(N-49);
while(n=read())
{
fr(i,1,n) vec[i].clear();
m=read();
memset(t,0,sizeof(t));
fr(i,1,n) a[i]=read();
fr(i,1,m) q[i].l=read(),q[i].r=read(),q[i].id=i;
sort(q+1,q+m+1,cmp);
memset(l,0,sizeof(int)*(n+1)),memset(lst,0,sizeof(lst));
fr(i,1,n) r[i]=n+1;
fr(i,1,n)
{
int sz=fac[a[i]].size();
fr(j,0,sz-1)
{
int cur=fac[a[i]][j];
if(lst[cur])
{
l[i]=max(l[i],lst[cur]),r[lst[cur]]=min(r[lst[cur]],i);
// printf("update r of %d: r[%d]=min(r[%d],%d)",lst[cur],lst[cur],)
}
lst[cur]=i;
}
}
fr(i,1,n)
{
if(l[i]<1)
{
add(i,1);
if(r[i]<=n) add(r[i],-1);
}
else
{
vec[l[i]].push_back((node){i,r[i]});
// printf("vec[%d].push_back((node){%d,%d})
",l[i],i,r[i]);
}
}
int cur=1;
fr(i,1,m)
{
while(cur<q[i].l)
{
add(cur,-1);
if(r[cur]<=n) add(r[cur],1);
int sz=vec[cur].size();
fr(j,0,sz-1)
{
add(vec[cur][j].id,1);
if(vec[cur][j].r<=n) add(vec[cur][j].r,-1);
}
++cur;
}
ans[q[i].id]=query(q[i].r)-query(q[i].l-1);
}
fr(i,1,m) writeln(ans[i]);
}
return 0;
}
I.【HDU4902】 Nice boat
题目背景好评
ODT 可以直接莽过去,这里就不提了。
考虑如果没有操作 1 怎么做。
每个数与其他数取 (gcd) 之后至少会 (/2) ,于是每次直接暴力处理即可(类似于花神),复杂度 (O(n log^2 n))。
然后如果有区间覆盖操作显然会被卡爆,考虑在一个区间被完全覆盖之后打上一个标记,每次遇到一个标记直接与整个区间的值取 (gcd),然后把得到的值做区间覆盖,这样子就可以了。
总复杂度 (O(n log^2 n))。
注意区间覆盖有可能覆盖为 (0),所以 (tag) 的值一开始要设成 (-1)。
代码
const ll N=1e5+50;
ll n,q,a[N];
inline ll gcd(ll a,ll b){return (b==0)?a:gcd(b,a%b);}
#define ls x<<1
#define rs x<<1|1
struct segment{ll vis,maxn,tag;}t[N<<2];
inline void pushup(int x)
{
t[x].maxn=max(t[ls].maxn,t[rs].maxn);
if(t[ls].maxn==t[rs].maxn&&t[ls].vis&&t[rs].vis) t[x].vis=1;
else t[x].vis=0;
}
inline void pushdown(ll x)
{
if(t[x].tag==-1) return ;
t[ls].tag=t[rs].tag=t[x].tag,t[ls].maxn=t[rs].maxn=t[x].tag,t[ls].vis=t[rs].vis=1,t[x].tag=-1;
return ;
}
void build(ll x,ll l,ll r)
{
if(l==r){t[x].maxn=a[l],t[x].tag=-1;return ;}
ll mid=(l+r)>>1;
build(ls,l,mid),build(rs,mid+1,r);
t[x].tag=-1,pushup(x);
return ;
}
void modify1(ll x,ll l,ll r,ll ql,ll qr,ll val)
{
if(ql<=l&&r<=qr){t[x].maxn=t[x].tag=val,t[x].vis=1;return ;}
pushdown(x);
ll mid=(l+r)>>1;
if(ql<=mid) modify1(ls,l,mid,ql,qr,val);
if(qr>mid) modify1(rs,mid+1,r,ql,qr,val);
pushup(x);
return ;
}
void modify2(ll x,ll l,ll r,ll ql,ll qr,ll val)
{
if(t[x].maxn<=val) return ;
if(ql<=l&&r<=qr&&t[x].vis){t[x].maxn=gcd(t[x].maxn,val),t[x].tag=t[x].maxn;return;}
if(l==r){t[x].maxn=gcd(t[x].maxn,val);return ;}
pushdown(x);
ll mid=(l+r)>>1;
if(ql<=mid) modify2(ls,l,mid,ql,qr,val);
if(qr>mid) modify2(rs,mid+1,r,ql,qr,val);
pushup(x);
return ;
}
ll query(ll x,ll l,ll r,ll pos)
{
if(l==r) return t[x].maxn;
pushdown(x);
ll mid=(l+r)>>1;
if(pos<=mid) return query(ls,l,mid,pos);
else return query(rs,mid+1,r,pos);
}
int main(void)
{
ll T=read();
while(T--)
{
n=read();
fr(i,1,n) a[i]=read();
build(1,1,n);
q=read();
while(q--)
{
ll opt=read(),l=read(),r=read(),x=read();
if(opt==1) modify1(1,1,n,l,r,x);
else modify2(1,1,n,l,r,x);
}
fr(i,1,n) writesp(query(1,1,n,i));
enter;
}
return 0;
}
J.【Gym 102501G】Swapping Places
感谢 @kunyi 大佬。
观察到除了好朋友以外的先后顺序是固定的,那么可以利用此进行拓扑排序,即将不是好朋友以及是好朋友但不相邻的点之间大力连边,但是这样边数显然爆炸,考虑优化。
在遍历的过程中开个桶记录一下某个物种出现最近的位置,若那个物种与现在枚举的位置不是好朋友,将那个位置与当前位置连边,因为先后关系具有传递性,只需连最近的就可以了。
如果两个点((u,v))是好朋友且中间都是好朋友,不会连边;而如果他们中间隔了一个与他们都不是好朋友的点 (x),就会有 (u
ightarrow x),(x
ightarrow v) 这样的两条边,保证了他们的先后顺序,所以是对的。
总边数以及总复杂度都是 (O(ns))。
代码
const int N=250,M=1e5+5;
int s,l,n,a[M],g[N][N],tmp[M],head[M],in[M],ans[M],tot,cnt;
struct edge{int to,nxt;}e[M*200];
inline void add(int u,int v)
{
e[++tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
}
string name[M],qwq1,qwq2;
map<string,int> mp;
inline bool cmp(string a,string b){return a+b<b+a;}
#define fir first
#define sec second
#define MP make_pair
priority_queue<pair<int,int> > q;
int main(void)
{
ios::sync_with_stdio(false);
cin>>s>>l>>n;
fr(i,1,s) cin>>name[i];
sort(name+1,name+s+1,cmp);
fr(i,1,s) mp[name[i]]=i;
fr(i,1,l)
{
cin>>qwq1>>qwq2;
g[mp[qwq1]][mp[qwq2]]=1;
g[mp[qwq2]][mp[qwq1]]=1;
}
fr(i,1,n){cin>>qwq1;a[i]=mp[qwq1];}
fr(i,1,n)
{
fr(j,1,s) if((tmp[j]&&!g[a[i]][j]))
{
add(tmp[j],i),++in[i];
}
tmp[a[i]]=i;
}
fr(i,1,n) if(!in[i]) q.push(MP(-a[i],i));
while(!q.empty())
{
pair<int,int> f=q.top();q.pop();
ans[++cnt]=f.sec;int u=f.sec;
// printf("u: %d
",u);
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;--in[v];
// printf("u: %d v: %d
",u,v);
if(!in[v]) q.push(MP(-a[v],v));
}
}
fr(i,1,n) cout<<name[a[ans[i]]]<<" ";
return 0;
}
K.【LightOJ 1370】Bi-shoe and Phi-shoe
原题链接
发现 (1000003) 已经是一个质数了,故 (varphi(1000003) > varphi(x),x<1000003),所以只需要把 ([1,1000003]) 内的数的 (varphi) 线性筛出来即可。
然后先对于一个 (i) ,把 (varphi(x)=i) 的最小 (x) 预处理出来,做一个后缀 (min) 即可。
代码
const ll N=1e6+50,maxn=1e6+3;
ll n,phi[N],vis[N],prime[N],cnt,ans[N],minn[N],tot=0;
inline void sieve(ll n)
{
fr(i,2,n)
{
if(!vis[i]) prime[++cnt]=i,phi[i]=i-1;
for(ll j=1;j<=cnt&&i*prime[j]<=n;++j)
{
vis[i*prime[j]]=1;
if(!(i%prime[j]))
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
}
}
inline void getans(ll n)
{
memset(minn,0x3f,sizeof(minn));
pfr(i,n,1) minn[phi[i]]=min(minn[phi[i]],i);
pfr(i,n-1,1) minn[i]=min(minn[i+1],minn[i]);
return ;
}
int main(void)
{
sieve(maxn),getans(maxn);
ll T=read();
fr(t,1,T)
{
n=read(),tot=0;
fr(i,1,n) tot+=minn[read()];
printf("Case %lld: %lld Xukha
",t,tot);
}
return 0;
}