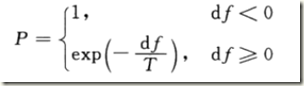1.前言
随着机器学习的发展,在求解一些问题的过程中,问题的规模逐渐加大,对这些问题的求解到很精确的解,需要花费大量的资源,还不一定能得到,当碰到这些问题时,可以通过一定的优化算法,得到问题的最优解或者近似值。例如:
旅行商问题(traveling salesman proplem TSP):给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
超大规模集成电路(Very Large Scale Integration VLSI):通常需要在几毫米见方大小的硅片上集成上万至百万晶体管、线宽在1微米以下的集成电路。由于晶体管与连线一次完成,故制作几个至上百万晶体管的工时和费用是等同的。大量生产时,硬件费用几乎可不计,而取决于设计费用。用模拟退火算法几乎可以很好地完成所有优化的VLSI设计工作。如全局布线、布板、布局和逻辑最小化等等。
图像识别与处理问题:可用来进行图像恢复等工作,即把一幅被污染的图像重新恢复成清晰的原图,滤掉其中被畸变的部分。
如此以上这些领域都是用模拟退火算法在求解,能产生令人满意的近似最优解,而且所用的时间也不很长。既然模拟退火算法有这么强大的效果,各位看官是不是迫不及待的想进入正题了,我跟你们说,先别急,在正式让模拟退火算法隆重登场之前,我们先介绍一种简单的贪心搜索算法----爬山算法。
2.爬山算法
前面我们已经说了,爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
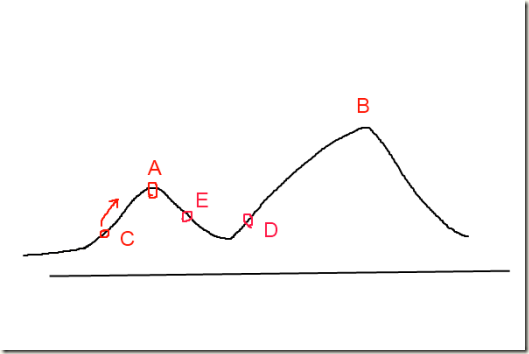
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
下面我们具体看一个爬山算法的例子
求解下面的式子
(公式-1)
下面通过Python实现在x在区间[-2,4]和y在区间[-2,4]的图像
# -*- coding: utf-8 -*- from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np fig = plt.figure() ax = Axes3D(fig) X = np.arange(-2, 4, 0.05) Y = np.arange(-2, 4, 0.05) X, Y = np.meshgrid(X, Y) Z = np.exp(-(np.power(X,2)+np.power(Y,2)))+2*np.exp(-(np.power(X-1.7,2)+np.power(Y-1.7,2))) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot') plt.show()
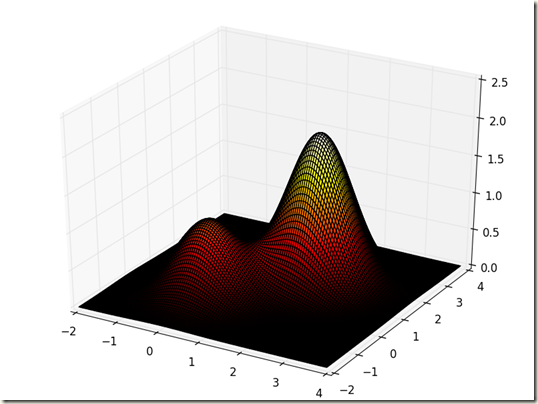
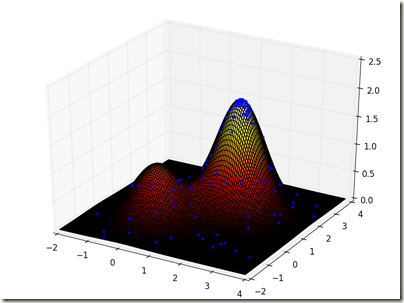
生成的图像如下:
图 2
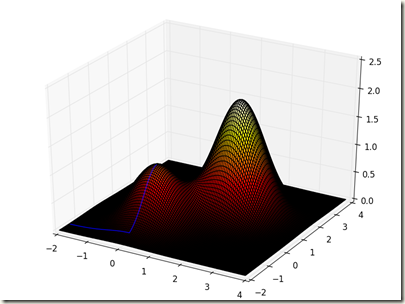
从图像中发现,这个函数具有两座山峰,一高一矮,然后我们写一个爬山算法,基本思路为:先随机选择一个起点,从此点开始登山,依次寻找该点四周的点,判断是否比此点高,不断循环,直到四周没有比其更高的点为止,此时找到的点即为最优解(最大值)。
使用Python写一个爬山函数
def argmax(stx, sty, alisx=0, alisy=0): cur = func(stx, sty) next = func(alisx, alisy) return cur < next and True or False def climb(X,Y): global_X = [] global_Y = [] len_x = len(X) len_y = len(Y) # 随机登山点 st_x = random.randint(0, len_x-1) st_y = random.randint(0, len_y-1) while (len_x > st_x >= 0) or (len_y > st_y >= 0): if st_x + 1 < len_x and argmax(X[0][st_x], Y[st_y][0], X[0][st_x +1],Y[st_y][0]): st_x += 1 elif st_y + 1 < len_x and argmax(X[0][st_x], Y[st_y][0], X[0][st_x +0], Y[st_y + 1][0]): st_y += 1 elif st_x >= 1 and argmax(X[0][st_x], Y[st_y][0], X[0][st_x -1],Y[st_y][0]): st_x -= 1 elif st_y >= 1 and argmax(X[0][st_x], Y[st_y][0], X[0][st_x +0], Y[st_y - 1][0]): st_y -= 1 else: break global_X.append(X[0][st_x]) global_Y.append(Y[st_y][0]) return global_X, global_Y, func(X[0][st_x], Y[st_y][0])
调用此爬山函数,并把爬山路径描绘出来
px, py, maxhill = climb(X, Y) print maxhill ax.plot(px,py,func(np.array(px),np.array(py)),'b')
通过多次运行脚本,得到的以下几种可能的图像(因为是随机值,你在本地运行的爬山路径具体可能不一样)
| 序号 | 图像 | 最大值 |
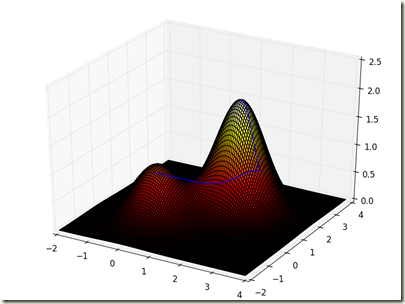
| 1 | 2.00308871541 | |
| 2 | 2.00308871541 | |
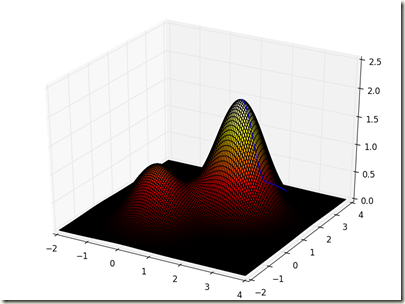
| 3 | 1.00617743082 |
从上面表格中序号为3的图中,能够清楚的看到,爬山的路径不一定会爬到最高的山顶(全局最优解),有可能会爬到局部的山顶(局部最优解),所以这种算法存在这种缺陷。聪明的科研人员提出了一种改进这种算法的方法,当当当……,下面就有请模拟退火算法登场。
3.模拟退火算法基本思想
模拟退火(simulated annealing SA)算法的思想最早是由Metropolis等提出的,其出发点是基于物理中固体物质的退火过程与一般问题的组合优化问题的相似性。其物理过程由三部分组成:
(1)加温过程。使粒子加强运动,使其偏离平衡位置。当温度足够高时,固体变为液体,从而消除系统原先存在的非均匀状态。
(2)等温过程。温度不变,系统状态的自发变化朝自由能减少的方向进行,当自由能达到最小时,保持平衡。
(3)冷却过程。使粒子热运动减弱,系统能量降低,得到晶体结构。
通俗的讲就是:温度越高,出现一次能量差的降温的概率就越大;温度越低,则出现降温的概率就越小。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。以图1为例,模拟退火算法在搜索到局部最优解A后,会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点,于是就跳出了局部最大值A。
关于爬山算法与模拟退火,有一个有趣的比喻:
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
SA算法实现过程:
(1)初始化:取初始温度T0足够大,令T=T0.随机取一个值,得初始解S1,确定每个T时的迭代数,即Metropolis链长L。
(2)对当前温度T和k=1,2……,L,重复步骤(3)-(6)
(3)对当前解S1随机产生一个新解S2
(4)计算S2的增量df=f(S2)-f(S1),其中f(S1)为S1的代价函数
(5)若df<0,则接受S2作为新的当前解,即S1=S2;否则计算S2的接受概率exp(-df/T),即随机产生(0,1)区间上均匀分布的随机数rand,若exp(-df/T)>rand,也接受S2作为新的当前解,S1=S2;否则保留当前解S1
(6)如果满足终止条件Stop,则输出当前解S1作为最优解,结束程序。终止条件Stop通常为:在连续若干个Metropolis链中新解S2都没有被接受时,终止算法;或者设定的温度结束。否则继续按衰减函数衰减T后返回步骤(2)。
4.模拟退火算法案例与实现
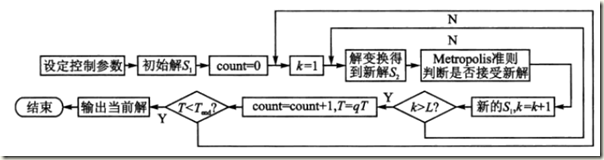
4.1 算法流程
流程图中Metropolis准则为:
如果df<0,以1的概率接受值,否则,以概率exp(-df/T)的概率接受新的值。
4.2 算法Python实现
def climb_SA(X,Y): global_X = [] global_Y = [] # 初始温度 temperature = 105.5 # 温度下降的比率 delta = 0.98 # 温度精确度 tmin = 1e-10 len_x = len(X) len_y = len(Y) # 随机登山点 st_x = X[0][random.randint(0, len_x - 1)] st_y = Y[random.randint(0, len_y-1)][0] st_z = func(st_x, st_y) while (temperature > tmin): # 随机产生一个新的邻近点 # 说明: 温度越高,邻近点跳跃的幅度越大 tmp_x = st_x + (random.random() * 2 - 1) * temperature tmp_y = st_y + + (random.random() * 2 - 1) * temperature if 4 > tmp_x >= -2 and 4 > tmp_y >= -2: if argmax(st_x, st_y, tmp_x, tmp_y): st_x = tmp_x st_y = tmp_y else: # 有机会跳出局域最优解 pp = 1.0 / (1.0 + np.exp(-(func(tmp_x, tmp_y) - func(st_x, st_y)) / temperature)) if random.random() < pp: st_x = tmp_x st_y = tmp_y temperature *= delta # 以一定的速率下降 global_X.append(st_x) global_Y.append(st_y) return global_X, global_Y, func(st_x, st_y)
调用此模拟退火算法函数,并把点描绘出来:
px,py,maxhill = climb_SA(X,Y) print maxhill ax.plot(px,py,func(np.array(px),np.array(py)),'b.')
通过运行脚本:
打印的结果为:2.00264256484
再次运行
打印的结果为:2.00063593674
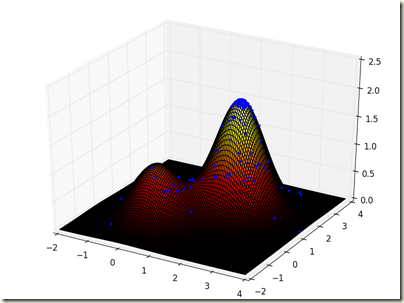
这样多次运行,观察发现,山顶处汇聚了大量的点,山脚下散落着少量的点,最终基本都能得到问题的近似最优解。
5.算法评价
模拟退火算法是一种随机算法,并不一定能找到全局的最优解,可以比较快的找到问题的近似最优解。 如果参数设置得当,模拟退火算法搜索效率比穷举法要高。但是,模拟退火算法其实就是靠大数定律才成立的一个方法,初始解和产生新解,判断新解是否能够接受都是靠随机数,都是靠概率,所以期间就会产生大量的解,当问题的规模不断变大的时候,要想得到质量高的解,搜索的解的数目就会指数级的增加,无限膨胀算法的计算时间。后续可考虑将算法的寻优过程由串行改为并行。