[DeeplearningAI笔记]第二章1.10-1.12梯度消失,梯度爆炸,权重初始化
觉得有用的话,欢迎一起讨论相互学习~
1.10 梯度消失和梯度爆炸
-
当训练神经网络,尤其是深度神经网络时,经常会出现的问题是梯度消失或者梯度爆炸,也就是说当你训练深度网络时,导数或坡度有时会变得非常大,或非常小,甚至以指数方式变小.这加大了训练的难度.
-
假设你正在训练一个很深的神经网络,并且将其权重命名为"W[1],W[2],W[3],W[4]......W[L]"

-
为了简化说明,我们选择激活函数为g(z)=z(线性激活函数),b[l]=0(即忽略偏置对神经网络的影响)
-
这样的话,输出
[hat{y}=w[l]*w[l-1]*w[l-2]...w[2]*w[1]*x
]
- 假设每层的W的值相等都为:
[egin{bmatrix}1.5&0\0&1.5\end{bmatrix}
]
- 从技术上讲第一层的权值可能不同,基于此我们有式子
[hat{y}=w[1]*egin{bmatrix}1.5&0\0&1.5\end{bmatrix}^{L-1}*x
]
- 对于一个深层神经网络来说层数L相当大,也就是说预测值(hat{y})实际上是以指数级增长的,它增长的比率是(1.5^L),因此对于一个深层神经网络来说,y的值将爆炸式增长.相反的,如果权重是0.5,有
[hat{y}=w[1]*egin{bmatrix}0.5&0\0&0.5\end{bmatrix}^{L-1}*x
]
因此每个矩阵都小于1,假设x[1]x[2]的输入值都是1,那么激活函数值到最后会变成(0.5^{(L-1)})激活函数值将会以指数级别下降.
-
对于深层神经网络最终激活值的直观理解是,以上述网络结构来看,如果每一层W只比1大一点,最终W会爆炸级别增长,如果只比W略微小一点,在深度神经网络中,激活函数将以指数级递减.
-
虽然只是论述了对于最终激活函数输出值将以指数级别增长或下降,这个原理也适用与层数L相关的导数或梯度函数也是呈指数增长或呈指数递减
-
直观上理解,梯度消失会导致优化函数训练步长变小,使训练周期变的很长.而梯度爆炸会因为过大的优化幅度而跨过最优解
ps: 对于该视频中关于梯度消失和梯度爆炸的原理有一些争论
请参考
1.11 神经网络中的权重初始化
- 对于梯度消失和梯度爆炸的问题,我们想出了一个不完整的解决方案,虽然不能彻底解决问题但却很有用,有助于我们为神经网络更谨慎的选择随机初始化参数
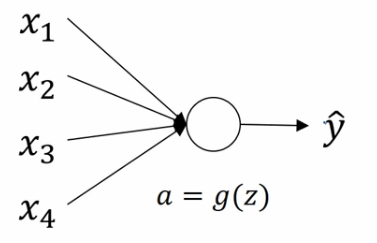
单个神经元权重初始化
-
-
假设神经元有四个特征输入,暂时忽略b对神经元的作用则:
[z=w_{1}x_{1}+w_{2}x_{2}+w_{3}x{3}+...+w_{n}x_{n}
]
-
为了防止梯度爆炸或者梯度消失,我们希望(w_{i})尽可能小,最合理的方法就是设置(W方差为frac{1}{n}) n表示神经元的输入特征数量
-
更简洁的说,如果你用的是Sigmoid函数,设置某层权重矩阵
[W^{[l]}=np.random.randn(shape)*np.sqrt(frac{1}{n^{[l-1]}})(该层每个神经元的特征数量分之一,即l层上拟合的单元数量)
]
-
如果你用的是ReLU激活函数,设置方差为(frac{2}{n})更好,更简洁的说,就是设置某层权重矩阵
[W^{[l]}=np.random.randn(shape)*np.sqrt(frac{2}{n^{[l-1]}})(该层每个神经元的特征数量分之一,即l层上拟合的单元数量)
]
-
如果你用的是Tanh激活函数,则设置某层权重矩阵为
[W^{[l]}=np.random.randn(shape)*np.sqrt(frac{1}{n^{[l-1]}})
]
或者为
[W^{[l]}=np.random.randn(shape)*np.sqrt(frac{2}{n^{[l-1]}+n^{l}})
]
-
这些方法都被成为Xavier 初始化(Xavier initialization),实际上,NG认为所有这些公式都只是给你一个起点,它们给出初始化权重矩阵的方差的默认值,如果你想添加方差,则方差参数则是另一个你需要调整的超级参数,例如对于ReLU激活函数而言,你可以尝试给公式
[W^{[l]}=np.random.randn(shape)*np.sqrt(frac{2}{n^{[l-1]}})
]
添加一个乘数参数,但是NG认为相对于其他参数的调优,通常把它的调优优先级放得比较低.
1.12 梯度的数值逼近
主要讲利用双边误差计算公式:
[frac{f( heta+epsilon)-f( heta-epsilon)}{2epsilon}approx{g( heta)}
]
利用这个公式简单的估计函数的微分.



