在求线性方程组时，其系数及它们各自的位置是非常重要的，在进行变化时，必须保持各方程的排列次序，因而我们常常将未知数的系数排成一个矩形的数表。
例如：线性方程组
将其系数按照方程组中原有的相应位置排成一个矩形数表如下：
，
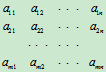我们称这样的矩形数表为矩阵。
定义1 由m´n个数aij(i=1, 2, × × × , m; j=1, 2, × × ×, n)排成的m行n列的矩形数表
称为m´n阶矩阵,一般情况下, 我们用大写字母A, B, C等表示矩阵，并记作
,
矩阵中的m´n个数称为矩阵的元素，所有元素及相应位置是个整体，所以，要加一个方括号表示它。
矩阵A中m个横的n元组[a11，a12，…， a1n]，[a21，a22，…， a2n]，…，[am1，am2，…， amn]称为矩阵的行；n个竖的m元组
称为矩阵的列。
aij称为矩阵的第i行第j列的元素. A中有m´n个元素，所以m´n矩阵A也可表示为A=(aij)m´n 或记作A m´n .例如
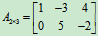
表示一个具有2行3列6个元素的矩阵
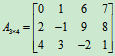
表示一个具有3行4列12个元素的矩阵
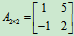
表示一个具有2行2列4个元素的矩阵
若矩阵A的行数与列数都等于n, 则称A为n阶矩阵, 或称为n阶方阵. n阶矩阵A也记作An .
n阶矩阵与n阶行列式从形式上看只有一点区别，前者是用括号把n的平方个数括起来，是一个数表，后者是用两条竖线把n的平方个数围起来，具有n!项的复杂的展开式，代入具体的元素数值，算出来是一个确定的数
只有一行的矩阵即m=1时，A=(a1 a 2 × × × an)称为n元行矩阵, 或称为n维行向量. 行矩阵也记作
A=(a1, a 2, × × × , an).
只有一列的矩阵
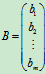
称为m元列矩阵, 或称为m维列向量.
矩阵中的元素都是实数时，称为实矩阵，矩阵中的所有元素均为0的矩阵称为零矩阵, 记为O.
两个矩阵的行数相等、列数也相等, 就称它们是同型矩阵. 如果A=(aij)与B=(bij)是同型矩阵, 并且 它们的对应元素相等, 即
aij=bij(i=1, 2, × × ×, m; j=1, 2, × × ×, n),
则称矩阵A与矩阵B 相等, 记作A=B.
如：若
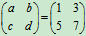
则a=1,b=3,c=5,d=7。
注意：不同型的零矩阵是不相等的。
研究变量间的线性变换时，可将线性变换与矩阵对应起来。
设n个变量x1, x2, × × ×, xn与m个变量y1, y2, × × ×, ym之间的关系式
表示一个从变量x1, x2, × × ×, xn到变量y1, y2, × × ×, ym的线性变换, 其中aij为常数. 线性变换的系数aij构成矩阵A=(aij)m´n,即
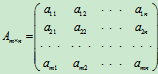
称为系数矩阵.
给定了线性变换, 它的系数所构成的矩阵也就确定了. 反之, 如果给出一个矩阵作为线性变换的系数矩阵, 则线性变换也就确定了. 在这个意上, 线性变换与矩阵之间存在着一一对应的关系.矩阵A可以反映线性变换的特点。
如果对应一个恒等变换
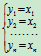
它对应的系数矩阵是一个n阶方阵
.
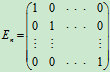这种方阵的特点是：主对角线上的元素全部是1，其它元素都是0，我们称这样的矩阵为n阶单位矩阵, 简称单位阵. 通常记作En，反之，一个单位矩阵对应的线性变换一定是个恒等变换。
线性变换
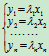
对应的n阶方阵
.
这种方阵称为对角矩阵, 简称对角阵. 对角阵也记作
L=diag(l1, l2, × × ×, ln).
如果将变量组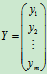
看成一个m列矩阵，将将变量组
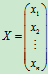看成一个n元列矩阵，由矩阵的乘法运算可将线性变换表示为Y=AX。
同样地，在研究线性方程组的求解问题中可将线性方程组
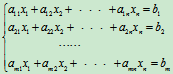
表示为Ax=b
，
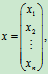
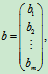
A称为系数矩阵。
我们将在下一章讨论矩阵A的性质与线性方程组解的关
系。
