1.冒泡与选择
冒泡:冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个数据进行比较,如果前者比后者大,就互相交换,最后就会找到一个最大的落在数组最后.重复以上工作n次即可完成排序.
void BubbleSort(vector<int> a)
{
int len = a.size();
if (len <= 1)
return;
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len - i - 1; j++)
{
if (a[j + 1] < a[j])
std::swap(a[j], a[j + 1]);
}
}
}
- 时间复杂度:平均时间复杂度O(n^2).
- 空间复杂度O(1).原地排序
- 是否稳定:稳定
选择:每次找到最小的一个元素放到已经排好序的数组的尾部即可.
void SelectSort(vector<int> a)
{
int len = a.size();
if (len <= 1)
return;
for (int i = 0; i < len; i++)
{
for (int j = i + 1; j < len; j++)
{
if (a[j] < a[i])
std::swap(a[j], a[i]);
}
}
}
2.插入
就是将后面的数据与前面的数据进行相比,如果小的话就将前面的数据向后移动,然后将其插入即可.
void InsertSort(vector<int> &a)
{
int len = a.size();
if (len <= 1)
return;
for (int i = 1; i < len; i++)
{
int key = a[i];
int j = i - 1;
/*查找插入的位置*/
for (; j >= 0; j--)
{
if (a[j] > key)
a[j + 1] = a[j]; /*数据移动*/
else
break;
}
a[j + 1] = key; //数据插入
}
}
- 时间复杂度:平均时间复杂度O(n^2).因为我们在一个数组中插入数据是O(n),最坏也是n的平方
- 空间复杂度O(1).原地排序
- 是否稳定:稳定
3.快排
快排的思想就是"分而治之".找到一个分区点,然后将小的放在前面,大的放在后面,分区点放在中间.最后发现待排序的区间变为1时停止.
/*在这个函数中会改变原数组,见下图:*/
/*从头到尾迭代,和支点比较,大的不管,小的换。换了才往后看。最后支点戳中间,算是分界线*/
int partition(vector<int> &a, int l, int r)
{
int k = l, pivot = a[r];
int temp = 0;
for (int i = l; i < r; i++)
{
if (a[i] <= pivot) /*相等的元素要么放右边,要么放左边,这里也可以放在右边*/
{
std::swap(a[i], a[k++]);
}
}
std::swap(a[k], a[r]);
return k;
}
/*快速排序递归函数*/
void quick_sort(vector<int> &a, int l, int r)
{
if (l >= r)
return;
int q = partition(a, l, r); /*获取分区点*/
quick_sort(a, l, q - 1);
quick_sort(a, q + 1, r);
}
void QuickSortWithRecursive(vector<int> &a)
{
quick_sort(a, 0, a.size() - 1);
}
其中经过partition函数分区之后,数组就会变成这样.partition 在一般情况下会选择以数组的尾巴为分界线
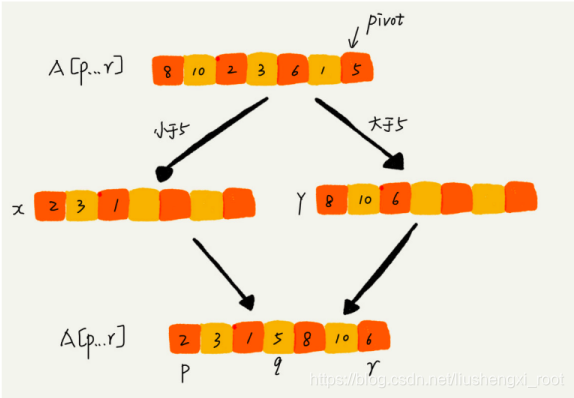
- 时间复杂度:大多数情况下时间复杂度O
(nlog(n)).极少数情况下,效率是O(n^2).(所谓的优化其实就是将这个概率不断降低) - 空间复杂度O(1).原地排序
- 是否稳定:不稳定
4. 拓扑排序(与图有关,图用(逆)邻接表存储)
我们先来看一个生活中的拓扑排序的例子。
我们在穿衣服的时候都有一定的顺序,我们可以把这种顺序想成,衣服与衣服之间有一定的依赖关系。比如说,你必须先穿袜子才能穿鞋,先穿内裤才能穿秋裤。假设我们现在有八件衣服要穿,它们之间的两两依赖关系我们已经很清楚了,那如何安排一个穿衣序列,能够满足所有的两两之间的依赖关系?
这就是个拓扑排序问题。从这个例子中,你应该能想到,在很多时候,拓扑排序的序列并不是唯一的。你可以看我画的这幅图,我找到了好几种满足这些局部先后关系的穿衣序列。

拓扑排序的一个经典问题就是"如何确定代码源文件的编译依赖关系?"什么是依赖关系,这个就不属于本文讨论范畴了.那么该如何解决呐?
我们可以把源文件与源文件之间的依赖关系,抽象成一个有向图。每个源文件对应图中的一个顶点,源文件之间的依赖关系就是顶点之间的边。 如果 a 先于 b 执行,也就是说 b 依赖于 a,那么就在顶点 a 和顶点 b 之间,构建一条从 a 指向 b 的边。而且,这个图不仅要是有向图,还要是一个有向无环图,也就是不能存在像 a->b->c->a 这样的循环依赖关系。因为图中一旦出现环,拓扑排序就无法工作了。实际上,拓扑排序本身就是基于有向无环图的一个算法。
OK ,现在我们有思路了,但是我们如何实现拓扑排序呐?这里有两种方法:
(1)Kahn 算法
Kahn 算法实际上用的是贪心算法思想,思路非常简单、好懂。
定义数据结构的时候,如果 s 需要先于 t 执行,那就添加一条 s 指向 t 的边。所以,如果某个顶点入度为 0, 也就表示,没有任何顶点必须先于这个顶点执行,那么这个顶点就可以执行了。
我们先从图中,找出一个入度为 0 的顶点,将其输出到拓扑排序的结果序列中(对应代码中就是把它打印出来),并且把这个顶点从图中删除(也就是把这个顶点<指向的顶点的入度>都减 1)。我们循环执行上面的过程,直到所有的顶点都被输出。最后输出的序列,就是满足局部依赖关系的拓扑排序。
(2)DFS 算法
首先,我们去思考DFS算法的思想,递归,从开始到结束,再从结束到上一步.那么我们邻接表是否适合?答案不适合,应该用逆邻接表.具体看代码解释:
#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
#include <queue>
// 如果点的表示还需要插入等操作的话,就将vector 改为 std::list
using namespace std;
class Graph
{
public:
Graph(int v)
{
this->v = v;
for (int i = 0; i < v; i++)
adj.push_back(std::list<int>());
}
void AddEdge(int s, int t)//s->t
{
adj[s].push_back(t);
}
void TopSortByKahn()
{
vector<int> inDegree(v, 0); //统计每个顶点的入度
for (int i = 0; i < v; i++)
{
for (auto t : adj[i])
{
inDegree[t]++;
}
}
queue<int> que;
for (int i = 0; i < v; i++)
{
if (inDegree[i] == 0)
que.push(i);
}
while (!que.empty())
{
int head = que.front();
que.pop();
cout << "->" << head;
for (auto t : adj[head])
{
inDegree[t]--;
if (inDegree[t] == 0)
que.push(t);
}
}
}
void TopSortByDFS()
{
// 先构建逆邻接表
std::vector<std::list<int>> inverseadj(v, std::list<int>());
for (int i = 0; i < v; i++) // 通过邻接表生成逆邻接表
{
for (auto t : adj[i])
{
inverseadj[t].push_back(i);
}
}
bool visted[v] = {false};
for (int i = 0; i < v; i++) //dfs
{
if (visted[i] == false)
{
visted[i] = true;
dfs(i, inverseadj, visted);
}
}
}
private:
void dfs(int vertex, const std::vector<std::list<int>> &inverseadj,
bool visted[])
{
// cout << vertex << endl;
for (auto t : inverseadj[vertex])
{
if (visted[t] == true)
continue;
else
{
visted[t] = true;
dfs(t, inverseadj, visted);
}
}// 先把 vertex "这个顶点依赖的所有顶点"都打印出来之后,再打印它自己(核心)
cout << "->" << vertex;
}
private:
int v; //顶点个数
std::vector<std::list<int>> adj; //邻接表
};
int main(void)
{
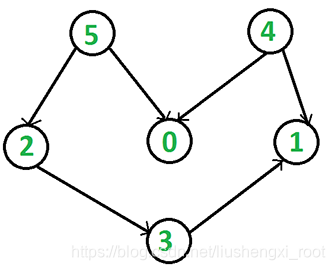
Graph g(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
g.TopSortByKahn();
cout << endl;
g.TopSortByDFS();
cout << endl;
return 0;
}
所使用的图是: