学习第一类斯特林数小记

定义

首先它有两个概念——
1、考虑的是组合数概念（无符号的斯特林数）
$S(n,m)$表示把n个不同的球放入m个相同的盒子中，不允许有空盒的方案，而且注意，这个盒子很有意思，这些球只能放成一圈且如果顺序不同也视为不同方案。
2、考虑的是表现升阶函数和降阶函数的各项系数的概念（分为有无符号的斯特林数）
有符号斯特林数表示为$S_s$反之表示为$S_u$
$x^{n↓}=x(x-1)(x-2)……(x-n+1)=sum_{k=0}^n S_s(n,k)x^k$
$x^{n↑}=x(x+1)(x+2)……(x+n-1)=sum_{k=0}^n S_u(n,k)x^k$
（注意，这个升阶函数可以表示为排列数$P_x^n$）
至于如何理解上面两者概念之间的共性。
我有一个方法，不知道对不对。
由于考虑把升阶函数或降阶函数分解并且表达成为一个$系数*x^k$的形式。
所以就可以画出一个树状图然后去把x某个次方分门别类。
类似于这样——

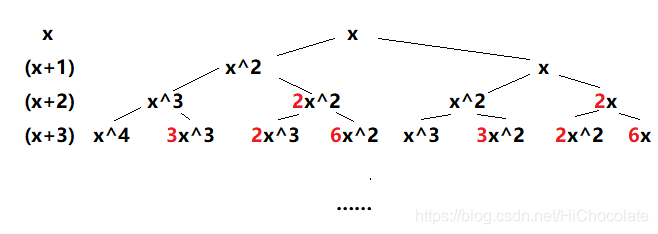
把系数合并合并。
于是系数就很像是上面的第一个概念推出来的数了。
至于为什么像，我们可以看到下面的递推式子再来理解。

递推式

我们可以看到百度百科，写得很清楚。
于是我就不怎么严谨地口胡一下。
第一个概念——
我们现在有n个球，放入m个盒子中。
现在要多放入一个球，那么就会有两种情况——
1、我们独自在一个新盒子中放入这个球，于是就从$S(n,m-1)$推过来。
2、由于之前有很多种不同的方案，那么就把这个新的球放在原来任意一个球的左边。
就从$n*S(n,m)$推过来。
$S(n+1,m)=S(n,m-1)+n*S(n,m)$get√
第二个概念——
直接利用定义+归纳法得到递推式：
$sum_{k=0}^{n+1}S(n+1,k)*x^k=x^{n+1↓}=x^{n↓}*(x-n)=x*sum_{k=0}^{n}S(n,k)*x^k-n*sum_{k=0}^{n}S(n,k)*x^k$
依次把$x^m$在左右两边的系数提取出来得：
$S(n+1,m)=S(n,m-1)-n*S(n,m)$
我们发现，这是在有符号的斯特林数中得到的，
故：$S_s(n,m)=(-1)^{n+m}*S_u(n,m)$

有了递推式，然后干嘛？
三角形！！！

“pascal”三角形或杨辉三角形

这个东东也是看百度百科学会的（发现的）
下面这个三角形是根据第一个概念推的。

然后，我们考虑上述的无符号斯特林数。
我们惊奇地发现，这个与我们之前的树状图合并同类项后系数是神似的！！！
那么我们就找到了第一个概念与第二个概念之间的共性。
第二个概念——（可以变化一下）
表示在做树状图时，由于第n层可以使上一层某个数的系数变大或使指数+1.
那么在第n层，指数为m时，
这个可以由上一层指数为m-1的情况乘上一个x变成指数为m的情况。
也可以由上一层指数为m的情况乘上当前（x+n）的这个n得到答案。
也就是在类似于dp转移意义上解释了这个第二个概念，且与第一个概念基本相同。
这样再看这两个概念就感觉很亲近啦~
不必多废话，我们继续看到这个神奇的三角形。

由于我们得到了递推公式以及这个三角形的样子，可以得到各种性质——
自百度百科

其实前几项也并不是特别地有用。
而后面的几项看起来很有用，而我不会用。

举例运用

第一个是经典例题，这里不多讲述。
第二个则是求下面的式子：
$sum_{i=1}^ni^k$
这就是大名鼎鼎的自然数幂的和。
然后开始化式子。
根据定义：
$C_n^k=frac{P_n^k}{k!}=frac{sum_{i=0}^k (-1)^{i+k}*S_s(k,i)n^i}{k!}$
把$n^k$提出来：
$C_n^k*k!=n^k+sum_{i=0}^{k-1} (-1)^{i+k}*S_s(k,i)n^i$
$n^k=C_n^k*k!-sum_{i=0}^{k-1} (-1)^{i+k}*S_s(k,i)n^i$
然后把原来的式子换一下
$sum_{j=1}^nj^k$
套入上述结果，再推：
$sum_{j=1}^n (C_j^k*k!-sum_{i=0}^{k-1} (-1)^{i+k}*S_s(k,i)j^i)$
去括号
$sum_{j=1}^n C_j^k*k!-sum_{j=1}^n sum_{i=0}^{k-1} (-1)^{i+k}*S_s(k,i)j^i$

至此，我们发现推不下去了，那么我们引入一个小小的结论：
$sum_{i=0}^m C_n^i=C_{n+1}^{m+1}$
证明？
$C_{n+1}^{m+1}=C_{n}^m+C_n^{m+1}$
这个很好理解吧？就是分成两种情况，一种是在这个选第m+1个数，第二种是不选。
有了这个东东，带入原式，然后又会发现出现一样的结论，再带入，再看，就可以发现这个结论是对的！

那好，利用这个结论丢入原式。
$C_{n+1}^{k+1}*k!-sum_{i=0}^{k-1}sum_{j=1}^n (-1)^{i+k}*S_s(k,i)j^i$
我们设一个函数$f(n,k)=sum_{i=1}^ni^k$
原式则为：
$C_{n+1}^{k+1}*k!-sum_{i=0}^{k-1}(-1)^{i+k}*S_s(k,i)*f(n,i)$
然后，如果给你取模数，这个模数是质数，则这条式子已经够用了。
但是如果出题人丧心病狂地把这个模数变成任意数，怎么办？
不用方，只需把前面的组合数改一下即可——
$frac {P_{n+1}^{k+1}}{k+1}-sum_{i=0}^{k-1}(-1)^{i+k}*S_s(k,i)*f(n,i)$
然后这个$P=(n+1)(n)(n-1)(n-2)……((n+1)-(k+1)+1)$
然后这是连续的k+1个数，然后这连续的k+1个数中，必然存在一个是k+1的倍数的数。
所以就可以不用关心逆元了。
（听说这玩意可以用第一类斯特林数的同胞第二类斯特林数来求，管它呢！）
时间为$O(k^2*（比较大的常数）)$

母函数？

我不费！
我还是太弱了，听大佬说可以利用这个东东求通项公式。