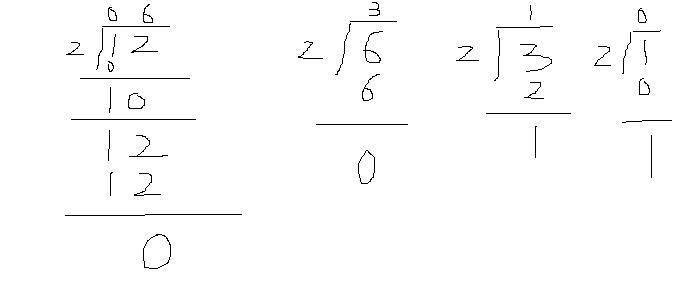1 #include <stdio.h> 2 #include <string.h> 3 4 char str[1000];//输入字符串 5 int start[1000],ans[1000],res[1000]; //被除数,商,余数 6 //res[]存的是余数,其最后结果的逆序为所求的结果 7 //转换前后的进制 8 const int oldBase = 10; 9 const int newBase = 2; 10 11 void change() 12 { 13 //各个数位还原为数字形式 14 int i,len = strlen(str); 15 start[0] = len; 16 for(i=1; i<= len; i++) 17 { 18 if(str[i-1] >= '0' && str[i-1] <= '9') 19 { 20 start[i] = str[i-1] - '0'; 21 } 22 } 23 } 24 //start[0]存的是串的长度,其他元素为被除数的每一位 25 void solve() 26 { 27 memset(res,0,sizeof(res));//余数初始化为空 28 int y,i,j; 29 //模n取余法,(总体规律是先余为低位,后余为高位) 30 while(start[0] >= 1) 31 { 32 //只要被除数仍然大于等于1,那就继续“模2取余” 33 y=0; 34 i=1; 35 ans[0]=start[0]; 36 //从第一位开始处理每一位(被除数=上一轮得到的余数*新的进制数+当前位的数) 37 while(i <= start[0]) 38 { 39 y = y * oldBase + start[i]; 40 ans[i++] = y/newBase; 41 y %= newBase; 42 } 43 res[++res[0]] = y;//这一轮运算得到的余数 44 i = 1; 45 //找到下一轮商的起始处 46 while((i<=ans[0]) && (ans[i]==0)) 47 i++; 48 //清除这一轮使用的被除数 49 memset(start,0,sizeof(start)); 50 //本轮得到的商变为下一轮的被除数 51 for(j = i; j <= ans[0]; j++) 52 start[++start[0]] = ans[j]; 53 memset(ans,0,sizeof(ans)); //清除这一轮的商,为下一轮运算做准备 54 } 55 } 56 void output() 57 { 58 //从高位到低位逆序输出 59 int i; 60 for(i = res[0]; i >= 1; --i) 61 { 62 printf("%d",res[i]); 63 } 64 printf(" "); 65 } 66 67 int main() 68 { 69 scanf("%s",str); 70 change(); 71 solve(); 72 output(); 73 return 0; 74 }
引用原文:
在数据结构课关于栈的这一章中,我们都学过用“模2取余法”来将一个10进制数转换为一个二进制数,进而可以推广到“模n取余法”,经其转换为n进制(n任意指定)。
确实,这是一个很基础的题目,可你是否想过如果这个10进制数是一个大数(其位数可能上千位,此时用一般数据类型肯定是会溢出的),那么这个问题又如何来求解呢?
当然,也许你会说很简单嘛,自己写一个大数类(当然至少要写一个大数除法才行),或者你用的是Java这种现代化语言,就更轻松了,直接用BigInteger这样的大数类就可以来表示一个大数,进而用书上教的方法来实现。
但是,真的需要用到大数类吗?事实上,“杀鸡焉用牛刀“,我们在纸上模拟一番上述运算后就可以发现,只要做一些小小的改进,就可以在不使用大数的情况下,也可以通过“模n取余”的原理来实现大数的进制转换的。(当然,整体的思想仍然是“模n取余”原理!!!)。
举个简单的例子,就比如说把10进制数12转换为2进制形式,书上的方法可以用下图来表示
按照 “先余为低位,后余为高位“这条铁律,其结果为1100.
这是书上教我们的常规思路(可惜按这个的话,大数是没法考虑的,因为假如这里不是12,而是一个1000位的大数,由于是是对大数的整体进行取余运算,不使用大数类及其除法操作,又如何得以进行呢?),可我们的目的是不使用大数类,那么现在我们就来换一个视角来看这个问题,12是一个十位数,十位上是1,个位上是2,按照我们正常的思维来看,这个计算应该是下面这样的:
那么我们发现在第一轮运算时,十位上的1作为被除数,2作为除数,得到的商是0,余数是1(可以断言只考虑当前这一个数位的计算,余数或是0,或是1,若是1的话,则进入下一数位(这里即对个位进行运算)时,要用1乘上进制(这里是10)再加上下一个数位上的值(这里是2)),即得到运算进入个位时被除数是12,除数是2,得到的商是6,余数是0。第一轮运算的结果是商是06,余数是0.
进入第二轮运算,则上一轮的商6(这里首先要去掉前面多余的0)变成本轮的被除数,如此下去,即可得到每轮的余数。
推广开来,如果被除数是一个1000位的大数,例如“12343435154324123……342314324343”
那么我们照样可以从第一个数位开始逐位考虑,比如第一位是1(作为被除数),2是除数,得到的商是0,余数是1,然后是第二个数位2,由于上一位留下了余数1,则此时被除数应该是1*10+2 = 12,所以得到的商是6,余数是0,即运算到此时的商是06,然后是第三个数位3,由于上一个数位留下的余数是0,所以此时被除数就是3,。。。如此下去就完成第一轮的运算,
这一轮完毕后,需要把得到的商变成下一轮的被除数,继续上述的运算,直到被除数为0才停止。
下面给出了一个示例代码,展示了如何将一个10进制的大数转换为其二进制形式,仅供参考:(注释很详细)