题目大意
有$n$块拼图,每一块都由左中右三个部分组成,每块拼图中间部分是高为$H$的长方形,对于第$i$块品推左侧是高为$A_i$距离底部为$C_i$的长方体,右侧是高位$B_i$距底部为$D_i$的长方体。
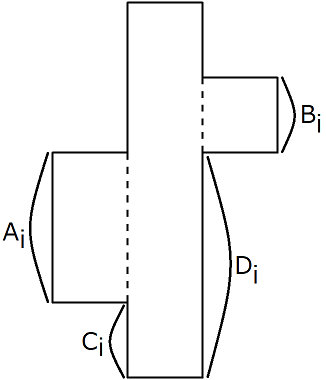
其中每块拼图每个部分都是等宽的
现在让你将这$n$个拼图一次摆在一条直线上方,满足每块拼图中部底端要紧贴直线,并且直线以上不存在一个区域,使得该区域没有被拼图覆盖且该区域上方有区域被拼图覆盖。
$nleq 10^5,Hleq 10^5$
题解
神仙题。
由于这道题只关心,每一块左右部分与地面直线相邻的部分是空还是实心的,并且有多高。
一侧高为$k$的实心可以和另一侧高位$k$的空心相接,不妨把这看作是一个点。
设左侧高为$k$的实心或右侧高位$k$的空心是标号为$-k$的点。
设左侧高为$k$的空心或右侧高位$k$的实心是标号为$k$的点。
把每块积木看做是一条有向边,于是问题转化为能否找到若干条路径$(S ightarrow T)$,使得$S<0,T>0$。
那么对于每一个点$x$,记它的入度出度为$I_x,O_x$,它要么被经过$(I_x++,O_x++)$,要么作为起点或终点之一$I_x++(x>0)$或$O_x++(x<0)$。
所以若方案可行,一定满足对于所有的点
当$x<0$时,$I_xleq O_x$。
当$x>0$时,$I_xgeq O_x$。
此外,对于每一个若连通分量,至少有一个起点和一个终点,而出现起点就一定会出现终点,所以只需要再特判每一个包含至少一条边的若弱连通分量中出现一个$I_x e O_x$的点即可。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 500
using namespace std;
int read(){
int nm=0,fh=1; int cw=getchar();
for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
return nm*fh;
}
int n,m,e1,e2,h1,h2,cnt,in[M],ot[M],f[M]; bool vs[M];
int fd(int x){return x==f[x]?x:f[x]=fd(f[x]);}
int main(){
n=read(),m=read();
for(int i=1;i<=m;i++) f[i]=i,f[i+m]=i+m,vs[i]=vs[i+m]=false;
for(int i=1;i<=n;i++){
h1=read(),h2=read(),e1=read(),e2=read();
int t1=e1>0?e1:-h1,t2=e2>0?-e2:h2; t1+=m,t2+=m;
if(fd(t1)!=fd(t2)) f[fd(t1)]=fd(t2); in[t2]++,ot[t1]++;
}
for(int i=-m;i<0;i++) if(in[i+m]>ot[i+m]){puts("NO");return 0;}
for(int i=1;i<=m;i++) if(in[i+m]<ot[i+m]){puts("NO");return 0;}
for(int i=0;i<=m+m;i++) if(in[i]!=ot[i]) vs[fd(i)]=true;
for(int i=0;i<=m+m;i++) if(in[i]&&ot[i]&&!vs[fd(i)]){puts("NO");return 0;}
puts("YES"); return 0;
}