Unsupervised Feature Learning via Non-Parametric Instance Discrimination

Wu Z., Xiong Y., Yu S. & Lin D. Unsupervised Feature Learning via Non-Parametric Instance Discrimination. arXiv preprint arXiv 1805.01978

概

这篇文章也是最近很虎的contrastive learning的经典之作, 其用于下游任务的处理虽没现在的简单粗暴, 但效果依然很好.

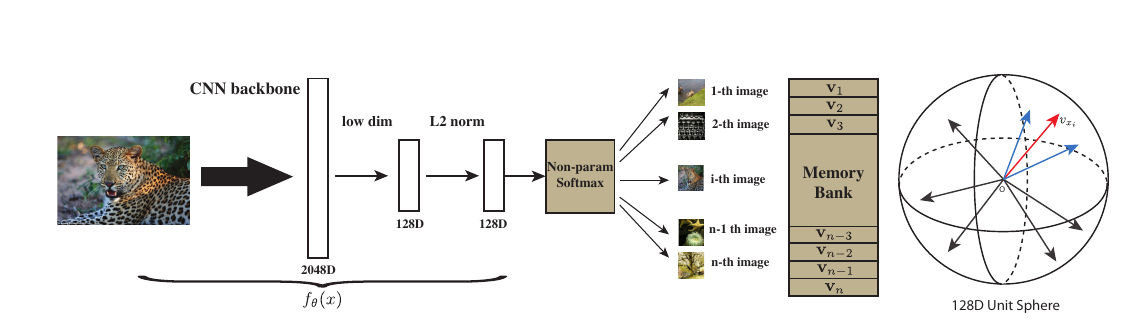
因为作者实际上是从一个无监督的角度去考虑的, 其出发点就是, 如果希望将分类器将每一个样本都区分开来, 是否能够获得比较好的特征呢? 输入(x)经过embedding function 得到(f_{ heta}(x)), 即特征, 那么现在的问题是:

[P(i|x) = frac{exp (w_i^T f_{ heta}(x))}{sum_{i=1}^n exp (w_j^T f_{ heta}(x))}, ]

则最后一个分类层的权重(W in mathbb{R}^{k imes n}), 这将是无法承受的存储量和计算量.

为了解决这个问题, 作者选择的首先构造一个memory bank, 将特征存储起来, 第(i)个样本对应的为(v_i), 而当前(f_{ heta}(x_i))记作(f_i), 则

[P(i|x) = frac{exp (f_{ heta}(x)^Tv_i/ au)}{sum_{j=1}^nexp(f_{ heta}(x)^T v_j / au)}, ]

这里( au)是temperature.

这样就避免了(w), 且符合直觉: 即衡量了(f_{ heta}(x))与数据中的第(i)个样本的相关度. 但是, 虽然这一定程度上减少了存储量, 但是计算量并没有减少, 即我们需要估计分母(Z_i), 实际上, 这就是一个配平的问题, 这是负样本采样可以发挥作用的地方.

假设

[h(i, v) := P(D=1|i,v) = frac{P(i|v)}{P(i|v)+m P_n(i)}, ]

其中(P_n(i))为一个均匀分布, 即每个特征被选中的概率为(frac{1}{n}). 然后便是经典的损失

[mathcal{J}_{NCE} ( heta) = -mathbb{E}_{P_d} [log h(i, v)] - m cdot mathbb{E}_{P_n}(log (1 -h(i,v'))). ]

个人感觉: (P_d(i, v) = P(v) cdot Q(i|v)), 其中(Q(i|v))仅当(v)为第(i)个样本点的特征是概率为(1)否则为(0). 而(P_n(i, v) = P(v) cdot frac{1}{n}). 同时, 估计

[Z_i approx frac{n}{m} sum_{k=1}^m exp(v_{jk}^T f_i/ au), ]

感觉就像是一个抽样. 这个(frac{n}{m})最新的文章里出现过, 但是当时没感觉出其意义来, 原来源头是在这?

解决了计算了和存储问题, 还有一个训练不稳定的问题要解决.

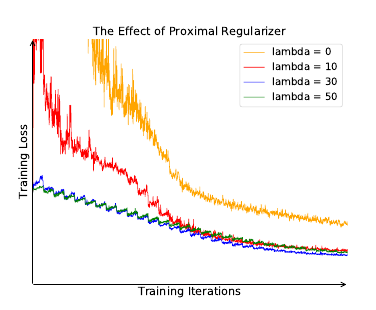
训练不稳定的诱因, 作者认为是每个样本作为一个类, 如此每个类在每个epoch里仅会被访问一次. 解决策略是用proximal 算子:

[mathcal{J}_{NCE}( heta) = -mathbb{E}_{P_d} [log h(i, v^{(t-1)})-lambda |v^{(t)}-v^{(t-1)}|] - m cdot mathbb{E}_{P_n}(log (1 -h(i,v'))). ]

有疑问的是, 我看的proximal算法里面, 应该是(log h(i, v^{(t)})), 虽然二者可能相差不大.