树相关
二叉树(Binary Tree)
几个简单概念
- 满二叉树:除了叶子节点外,每个节点都有左右子节点,叶子节点都在最底层/
- 完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大
Tip:之所以把完成二叉树拎出来,是因为在二叉树的实现中,有链式和数组俩种方式,完全二叉树在数组实现上只浪费一个下标为0的空间,(左右节点等于根节点*2(右要+1))而不是完全二叉树,会有很多额外的空间没用上
二叉查找树(Binary Search Tree)
概念:二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值
查找操作:首先,我们看如何在二叉查找树中查找一个节点。我们先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
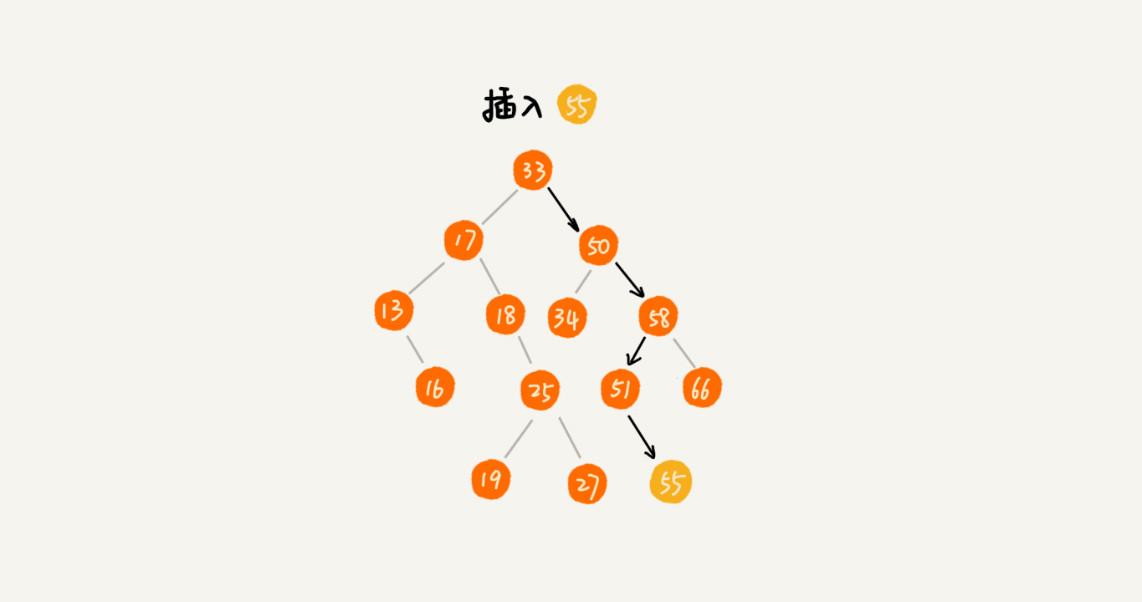
插入操作:二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
删除操作:二叉查找树的查找、插入操作都比较简单易懂,但是它的删除操作就比较复杂了 。针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。
- 第一种情况是,如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
- 第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
- 第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。

还有一个重要的特性,当中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是O(n),非常高效,所以二叉查找树也叫二叉排序树。
实际开发中,我们在二叉树中存储的可能是一个包含很多字段的对象,我们利用对象的某个字段作为键值(key)来构建二叉树,其他字段叫做卫星数据。
不管操作是插入、删除还是查找,时间复杂度都和树的高度成正比,也就是O(height)。平衡二叉树高度接近logn,所以插入、删除、查找操作的时间复杂度比较稳定,是O(logn)。
红黑树
平衡二叉查找树,严格定义是这样的,二叉树任意节点的左右子树高度相差不大于1,第一个被发明出来的平衡二叉树是AVL树。
很多平衡而擦汗书没有严格符号,比如红黑树,它从根节点到各个叶子节点的最长路径,有可能会比最短路径大一倍。
发明平衡二叉树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现的复杂度退化的问题。所以,平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
概念:
·根节点是黑色的;
·每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
·任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
·每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
//红色节点删除之后,有些节点就没有父节点了,它们会直接拿这些节点的祖父节点(父节点的父节点)作为父节点。所以,之前的二叉树就变成了四叉树。
//前面红黑树的定义里有这么一条:从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。我们从四叉树中取出某些节点,放到叶节点位置,四叉树就变成了完全二叉树。所以,仅包含黑色节点的四叉树的高度,比包含相同节点个数的完全二叉树的高度还要小。上一节我们说,完全二叉树的高度近似 log2n,这里的四叉“黑树”的高度要低于完全二叉树,所以去掉红色节点的“黑树”的高度也不会超过 log2n。
我们现在知道只包含黑色节点的“黑树”的高度,那我们现在把红色节点加回去,高度会变成多少呢?从上面我画的红黑树的例子和定义看,在红黑树中,红色节点不能相邻,也就是说,有一个红色节点就要至少有一个黑色节点,将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过 log2n,所以加入红色节点之后,最长路径不会超过 2log2n,也就是说,红黑树的高度近似 2log2n。

//红黑树实现