一、题目
二、解法
首先把转图论模型:有 (20) 个点,按时间顺序往里面加边,要求 (forall i,A_i) 到 (B_i) 有一条时间单调递增的路径,问最小加边数量。这个模型成立的原因是我们按时间顺序操作,如果一个点达到了目标状态就可以把它固定下来。
记 (G_1) 为加边之后形成的图,(G_2) 为连有向边 ((A_i,B_i)) 形成的图;记 (S) 为 (G_2) 最大的 ( t DAG)((m=|S|)),(e) 表示最小边数,(n) 表示总点数,(c) 表示 (G_2) 的弱联通图数量。
Lamma:(e=2n-m-c)
首先证明可以构造到这个答案,考虑把 (S) 中的点按拓扑序重编号为 (1,2...m),那么像这样连边:
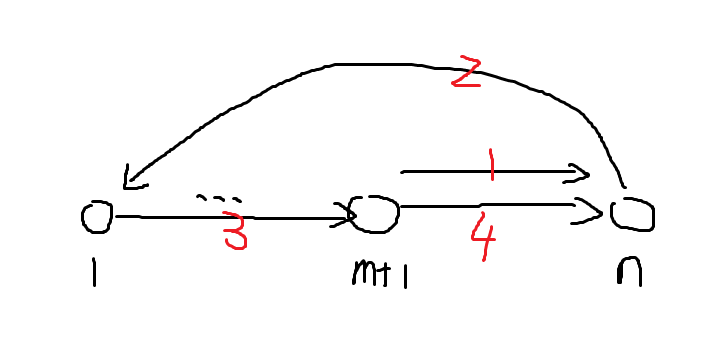
除了 (S) 中满足 (i>j) 的 (i) 无法到 (j) 以外,其他点对都可以互相到达,但因为 (S) 是拓扑图所以并不要求这样的点对有路径。对于这个弱联通块答案是 (e=m+1-2(n-m-1)=2n-m-1),多个弱连通图的答案是 (e=2n-m-c)
然后证明它是答案下界,我们考虑 (G_1) 的任意一种连边方案,维护一个 (G_2) 中的集合 (T),(T) 中没有在 (G_1) 中自己经过时间递增的路径走回自己的点,考虑增量法加边:
- 如果加入的边 ((u,v)) 对应 (G_2) 中的两个弱联通块,那么合并这两个弱联通块,弱联通块个数减 (1)
- 如果加入的边 ((u,v)) 在同一个弱联通内,最坏情况下会使 (T) 中某个点存在时间递增的走回自己的路径,我们可以从 (T) 中去掉 (v) 来保持原有的性质,此时 (T) 的大小至多减 (1)
考虑最优连边方案 (G_1,G_2) 弱联通块个数相等,所以第一种情况的边恰好有 (n-c) 条,根据第二种情况最后 (T) 集合的大小来列不等式:(|T|geq n-(e-(n-c)) ightarrow egeq 2n-|T|-c),取 (|T|=m) 即可证明原结论。
那么现在的问题是求一个最大导出子图使其为 ( t DAG),每次考虑加入一个点,然后出边不连接到原集合即可,也就是我们按拓扑序来规划每个可能的导出子图,那么使用状压 (dp) 可以做到 (O(2^nn))
三、总结
建立图论模型需要积累各种量的意义,本题路径的意义表示一种转化方式。
证明答案下界的思路也很重要,本题用到的方法我称之为势能法,也就是我们找到某个量为势能,对于任意一种决策方案,考虑最坏情况让势能的减少量,根据这个东西来列不等式。
最后反过来思考,为什么本题会有和 ( t DAG) 有关的这种结论?我的想法是首先可以构造出一种 (2n-1) 的图使得任意两点之间都有路径,但是因为有些点对之间并不需要有路径所以这种构造不优,那么就可以联想到 ( t DAG) 中的点只需要有拓扑序小到大的路径,那么就可以在 ( t DAG) 上缩减边数。
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,ans,mx,fa[20],out[20],dp[1<<20];
char s[M],t[M];
int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
void work()
{
n=read();scanf("%s%s",s,t);ans=mx=0;
for(int i=0;i<20;i++) fa[i]=i,out[i]=0;
for(int i=0;i<(1<<20);i++) dp[i]=0;
for(int i=0;i<n;i++)
{
int x=s[i]-'a',y=t[i]-'a';
out[x]|=(1<<y);
fa[find(x)]=find(y);
}
ans=40;dp[0]=1;
for(int i=0;i<20;i++)
if(i==find(i)) ans--;
for(int i=0;i<(1<<20);i++) if(dp[i])
{
mx=max(mx,__builtin_popcount(i));
for(int j=0;j<20;j++)
if(!(i&(1<<j)) && (out[j]&i)==0)
dp[i|(1<<j)]=1;
}
printf("%d
",ans-mx);
}
signed main()
{
T=read();
while(T--) work();
}