向量的叉积
向量叉积的几何意义是两向量由平行四边形法则围成的面积(正弦定理),公式:
这个东西根据计算的结果可以说明一些东西,假设 (vec a,vec b) 向量共起点:
- 如果 (vec a imesvec b=0) 的话那么说明这两个向量贡献。
- 如果 (vec a imes vec b>0) 那么 (sin heta>0),也就是 (vec a) 到 (vec b) 的逆时针转角不超过 (180) 度,那么说明 (vec b) 的终点在 (vec a) 的左侧。
- 如果 (vec a imesvec b<0),那么说明 (vec b) 的终点在 (vec a) 的右侧。
线段交点
思路就是用叉积算面积比例去表示线段比例,然后用线段端点来计算交点,如下图:

设 (S_{Delta ACD}:S_{Delta BCD}=omega_1:omega_2),那么 ((x_o,y_o)=vec O=frac{omega_2vec A+omega_1vec B}{omega_1+omega_2}),就不需要麻烦地解方程了。
向量旋转
感觉就用高中数学知识推导一下就行了诶。
设 (vec a=(x,y)),倾角为 ( heta),长度为 (l=sqrt{x^2+y^2}),则 (x=lcos heta,y=lsin heta),假设其旋转 (alpha) 度角,得到向量 (vec b=(lcos( heta+alpha),lsin( heta+alpha))),然后把这个东西直接展开:
三角剖分
可以用三角剖分来求任意多边形的面积,也就是把多边形面积表示成三角形(有正负)。
我们把相邻两个顶点与原点构成向量叉积数值的一半累加起来,即可得到面积:
下面有白嫖过来的图
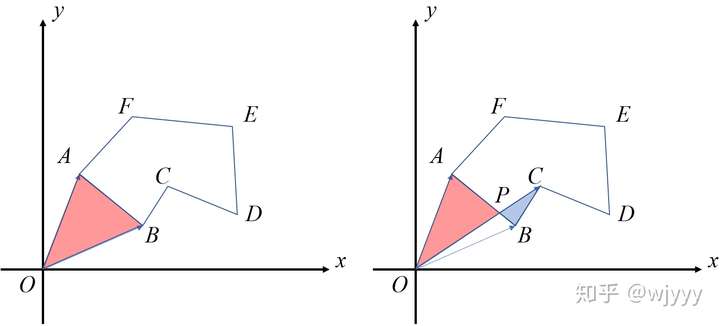
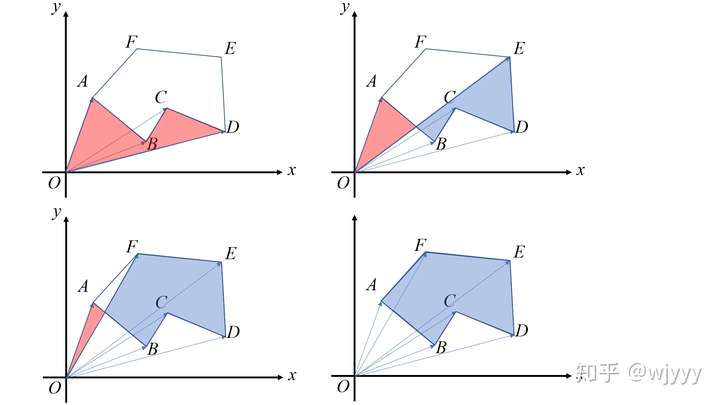
至于三角剖分为什么成立,这里引用知乎上的解释:
可以看出,多边形外部出现过的红色总会被消掉,因为多边形是闭合的。当出现了一条相对原点向右的边时,则之后必然会出现一条相对原点向左的边来封闭这个多边形。
如果原点在多边形内部就更好理解了。多边形凹的部分会被”拐回来的部分“给减掉,剩下的部分都可以直接相加。
线段相交
这个东西还是比较有意思的,我们先把线段相交分成严格相交和非严格相交。
所谓严格相交就是交点在线段的中心上,可以判断另一条线段的两个端点在这条线段的异侧。
非严格相交就先判断两个线段的 (x,y) 区间都相交,然后可以交在端点上,用叉积判断即可。
bool intersect(db l1,db r1,db l2,db r2)
{
if(l1>r1) swap(l1,r1);if(l2>r2) swap(l2,r2);
return !(cmp(r1,l2)==-1 || cmp(r2,l1)==-1);
//其中cmp就是比大小,r1<l2就返回-1
}
bool isSS(P p1,P p2,P q1,P q2)//传进去若干个向量
{
return intersect(p1.x,p2.x,q1.x,q2.x) && intersect(p1.y,p2.y,q1.y,q2.y) &&
crossop(p1,p2,q1)*crossop(p1,p2,q2)<=0 && crossop(q1,q2,p1)*crossop(q1,q2,p2)<=0;
//crossop就是用叉积判断向量在线段的哪一侧,必须在异侧或者是共线
}
旋转卡壳
这个算法用以求凸包的直径,先看几个定义吧:
如果一条直线和凸多边形有交点,并且整个凸多边形都在这条直线的一侧,就称该直线是凸多边形的切线。如果过凸多边形上两点作一对平行线,使得整个多边形都在这两条线之间,就称这两个点为一对对踵点。
可以证明直径一定在对踵点之间产生,因为如果不在可以通过平移到对踵点使得距离更大。而且对踵点满足构造平行线时距离最大,这个性质可以用来找对踵点。
如果我们想求凸包的直径,可以转化为找到每一个点的对踵点,尝试利用构造平行线距离最大这个性质,我们枚举一条边去找对应的对踵点,具体说来按逆时针顺序枚举边,指针维护对踵点 (j),对踵点的移动也是逆时针的,算他们之间的距离可以用叉积(除以向量的模长就是距离),找到之后更新答案即可。有一个嫖来的动图:
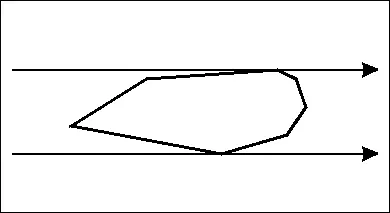
贴一个模板题的代码,注意点排序的时候一定要以 (x) 为第一关键字,(y) 为第二关键字排序。
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 100005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,tp,ans,st[M],use[M];
struct vec//向量结构体
{
int x,y;
vec(int X=0,int Y=0) : x(X) , y(Y) {}
vec operator - (vec b) {return vec(x-b.x,y-b.y);}
int operator * (vec b) {return x*b.y-b.x*y;}
int len() {return x*x+y*y;}//这道题不开方
bool operator < (const vec &b) const
{
if(x==b.x) return y<b.y;
return x<b.x;
}
}p[M],h[M];
int cross(vec a,vec b,vec c)//b,c平移到a的叉积
{
return (b-a)*(c-a);
}
signed main()
{
n=read();
for(int i=1;i<=n;i++)
p[i].x=read(),p[i].y=read();
sort(p+1,p+1+n);
st[++tp]=1;
for(int i=2;i<=n;i++)
{
while(tp>1 && (p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0)
use[st[tp--]]=0;
use[i]=1;
st[++tp]=i;
}
int tmp=tp;
for(int i=n;i>=1;i--)
if(!use[i])
{
while(tp>tmp && (p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0)
tp--;
st[++tp]=i;
}
//注意st[tp]的值也是1
for(int i=1;i<=tp;i++)
h[i]=p[st[i]];
int j=2;//对踵点,不要从1开始
ans=max(ans,(h[2]-h[1]).len());//判一下两个点
for(int i=1;i<tp;i++)
{
while(cross(h[i],h[i+1],h[j])<cross(h[i],h[i+1],h[j+1]))
j=j%(tp-1)+1;//直接比叉积
ans=max(ans,max((h[i]-h[j]).len(),(h[i+1]-h[j]).len()));
}
printf("%lld
",ans);
}
半平面交
所谓半平面交就是我们保留每条线段的左侧,求这些半平面的交集,可以应用于凸多边形面积交等问题中。
思路就是先把所有线段按极角排序,然后一个一个加入,取更新半平面交。
极角排序就是按与 (x) 轴正半轴的交角排序,用 (atan2) 这个函数即可,返回一个 ([-pi,pi]) 直接的角度。
那么怎么维护加入的这些线段呢?可以使用双端队列,具体原因要看图:
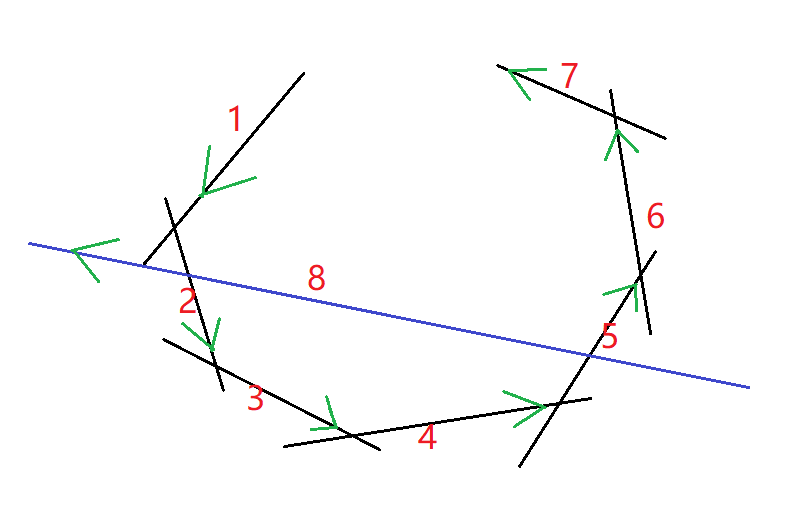
线段是按极角排序的所以可以构成换,当插入 (8) 这条线段的时候 (1,7,6) 这些线段都应该被废弃掉,所以我们使用的数据结构应该是支持在末尾插入和首尾弹出的,那就用双端队列呗。
那么考虑怎么样判断线段对半平面交有无影响,我们在双端队列中维护出线段的交点,看图:

不难发现如果交点在线段的右侧那么双端队列的线段就可以弹出了,首尾都弹一下即可。
计算交点就用上面讲的线段交点,但是可能会有线段平行的情况,那就没有交点,我们直接取最左边的线段即可,这个也可以用叉积判断一下。最后还要把首尾的交点计算出来。
求面积就用三角剖分即可,时间复杂度 (O(nlog n))
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
#define db double
const db eps = 1e-9;
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,st,en;db ans;
struct vec//向量
{
db x,y;
vec(db X=0,db Y=0) : x(X) , y(Y) {}
void get() {x=read();y=read();}
vec operator + (vec b) {return vec(x+b.x,y+b.y);}
vec operator - (vec b) {return vec(x-b.x,y-b.y);}
vec operator * (db b) {return vec(x*b,y*b);}
vec operator / (db b) {return vec(x/b,y/b);}
db operator * (vec b) {return x*b.y-b.x*y;}//叉积
}a[M],s[M];
struct line//线段
{
vec a,b;db k;
line() {}
line(vec A,vec B) : a(A) , b(B) {k=atan2(b.y,b.x);}
bool operator < (const line &r) const
{
return k<r.k;//极角排序
}
}p[M],t[M];
vec get(line a,line b)//求交点
{
vec A=a.a,B=a.a+a.b,C=b.a,D=b.a+b.b;
db w1=(D-A)*(C-A),w2=(C-B)*(D-B);
return (A*w2+B*w1)/(w1+w2);
}
void fuck()//半平面交
{
st=en=1;
t[st]=p[1];
for(int i=2;i<=n;i++)
{
while(st<en && p[i].b*(s[en-1]-p[i].a)<=eps) en--;
while(st<en && p[i].b*(s[st]-p[i].a)<=eps) st++;
t[++en]=p[i];
if(fabs(t[en].b*t[en-1].b)<=eps)//平行
{
en--;
if(t[en].b*(p[i].a-t[en].a)>eps)
t[en]=p[i];//取左边
}
if(st<en) s[en-1]=get(t[en-1],t[en]);
}
while(st<en && t[st].b*(s[en-1]-t[st].a)<=eps) en--;
if(en-st<=1) return ;
s[en]=get(t[st],t[en]);//求首尾的交点
}
signed main()
{
m=read();
for(int i=1;i<=m;i++)
{
k=read();a[1].get();
for(int j=2;j<=k;j++)
{
a[j].get();
p[++n]=line(a[j-1],a[j]-a[j-1]);
}
p[++n]=line(a[k],a[1]-a[k]);
}
sort(p+1,p+1+n);
fuck();
for(int i=st;i<=en;i++)
{
int j=(i==en)?st:i+1;
ans+=s[i]*s[j];
}
printf("%.3f",ans/2);
}