莫比乌斯反演---基础
前置芝士:
1.数论函数
:指定义域为正整数、陪域为复数的函数,每个算术函数都可视为复数的序列。
---来自百度百科
2.积性函数:
若f(x)为一个数论函数,且对于每一个互质的a,b满足
[f(a*b)=f(a)*f(b)
]
则f(x)为积性函数.
--完全积性函数:若f(x)为一个数论函数,且对于每一对a,b满足
[f(a*b)=f(a)*f(b)
]
则f(x)为完全积性函数.
例:积性函数有:
[\sigma_{k}(n)(表示n的所有约数的k次幂的和)
\
varphi(n)也为不超过n且与n互质的数的个数.
\
mu(n) = �egin{cases}
1&n=1 \
(-1)^k&n为k个不同质数的积\
0&else
end{cases}
]
完全积性函数有:
[幂函数 n^k\
单位函数epsilon(n)=�egin{cases}
1&n=1\
0&n>1
end{cases}
]
把积性函数与狄利克雷卷积(下面要学)联系起来,可以得到
若f,g为积性函数,则f*g也为积性函数.
[(f*g)(a imes b)=sumlimits_{d|ab}f(d)g(frac{ab}{d})\
令d=d_1 imes d_2\
=sumlimits_{d_1d_2|ab}f(d_1d_2)g(frac{ab}{d_1d_2})\
=sumlimits_{d_1|a}f(d_1)g(frac{a}{d_1}) imes sumlimits_{d_2|d}f(d_2)g(frac{b}{d_2})\
=(f*g)(a) imes (f*g)(b)
]
线性筛(实际上是利用线性筛求积性函数的值)
唯一分解定理:任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积
那么有
[mathbf{f}(n)=prodlimits_{i=1}^tmathbf{f}(p_i^{k_i})
]
于是我们就有另一种方法表示积性函数,即给出它在素数幂处的取值
当我们在线性筛的时候可以求出每个数的最小质因数(p_1),它的次数(k_1),那么
[mathbf{f}(n)=mathbf{f}(p_1^{k_1})mathbf{f}(frac{n}{p_1^{k_1}})
]
由上面的结论可知:
[sigma_0(n)=prodlimits_{i=1}^t(k_i+1)\
phi(n)=prodlimits_{i=1}^tp_i^{k_i-1}(p_i-1)=nprodlimits_{i=1}^t(1-frac{1}{p_i})
]
(下面的那个是不是有点熟悉?就是课本上欧拉函数的求法)
3.函数之间的加法和数乘
[(f+g)(n)=f(n)+g(n)
\加法\(x imes f)(n)=x imes f(n),xepsilon C\
(c为常数) 数乘
]
4.狄利克雷卷积(Dirichlet)
Dirichlet是个人,而且是一个很有名的人,今天我们不讲这个人,我们讲讲他的狄利克雷卷积
狄利克雷乘积(Dirichlet product)亦称狄利克雷卷积、卷积,是数论函数的重要运算之一。设f(n)、g(n)是两个数论函数,它们的Dirichlet(狄利克雷)乘积也是一个数论函数,简记为h(n)=f(n)*g(n)。---来自百度百科
[(f*g)=sumlimits_{ij=n}f(i)g(j)\或\(f*g)=sumlimits_{d|n}f(d)f(frac{n}{d})
]
运算性质:满足交换律,结合律,分配律;
交换律 即
[(f*g)=(f*g)\
]
[--------------\
证明:\(f*g)(n)=sumlimits_{ij=n}f(i)g(j)=sumlimits_{ji=n}f(j)g(i)=(g*f)(n)
]
结合律:
[(f*g)*h=f*(g*h)
]
[证明:\ [((f*g)*h)](n)=sumlimits_{pq=n}[sumlimits_{ij=p}f(i)g(j)]h(q)\
=sumlimits_{i|n}f(i)(sumlimits_{jq=frac{n}{i}}g(j)h(q))\
=sumlimits_{i|n}f(i)(g*h)(frac{n}{i})\
=(f*(g*h))(n)
]
分配律:
[f*(g+h)=f*g+f*h
]
[证明:\
f*(g+h)=[f*(g+h)](n)\
=sumlimits_{d|n}f(d) imes[g(frac{n}{d})+h(frac{n}{d})]\
=sumlimits_{d|n}[f(d)g(frac{n}{d})+f(d)h(frac{n}{d})]\
=f*g+f*h
]
单位元
在狄利克雷卷积中存在一种像单位矩阵一样的"数",任何一个函数*这个"数"都会是其本身,我们把这个"数"叫做单位元,即前文所提到的单位函数
[epsilon(n)=�egin{cases}1&n=1\
0&n>1\
end{cases}
]
则有
[(f*epsilon)(n)=sumlimits_{d|n,d
eq n}f(d)epsilon(frac{n}{d})+f(n)epsilon(1)\
=sumlimits_{d|n,d
eq n}f(d) imes0+1\]
=f(n)
]
所以任何一个数论函数与单位元的卷积为数论函数本身(后文有重要运用)
逆元
其实逆元的概念和倒数差不多,即:
方程 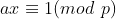 的解称为
的解称为  关于模
关于模 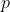 的逆,当
的逆,当 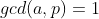 (即
(即  ,
,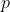 互质)时,方程有唯一解,否则无解。
互质)时,方程有唯一解,否则无解。
那么逆元可以用来干什么呢,比如说对于 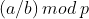 ,并没有
,并没有 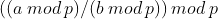 ,但是直接除又会爆精度,这时我们就可以用到逆元,假设用
,但是直接除又会爆精度,这时我们就可以用到逆元,假设用 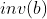 代表
代表 
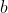 的逆元,那么
的逆元,那么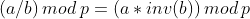 。 ____引用自forever_dreams的博客
。 ____引用自forever_dreams的博客
上面的是数的逆元,狄利克雷卷积也有逆元:
定义:
[对每个mathbf{f}(1)
eq 0的函数mathbf f ,都存在一个函数mathbf{g}使得mathbf{f}*mathbf{g}=epsilon
]
则如何求一个函数的逆?
定义
[mathbf{g}(n)=frac{1}{mathbf{f}(1)}left([n=1]-sumlimits_{ij=n,i
eq 1}mathbf{f}(i)mathbf{g}(j)
ight)
]
则
[mathbf{f}*mathbf{g}(n)\
=sumlimits_{ij=n}mathbf{f}(i)mathbf{g}(j)\
=mathbf{f}(1)mathbf{g}(n)+sumlimits_{ij=n,i
eq 1}mathbf{f}(i)mathbf{g}(j)\=[n=1]=epsilon(i)
]
把积性函数和逆元联系起来得到 积性函数的逆元一定也是积性函数.
留与读者自证之/笑哭.(注,积性函数一定满足 f ( 1 ) = 1 )
莫比乌斯反演
[我们定义1的逆是 mu.\
这样的话,如果g=f*1,就有f=f*1*mu=g*mu,\
换句话说,如果 mathbf g(n)=sum_{dmid n}mathbf f(d) \就有 mathbf f(n)=sum_{dmid n}muleft(frac nd
ight)mathbf g(d)
]
[引理
\mu*1=epsilon\
即 sumlimits_{d|n}mu(d)=epsilon(n)\其中的"1"是一个返回值为1的常数函数
]
证明:
[设n有k个不同的质因子
\n=p_1 imes p_2 imes ... imes p_k\
记一个函数q(s)为序列mathbf{s}中所有元素的乘积\
mathbf{s}={{x_1,x_2...x_k}};s序列长度为K
\令一个mathbf{f}(s)的约数d=mathbf{f}(j)
\jsubseteq s, j序列长度为J\
herefore sumlimits_{d|n}mu(d)=sumlimits_{mathbf{J}=0}^kmu(f(j)) imes (从K中取J个值(组合数))\
令i=J,则原式=sumlimits_{i=0}^kmu(d)^i(k中取i的组合)\
根据二项式定理,奇数项与偶数项和为0.
所以sumlimits_{d|n}mu(n) = �egin{cases}
1&n=1 \
0&n>1\
end{cases}=epsilon(n)
]
求解μ
[如何求mu ?由于1是积性的,所以1的逆mu也是积性的,则
]
[mu(p^k)�egin{cases}1,&k=0\-1,&k=1\0,&k>1end{cases}
]
[mu(x)=�egin{cases}
1,&x=1\
(-1)^n, &x=prodlimits_{i=1}^np_i\
0,&其余情况
end{cases}
]
[求mu的函数
]
void get_mu(int n)
{
mu[1] = 1;
for(int i = 2;i <= n; i++)
{
if(!vis[i])
{
pri[++cnt] = i;
mu[i] = -1;
}
for(int j = 1; j <= cnt && pri[j] * i <= n; j++)
{
vis[pri[j] * i] = 1;
if(i % pri[j] == 0) break;
else mu[i * pri[j]] = -mu[i];
}
}
}
这样就证明了上述结论。
当然还有另一个方向的莫比乌斯反演(这个大概更常用)
[mathbf{g}(n)=sumlimits_{n|d}mathbf{f}(d)iff mathbf{f}(n)=sumlimits_{n|d}mu(frac{d}{n})mathbf{g}(d)
]
[对此只需要定义 (mathbf foplusmathbf g)(x)=sum_{xmid y}mathbf f(y/x)mathbf g(y)=sumlimits_{x|Y}f(y/x)g(y) ,并容易证明 (mathbf fastmathbf g)oplusmathbf h=mathbf foplus(mathbf goplusmathbf h)。\于是
mathbf f=(muastmathbf1)oplusmathbf f=muoplus(mathbf1oplusmathbf f)=muoplusmathbf g
]
莫比乌斯反演是一个很重要的数论知识,在做数论题的时候很有帮助,为了提高对于莫比乌斯反演的理解和掌握
建议去看看以下几道题
YY的GCD
约数个数和
如果你看完了一遍,对于知识点还是没有理解的话,建议重新看一遍,或者去以下的博客那里看一看,
本人就是从那里学习的
铃悬的小知识
的解称为
关于模
的逆,当
(即
,
互质)时,方程有唯一解,否则无解。
,并没有
,但是直接除又会爆精度,这时我们就可以用到逆元,假设用
代表
的逆元,那么
。 ____引用自forever_dreams的博客