多项式全家桶

快速傅里叶变换

多项式的系数表示法

[f(x)=sum_{i=0}^{n-1}a_ix^i ]

即

[f(x) ightarrow {a_0,a_1,a_2dots ,a_{n-1}} ]

多项式的点值表示法

注意到一个最高次数为(n-1)的多项式可以由(n)个点值唯一确定
即将互不相同的({x_0,x_1,dots ,x_{n-1}})带入(f(x))得到(n)个取值({f(x_0),f(x_1),dots ,f(x_{n-1})})
因此

[f(x) ightarrow {f(x_0),f(x_1),dots ,f(x_{n-1})} ]

多项式乘法

注意到如果用系数表示法，直接做的复杂度为(mathcal O(n^2))（类似于高精度乘法）
但如果是点值表示法则可以做到(mathcal O(n))
即，对于两个多项式

[f(x) ightarrow {f(x_0),f(x_1),dots ,f(x_{n-1})}\ g(x) ightarrow {g(x_0),g(x_1),dots ,g(x_{n-1})} ]

那么

[h(x)=f(x)g(x) ightarrow {f(x_0)g(x_0),f(x_1)g(x_1),dots ,f(x_{n-1})g(x_{n-1})} ]

然而虽然理想美好，但是现实却很残酷
一般情况下都是用的系数表示法
于是自然而然地想到将系数表示法转化为点值表示法，乘出来之后再变回来
显然，暴力得到点值仍然是(mathcal O(n^2))的
于是我们考虑一些特殊的值带入

复数中的单位根

注意以下的(n)都是(2)的整数次幂
对于方程

[x^n=1 ]

由代数基本定理，这个方程应该存在(n)个根
不妨设这(n)个根为(w_n^0,w_n^1,dots ,w_n^{n-1})
容易发现

[w_n^k=cos(frac{2pi}nk)+icdot sin(frac{2pi}nk) ]

可以结合复平面上的单位圆进行理解
然后单位根有如下神奇性质

[w_n^a=w_{2n}^{2a}\ w_n^a=-w_n^{a+frac n2}\ w_n^a=w_n^{a-n} ]

然后就可以开始搞事情了

进入正题

注意以下的(n)都是(2)的整数次幂
不妨设

[f(x)=a_0+a_1x+a_2x^2dots +a_{n-1}x^{n-1}\ A(x)=a_0+a_2x+a_4x^2dots +a_{n-2}x^{frac{n-2}2}\ B(x)=a_1+a_3x+a_5x^2dots +a_{n-1}x^{frac{n-2}2} ]

即按照奇偶性分类
那么我们有

[f(x)=A(x^2)+xcdot B(x^2) ]

然后可以注意到

[f(w_n^k)=A(w_n^{2k})+w_n^kcdot B(w_n^{2k})\ =A(w_{frac n2}^k)+w_n^kcdot B(w_{frac n2}^k) ]

而

[f(w_n^{k+frac n2})=A(w_n^{2k+n})+w_n^{k+frac n2}cdot B(w_n^{2k+n})\ =A(w_n^{2k})+w_n^{k+frac n2}cdot B(w_n^{2k})\ =A(w_{frac n2}^k)-w_n^kcdot B(w_{frac n2}^k) ]

于是我们在计算(f(w_n^k))时就可以顺便计算出(f(w_n^{k+frac n2}))的值

这样就可以把(mathcal O(n^2))优化到(mathcal O(nlog_2n))

现在的问题就在于如何把点值再变回系数

考虑我们现在已经求出(h(x)=f(x)*g(x))在(w_n^0,w_n^1,dots w_n^{n-1})处的点值，需要求出(h(x))的各项系数(b_i)

考虑如此构造函数

[C(x)=sum_{i=0}^{n-1}h(w_n^i)x^i ]

那么

[C(x)=sum_{i=0}^{n-1}sum_{j=0}^{n-1}b_j(w_n^i)^jx^i ]

考虑将(x=w_n^{-0},w_n^{-1},dots w_n^{-(n-1)})带入(C(x))

[C(w_n^{-k})=sum_{i=0}^{n-1}sum_{j=0}^{n-1}b_j(w_n^i)^j(w_n^{-k})^i\ =sum_{i=0}^{n-1}sum_{j=0}^{n-1}b_j(w_n^{j-k})^i\ =sum_{j=0}^{n-1}b_jsum_{i=0}^{n-1}(w_n^{j-k})^i ]

考虑单位根反演定理

[[n|k]=frac 1nsum_{i=0}^{n-1}(w_n^k)^i ]

考虑证明此结论

当(nmid k)时，显然(w_n^k=1),因此原式(=frac 1nsum_{i=0}^{n-1}1^i=1)

当(n mid k)时，原式(=frac 1ncdot frac{(w_n^k)^n-1}{w_n^k-1}=frac 1ncdot frac{w_n^{kn}-1}{w_n^k-1}=frac 1ncdot frac{1-1}{w_n^k-1}=0)

因此

[C(w_n^{-k})=sum_{j=0}^{n-1}b_jn[nmid j-k]=nb_k ]

所以我们只用求出(C(x))在(x=w_n^{-0},w_n^{-1},dots w_n^{-(n-1)})的所有点值，最后再(/n)，就可以计算出(h(x))的各项系数了

于是我们就在(mathcal O(nlog_2n))的时间内完成了多项式乘法

但是倘若直接按照这样递归模拟，常数极大

我们考虑进行优化，直接把每个数交换到对应的位置上

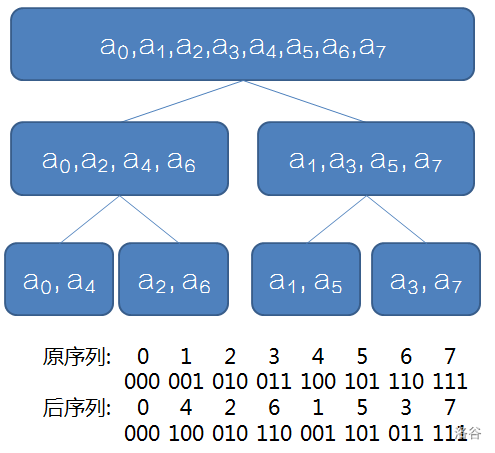
可以发现：交换后序列的位置为 交换前序列的二进制下 翻转过来

可以通过如下代码进行实现

for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));

在函数中这样实现

for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);

这样就可以化递归为迭代，大大减小常数

还有其他优化：比如预处理单位根。比较trivial就不再赘述了

完整代码

inline void fft(pt*p,int lim,int tp)
{
	for(int i=0;i<lim;++i)if(i<rev[i])swap(p[i],p[rev[i]]);
	for(int mid=1;mid<lim;mid<<=1)
	{
		pt w=pt(1.0,0.0),wn=pt(cos(pi/mid),1.0*tp*sin(pi/mid));
		for(int len=mid<<1,j=0;j<lim;j+=len,w=pt(1.0,0.0))
			for(int k=0;k<mid;++k,w=w*wn)
			{
				pt x=p[j+k],y=w*p[j+mid+k];
				p[j+k]=x+y,p[j+mid+k]=x-y;
			}
	}
}

其中(tp=1)表示为快速傅里叶变换，(tp=-1)表示快速傅里叶逆变换

快速数论变换

存在意义

普通的(FFT)显然无法支持取模操作

同时由于运用浮点数进行运算，包括大量使用如(sin,cos)这些函数，精度难免有误差

于是快速数论变换应运而生

阶

若 (a,p)互素，且 (p>1)，

对于 (a^n≡1(mod p))最小的 (n)，我们称之为 (a)模 (p)的阶,记做 (δ_p(a))

例如： (δ_7(2)=3)

原根

设 (p)是正整数，(a)是整数，若 (δ_p(a))等于(varphi (p))，则称 (a)为模 (p)的一个原根，记为 (g)

(δ_7(3)=6=varphi (7))，因此(3)模(7)的一个原根

注意原根的个数是不唯一的

原根有一个极其重要的性质

若(P)为素数，假设一个数(g)是(P)的原根，那么(g^i pmod P (0<i<P))的结果两两不同

进入正题

下证

[w_n^kequiv(g^{frac {p-1}n})^kpmod p ]

考虑单位根的所有性质

• (w_n^k=w_{2n}^{2k})

  (Leftrightarrow (g^{frac {p-1}n})^kequiv (g^{frac {p-1}{2n}})^{2k}pmod p)显然成立

• (w_n^k=-w_n^{k+frac n2})

  (Leftrightarrow (g^{frac {p-1}n})^kequiv -(g^{frac {p-1}n})^{k+frac n2})

  (Leftrightarrow g^{frac {p-1}{2}}equiv -1)

• (w_n^k=w_n^{k-n})

  (Leftrightarrow (g^{frac {p-1}n})^kequiv (g^{frac {p-1}n})^{k-n})

  (Leftrightarrow g^{p-1}equiv 1)

因此我们就可以用原根来替换单位根

常用的模数有(998244353,1004535809,469762049)，它们的原根都是(3)

其他地方都和(FFT)一模一样

代码如下

inline void ntt(int lim,poly&f,bool tp)
{
	for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
	for(int mid=1;mid<lim;mid<<=1)
	{
		int sw=qpow(tp?ivG:G,(mod-1)/(mid<<1));
		wn[0]=1;for(int i=1;i<mid;++i)wn[i]=mll(wn[i-1],sw);
		for(int len=mid<<1,p=0;p+len-1<lim;p+=len)
			for(int k=0;k<mid;++k)
			{
				int x=f[p+k],y=1ll*wn[k]*f[p+mid+k]%mod;
				f[p+k]=add(x,y),f[p+mid+k]=dec(x,y);
			}
	}
}

多项式求逆

给出(n-1)次函数(f(x))，求函数(g(x))满足

[g(x)equivfrac 1{f(x)}pmod {x^n} ]

系数均对(998244353)取模

考虑倍增法

不妨设我们已经求得函数(g_0)满足

[g_0cdot fequiv 1pmod {x^{frac n2}} ]

又由于

[gcdot fequiv 1pmod {x^{frac n2}} ]

所以

[fcdot (g-g_0)equiv 0pmod {x^{frac n2}}\ g-g_0equiv 0pmod {x^{frac n2}}\ (g-g_0)^2equiv 0pmod {x^{n}}\ g^2-2gcdot g_0+g_0^2equiv 0pmod {x^{n}}\ fcdot (g^2-2gcdot g_0+g_0^2)equiv 0pmod {x^{n}}\ g-2g_0+fcdot g_0^2equiv 0pmod {x^{n}}\ gequiv 2g_0-fcdot g_0^2pmod {x^{n}}\ ]

特别地，当(f(x)=c)时，(g(x)=c^{p-1})

然后递归求解即可

注意此处常数的优化

poly ginv(int n,poly f)
{
	if(n==1){poly g;g[0]=qpow(f[0],mod-2);return g;}
	poly g=ginv(n+1>>1,f),h,p=g;
	int lim=1,l=0;while(lim<n+n)lim<<=1,++l;
	for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
	f.pre(n,lim),p.pre(n,lim);
	ntt(lim,f,0),ntt(lim,p,0);
	for(int i=0;i<lim;++i)f[i]=mll(f[i],mll(p[i],p[i]));
	ntt(lim,f,1);int iv=qpow(lim,mod-2);
	for(int i=0;i<n;++i)h[i]=dec(add(g[i],g[i]),mll(f[i],iv));
	return h;
}

多项式( ext{ln})

给出(n-1)次的多项式函数(f(x)),求函数(g(x))满足

[g(x)equivln f(x)pmod {x^n} ]

系数均对(998244353)取模,保证(f(0)=1)

两边同时求导可以得到

[g'equiv(ln f)'pmod {x^n}\ g'equivfrac {f'}fpmod {x^n}\ gequiv int frac {f'}fpmod {x^n} ]

于是多项式求逆+多项式求导+多项式积分即可

来康康具体实现

inline void igl(int n,poly&f)
{
	for(int i=n-1;i;--i)f[i]=mll(f[i-1],inv[i]);f[0]=0;
}//积分
inline void diff(int n,poly&f)
{
	for(int i=0,t=f[i+1];i<n-1;++i,t=f[i+1])f[i]=mll(t,i+1);f[n-1]=0;
}//微分
inline poly ln(int n,poly f)
{
	poly g=ginv(n,f),h;diff(n,f);
	h=mul(n,n,g,f);igl(n,h);
	return h;
}

多项式牛顿迭代

对于函数方程

[F(G(x))equiv 0pmod {x^n} ]

已知(F(x))，求(G(x))

类似于倍增法

假设我们已经求出(G_0(x))满足

[F(G_0(x))equiv 0pmod {x^{frac n2}} ]

考虑在(G_0(x))处使用泰勒展开

[F(G(x))=sum_{i=0}^{+infty}frac{F^{(i)}(G_0(x))}{i!}(G(x)-G_0(x))^i ]

其中(f^{(i)})表示对(f)求(i)阶导

注意这个地方是把(G(x))当做自变量,(G_0(x))当作常数，因此不用考虑链式法则等因素

容易知道

[G(x)-G_0(x)equiv 0pmod {x^{frac n2}} ]

因此对于(forall ige2)

[(G(x)-G_0(x))^iequiv 0pmod {x^n} ]

所以

[F(G(x))equiv F(G_0(x))+F'(G_0(x))(G(x)-G_0(x))pmod {x^n}\ Leftrightarrow F(G_0(x))+F'(G_0(x))G(x)-F'(G_0(x))G_0(x)equiv 0pmod {x^n}\ Leftrightarrow G(x)equiv G_0(x)-frac{F(G_0(x))}{F'(G_0(x))}pmod {x^n} ]

于是这样不断迭代下去即可求出答案

但要注意当(n=1)时需要特殊处理（即递归边界）

那这个东西有什么用呢？以下举两个例子

多项式(exp)

给出(n-1)次多项式(f(x))，求(g(x))满足

[g(x)equiv e^{f(x)}pmod {x^n} ]

系数均对(998244353)取模，保证(f(0)=0)

化一下柿子

[ln g(x)equiv f(x)pmod {x^n}\ Leftrightarrow ln g(x)-f(x)equiv 0pmod {x^n} ]

带入先前的牛顿迭代表达式可得

[g(x)equiv g_0(x)-frac{ln g_0(x)-f(x)}{frac 1{g_0(x)}}pmod {x^n}\ g(x)equiv g_0(x)(1-ln g_0(x)+f(x))pmod {x^n}\ ]

迭代即可

递归边界(g(x)equiv 1pmod x),因为题目保证函数(f(x))的常数项为(0)

代码如下

poly exp(int n,poly f)
{
	if(n==1){poly g;g[0]=1;return g;}
	poly g=exp(n+1>>1,f),h=ln(n,g);
	for(int i=0;i<n;++i)h[i]=add(dec(0,h[i]),f[i]);
    h[0]=add(h[0],1);
	return mul(n,n,g,h);
}

多项式开根

给出(n-1)次多项式(f(x))，求(g(x))满足

[g(x)equiv sqrt{f(x)}pmod {x^n} ]

系数均对(998244353)取模

仍然推柿子

[g^2(x)equiv f(x)pmod {x^n}\ g^2(x)-f(x)equiv 0pmod {x^n} ]

还是带入牛顿迭代表达式可得

[g(x)equiv g_0(x)-frac{g_0^2(x)-f(x)}{2g_0(x)}pmod {x^n} ]

多项式乘法+多项式求逆即可

递归边界(g(x)equivsqrt {f(0)} pmod {998244353})

于是求出(f(x))常数项的二次剩余即可

代码如下

inline poly sqr(int n,poly f)
{
	if(n==1){poly g;g[0]=solve(f[0]);return g;}
	poly g=sqr(n+1>>1,f),h,ivg;
	ivg=ginv(n,g),h=mul(n,n,g,g);
	int iv=qpow(2,mod-2);
	for(int i=0;i<n;++i)ivg[i]=mll(iv,ivg[i]);
	for(int i=0;i<n;++i)h[i]=dec(h[i],f[i]);
	h=mul(n,n,h,ivg);
	for(int i=0;i<n;++i)h[i]=dec(g[i],h[i]);
	return h;
}

多项式除法+取模

这个稍微trivial一点

给出(n-1)次多项式(f(x))和(m-1)次多项式(g(x))，求(q(x),r(x))满足

[f(x)=q(x)g(x)+r(x) ]

要求(r(x))的次数小于(m-1)
系数均对(998244353)取模
对于多项式

[F(x)=sum_{i=0}^{n-1}a_ix^i ]

我们定义

[F_R(x)=sum_{i=0}^{n-1}a_{n-i-1}x^i ]

形象地说，将(F(x))的系数倒过来
回到正题

[ecause f(x)=q(x)g(x)+r(x)\ herefore f(frac 1x)=q(frac 1x)g(frac 1x)+r(frac 1x)\ herefore x^{n-1}f(frac 1x)=x^{n-1}q(frac 1x)g(frac 1x)+x^{n-1}r(frac 1x)\ herefore x^{n-1}f(frac 1x)=x^{n-m}q(frac 1x)x^{m-1}g(frac 1x)+x^{n-m+1}cdot x^{m-2}r(frac 1x)\ herefore f_R(x)=q_R(x)g_R(x)+x^{n-m+1}r_R(x)\ herefore f_R(x)equiv q_R(x)g_R(x)pmod {x^{n-m+1}}\ herefore q_R(x)equiv frac{f_R(x)}{g_R(x)}pmod {x^{n-m+1}} ]

于是多项式求逆+乘法就可以求出(q(x))

那么

[r(x)=f(x)-q(x)g(x) ]

问题得以解决

求(q(x))代码如下

inline poly div(int n,int m,poly f,poly g)
{
	rv(n,f),rv(m,g);
	g=ginv(n-m+1,g);
	poly q=mul(n-m+1,n-m+1,f,g);
	rv(n-m+1,q);return q;
}

多项式快速幂（普通版）

给定(n-1)次多项式(f(x))和正整数(k),求(g(x))满足

[g(x)equiv f^k(x)pmod {x^n} ]

系数均对(998244353)取模且保证(f(0)=1)

首先对于多项式函数(f(x))满足(f(0)=1)证明如下命题：

[f^p(x)equiv 1pmod {x^n} ]

其中(p)是质数并且(n<p)

原命题等价于

[(1+sum_{i=1}^{n-1}a_ix^i)^pequiv 1pmod {x^n}\ Leftrightarrow 1^p+sum_{i=1}^{n-1}a_i^px^{ip}equiv 1pmod {x^n}\ Leftrightarrow 1equiv 1pmod {x^n}\ ]

其中第一步到第二步的变换可以由多项式定理来证明

于是

[g(x)equiv f^k(x)equiv f^{k\%p}(x)pmod {x^n} ]

不妨令(k'=k\%p)

先两边同时求(ln)

[ln g(x)equiv ln f^{k'}(x)equiv k'ln f(x)pmod {x^n} ]

再两边同时求(exp)

[g(x)equiv e^{k'ln f(x)}pmod {x^n} ]

于是就做完了

多项式快速幂（加强版）

同上，唯一区别在于不保证(f(0)=1)

这样会有什么影响呢?

回头一看发现如果不保证这一点那么(ln,exp)都没有办法做

于是考虑转化

我们需要找到(f)中最低的系数非零的项，记为(a_tx^t)，然后整个多项式除以(a_tx^t)，于是我们成功的让(a_0)变成了(1)，计算之后我们需要将答案右移(t^k)位，再乘(a_t^k)

但是还是有很多坑

• (t^k)如果大于等于(n)需要特判
• (t^k,a_t^k)中的(k)都应该对(mod-1)取模而不是(mod)

代码

inline poly fsp(int n,int k1,int k2,poly f)
{
	int u,k;poly ans;
	for(u=0;u<n&&!f[u];++u);k=qpow(f[u],k2);
	if(1ll*u*k2>=n)return ans;
	int iv=qpow(f[u],mod-2);
	for(int i=u;i<n;++i)f[i]=mll(f[i],iv);
	for(int i=0,j=u;j<n;++i,++j)ans[i]=f[j];
	ans=ln(n,ans);
	for(int i=0;i<n;++i)ans[i]=mll(ans[i],k1);
	ans=exp(n,ans);
	for(int i=0;i<u*k2;++i)f[i]=0;
	for(int i=u*k2,j=0;i<n;++i,++j)f[i]=mll(ans[j],k);
	return f;
}
int main()
{
	int n,k1=0,k2=0,k3=0;scanf("%d",&n);pre(n);
	scanf("%s",ch+1);int len=strlen(ch+1);
	poly f;read(n,f);
	for(int i=1;i<=len;++i)
	{
		k1=add(mll(10,k1),ch[i]^48),
		k2=(10ll*k2%(mod-1)+(ch[i]^48))%(mod-1);
		if(k1>n&&!f[0])//这里要特判
		{
			for(int i=0;i<n;++i)printf("0 ");
			return 0;
		}
	}
	print(n,fsp(n,k1,k2,f));
	return 0;
}

封装后所有的完整代码

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353,G=3,ivG=332748118,N=4e6+5;
inline int in()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return x*f;
} 
struct poly
{
	vector<int>v;
	inline int&operator[](int x)
	{
		while(x>=v.size())v.push_back(0);
		return v[x];
	}
	inline void pre(int x,int lim)
	{
		int t=min(lim,(int)v.size());
		for(int i=x;i<t;++i)v[i]=0;
	}
};
namespace Math
{
	int inv[N],pif;
	inline int add(int x,int y){x+=y;return x>=mod?x-mod:x;}
	inline int dec(int x,int y){x-=y;return x<0?x+mod:x;}
	inline int mll(int x,int y){return 1ll*x*y%mod;}
	struct pt
	{
		int x,y;
		pt(int _x=0,int _y=0){x=_x,y=_y;}
		inline pt operator*(const pt&rhs)
		{
			return pt(add(mll(x,rhs.x),mll(mll(y,rhs.y),pif)),add(mll(x,rhs.y),mll(y,rhs.x)));
		}
	};
	inline int qpow(int x,int y)
	{
		int ans=1;
		for(;y;y>>=1,x=mll(x,x))(y&1)&&(ans=mll(ans,x));
		return ans;
	}
	inline pt qpow(pt x,int y)
	{
		pt ans=pt(1,0);
		for(;y;y>>=1,x=x*x)if(y&1)ans=ans*x;
		return ans;
	}
	inline void pre(int n)
	{
		inv[1]=1;
		for(int i=2;i<=n;++i)inv[i]=mod-mll(mod/i,inv[mod%i]);
	}
	inline bool ck(int x){return qpow(x,(mod-1)>>1)==mod-1;}
	inline int solve(int x)
	{
		int ans=0;
		if(mod==2)return x;
		if(!x)return 0;
		else if(qpow(x,(mod-1)>>1)==mod-1)return -1;
		int a=rand()%mod;
		while(!a||!ck(dec(mll(a,a),x)))a=rand()%mod;
		pif=dec(mll(a,a),x);
		ans=qpow(pt(a,1),(mod+1)>>1).x;
		return min(ans,mod-ans);
	}//二次剩余求解
}
using namespace Math;
namespace Bas
{
	int rev[N],wn[N];
	inline void ntt(int lim,poly&f,bool tp)
	{
		for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
		for(int mid=1;mid<lim;mid<<=1)
		{
			int sw=qpow(tp?ivG:G,(mod-1)/(mid<<1));
			wn[0]=1;for(int i=1;i<mid;++i)wn[i]=mll(wn[i-1],sw);
			for(int len=mid<<1,p=0;p+len-1<lim;p+=len)
				for(int k=0;k<mid;++k)
				{
					int x=f[p+k],y=1ll*wn[k]*f[p+mid+k]%mod;
					f[p+k]=add(x,y),f[p+mid+k]=dec(x,y);
				}
		}
	}
	inline poly mul(int n,int m,poly f,poly g)
	{
		int lim=1,l=0;while(lim<n+m)lim<<=1,++l;
		for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
		f.pre(n,lim),g.pre(m,lim);
		ntt(lim,f,0),ntt(lim,g,0);
		for(int i=0;i<lim;++i)f[i]=mll(f[i],g[i]);
		ntt(lim,f,1);int iv=qpow(lim,mod-2);
		for(int i=0;i<lim;++i)f[i]=mll(f[i],iv);
		return f;
	}//乘法
	inline void igl(int n,poly&f)
	{
		for(int i=n-1;i;--i)f[i]=mll(f[i-1],inv[i]);f[0]=0;
	}//积分
	inline void diff(int n,poly&f)
	{
		for(int i=0,t=f[i+1];i<n-1;++i,t=f[i+1])f[i]=mll(t,i+1);f[n-1]=0;
	}//微分（注意这里写得不当很容易RE）
	inline void rv(int n,poly&f){reverse(f.v.begin(),f.v.begin()+n);}
	inline void read(int n,poly&f){for(int i=0;i<n;++i)f[i]=in();}
	inline void print(int n,poly f){for(int i=0;i<n;++i)printf("%d ",f[i]);puts("");}
}
using namespace Bas;
namespace Poly
{
	poly ginv(int n,poly f)
	{
		if(n==1){poly g;g[0]=qpow(f[0],mod-2);return g;}
		poly g=ginv(n+1>>1,f),h,p=g;
		int lim=1,l=0;while(lim<n+n)lim<<=1,++l;
		for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
		f.pre(n,lim),p.pre(n,lim);
		ntt(lim,f,0),ntt(lim,p,0);
		for(int i=0;i<lim;++i)f[i]=mll(f[i],mll(p[i],p[i]));
		ntt(lim,f,1);int iv=qpow(lim,mod-2);
		for(int i=0;i<n;++i)h[i]=dec(add(g[i],g[i]),mll(f[i],iv));
		return h;
	}//多项式求逆
	inline poly ln(int n,poly f)
	{
		poly g=ginv(n,f),h;diff(n,f);
		h=mul(n,n,f,g);igl(n,h);
		return h;
	}//多项式求ln
	poly exp(int n,poly f)
	{
		if(n==1){poly g;g[0]=1;return g;}
		poly g=exp(n+1>>1,f);
		poly h=ln(n,g);
		for(int i=0;i<n;++i)h[i]=add(dec(0,h[i]),f[i]);
        h[0]=add(h[0],1);
		return mul(n,n,g,h);
	}//多项式求exp
	inline poly div(int n,int m,poly f,poly g)
	{
		rv(n,f),rv(m,g);
		g=ginv(n-m+1,g);
		poly q=mul(n,n-m+1,f,g);
		rv(n-m+1,q);return q;
	}//多项式除法求商式
	inline poly sqr(int n,poly f)
	{
		if(n==1){poly g;g[0]=solve(f[0]);return g;}
		poly g=sqr(n+1>>1,f),h,ivg;
		ivg=ginv(n,g),h=mul(n,n,g,g);
		int iv=qpow(2,mod-2);
		for(int i=0;i<n;++i)ivg[i]=mll(iv,ivg[i]);
		for(int i=0;i<n;++i)h[i]=dec(h[i],f[i]);
		h=mul(n,n,h,ivg);
		for(int i=0;i<n;++i)h[i]=dec(g[i],h[i]);
		return h;
	}//多项式开根
	inline poly fsp(int n,int k1,int k2,poly f)
	{
		int u,k;poly ans;
		for(u=0;u<n&&!f[u];++u);k=qpow(f[u],k2);
		if(1ll*u*k2>=n)return ans;
		int iv=qpow(f[u],mod-2);
		for(int i=u;i<n;++i)f[i]=mll(f[i],iv);
		for(int i=0,j=u;j<n;++i,++j)ans[i]=f[j];
		ans=ln(n,ans);
		for(int i=0;i<n;++i)ans[i]=mll(ans[i],k1);
		ans=exp(n,ans);
		for(int i=0;i<u*k2;++i)f[i]=0;
		for(int i=u*k2,j=0;i<n;++i,++j)f[i]=mll(ans[j],k);
		return f;
	}//多项式快速幂
}
using namespace Poly;
char ch[N];
int main(){return 0;}
//上面所有的n都表示n-1次多项式