本文接排序算法总结一
3. 冒泡排序
冒泡排序的基本思想:以正序排列为例,我们首先要将最大的数沉到最底下,从第一个数开始,比较相邻的两个数,如果为逆序则交换这两个数,重复这个操作直到倒数第二个数,此时最大的数已沉到最底下;然后再从第一个数开始,用同样的方法将次大的数沉到次底下,重复这个过程直到排序成功。代码如下:
void PaoSort1(vector<int>& a) { int length = a.size(); for (int i = 0; i < length - 1; i++) { for (int j = 0; j < length -1-i; j++) { if (a[j]>a[j+1]) Swap(a[j], a[j+1]); } } }
注意上面的内循环j的判断条件,每当外部循环i加1表示,底部多了一个数,所以j跳出条件为length-1-i,这个过程其实是泡沫沉底。而真正的冒泡是从底部向上升,这个过程与沉底类似,只不过内部循环中的j从最后一个数开始,每次循环后j值递减,而循环跳出条件为j<i.
上述代码的缺点是当序列已经有序了,而循环没有结束,会继续进行比较操作,这样便增加了运行时间。为了提高速度我们可以设置一个标记来查看是否进行了交换,并把这个标签加入到外部循环的判断条件,这样如果没有交换说明已经排序完成,程序返回。代码如下:
void Paosort2(vector<int>& a) { int length = a.size(); bool flag = true; for (int i = 0; flag&&i < length - 1; i++) { flag = false; for (int j = 0; j < length -1-i; j++) { if (a[j]>a[j + 1]) { Swap(a[j], a[j+1]); flag = true; } } } }
选择排序可以通过一次选出最大值与最小值来提高速度,冒泡排序也可以采用同样的方法,即同时向上和向下进行冒泡,代码如下:
void Mymath::Paosort3(vector<int>& a) { int length = a.size(); bool flag = true; for (int i = 0; flag&&i <= length / 2; i++) { flag = false; for (int j = length - 2; j >=i; j--) { if (a[j]>a[j + 1]) { Swap(a[j], a[j+1]); flag = true; } if (a[length - 2 - j]>a[length - 2- j]) { Swap(a[length - 1 - j], a[length - j]); flag = true; } } } }
时间复杂度:如果序列是正序的,则只需要进行n-1次比较,不用交换,此时的时间复杂度为O(n),当为逆序时,比较次数为1+2+...+n-1=n(n-1)/2,交换次数与此相同,时间复杂度为O(n^2),该算法是稳定的。
4. 归并排序
归并排序的基本思想:将含有n个记录的序列看成n个包含1个记录的子序列,将子序列两两合并,得到n/2(向上取整)个2个记录或一个记录的序列,如此重复此过程最终构成一个包含n个记录的有序序列,这种方法叫2路归并排序,这里只介绍这种方法。
在进行合并之前,我们先要将原序列切分为n个子序列,可以采用二分的方法,每次将原有的每个序列分为两个,这里采用递归的方法直到所有的序列的长度都为1后开始进行合并,具体代码如下:
1 void Msort(int a[], int first, int last, int temp[]) 2 { 3 if (first < last) 4 { 5 int mid = (first + last) / 2; 6 Msort(a, first, mid, temp); //左边有序 7 Msort(a, mid + 1, last, temp); //右边有序 8 Merge(a, first, mid, last, temp); //再将二个有序数列合并 9 } 10 }
Merge函数就是将两个有序序列合并为一个有序序列(最初的时候每个序列只有一个元素自然是有序的),其中的temp参数起到中间变量的作用,先将归并后的结果保存到temp中,归并结束后再将其中的值重新赋给a,然后将其释放,Merge函数的代码如下:
1 void Merge(int a[], int first, int mid, int last, int temp[]) 2 { 3 int i = first, j = mid + 1; 4 int m = mid, n = last; 5 int k = 0; 6 7 while (i <= m && j <= n) 8 { 9 if (a[i] <= a[j]) 10 temp[k++] = a[i++]; 11 else 12 temp[k++] = a[j++]; 13 } 14 15 while (i <= m) 16 temp[k++] = a[i++]; 17 18 while (j <= n) 19 temp[k++] = a[j++]; 20 21 for (i = 0; i < k; i++) 22 a[first + i] = temp[i]; 23 }
最后给出归并排序的整个代码:
1 void MergeSort(int a[], int n) 2 { 3 int *p = new int[n]; 4 Msort(a, 0, n - 1, p); 5 delete[] p; 6 }
时间复杂度:Msort函数中的将一个长度为n的序列切用二分法将其分为n个长度为1的子序列,这个时间复杂度为O(logn),而Merge函数中的时间复杂度为O(max(m,n)),所以整个过程的时间复杂度为O(nlog n). 空间复杂度:Msort函数递归了logn次,加上使用一个大小为n的变量作中间值,所以空间复杂度为O(n+log n).
5. 快速排序
快速排序的基本思想:在给出的序列中找一个数作为哨兵,我们以第一个数为例,将序列中比它大的元素排在它的后面,将比它小的元素排到它的前面,这是一次排序的结果,然后对哨兵前后的两个序列采用同样的方法进行排序,直到成为一个有序的序列。我们下面先看一次排序的代码:
1 int Partition(int* a, int p,int r) 2 { 3 int elem=a[p]; 4 int i=r; 5 for(int j=r;j>p;j--) 6 { 7 if(a[j]>elem) 8 { 9 Swap(a[i],a[j]); 10 i--; 11 } 12 } 13 Swap(a[i],a[p]); 14 return i; 15 }
例如序列为49,38,65,97,76,13,我们以第一个元素49为哨兵,用i指向尾端(第四行代码),我们要从尾端开始,将大于哨兵的数移动到尾端,首先比较尾端数据13和哨兵,比哨兵小则什么也不做,i依然指向尾端,进入下一次循环,76比哨兵大,所以将其与i所指数交换,即将其移动到尾端,然后i向前移动一位,此时序列为49,38,65,97,13,76, i指向13,下一个循环97比哨兵大,将其与i所指数交换,i向前移动一位,此时序列为49,38,65,13,97,76 ,i指向13,下一个循环后序列为49,38,13,65,97,76 ,i指向13,下一个循环j指向38,它比哨兵小,什么都不做,下一个循环j=p,不满足循环条件,此时循环退出。然后交换a[p]与a[i](第13行代码),序列为13,38,49,65,97,76,此时a[i]中的数等于哨兵,前面的数都小于它,而后面的数大于它,完成一次排序。
有的书上使用的两个指针的方法来实现一次排序,代码如下:
1 int Partition1(int* a, int p, int r) 2 { 3 int elem = a[p]; 4 while (p < r) 5 { 6 while (p < r && a[r] >= elem) 7 r--; 8 a[p] = a[r]; 9 while (p < r && a[p] <= elem) 10 p++; 11 a[r] = a[p]; 12 } 13 a[p] = elem; 14 return p; 15 }
此方法将第一个位置作为哨兵,并将其作为第一个将被填的坑,先从后向前找一个比哨兵小的元素,然后将其填入坑中,即哨兵位置,此时该元素的位置成为第二个坑;从前向后找一个比哨兵大的元素,将其填入坑中,该元素位置成为下一个坑;然后又从后向前找,以此循环直到前后两个指针相等为止,此时将哨兵填入最后的坑中(第13行代码),排序结束。
一次排序后,将哨兵前面的序列和后面的序列采用同样的方法继续进行排序,直到序列中的元素个数为一,即上述代码中的p 和 r相等,则结束,整个序列已成为一个有序的序列,代码如下:
1 void QuickSort(int a[],int p,int r) 2 { 3 int q; 4 if (p<r) 5 { 6 srand((unsigned)time(NULL)); //随机化算法 7 q=rand()%(r+1-p)+p; 8 Swap(a[p],a[q]); 9 q=Partition(a,p,r); 10 QuickSort(a,p,q-1); 11 QuickSort(a,q+1,r); 12 } 13 }
上述代码中的6-8行是一个随机选取哨兵的过程,因为如果我们的一个序列是逆序,我们每次将第一个元素作为哨兵,则每次排序将序列分出一单元素的序列,需要进行n次排序,这样的时间复杂度为O(n^2),要降低时间复杂度就得保证每次选取的哨兵是一个中间数,使用随机数效果可能会好一点,但并不能保证选取就是中间数,为进一步改善结果,我们可以使用三数取中法,即挑出序列的三个数,我们将其排序,选取中间的那个数作为哨兵。将上面的6-8行代码改为:
1 int mid = p + (r - p) / 2; 2 if (a[p] > a[mid]) 3 Swap(a[p], a[mid]); 4 if (a[mid] > a[r]) 5 Swap(a[mid], a[r]); 6 if (a[p] > a[mid]) 7 Swap(a[p], a[mid]); 8 Swap(a[p], a[mid]);
1-7行经过3次比较交换后,a[mid]成为中间数,然后将其与第一个数交换(第8行),此时的哨兵便成了3个数的中间数。此时快速排序的时间复杂度为O(nlogn),它的空间复杂度为O(logn),同时它是一个不稳定的排序。
6. 计数排序
计数排序的基本思想:如果我们要对一个长为n的序列A排序,使用一个辅助数组C[n]来记录A中每个元素出现的次数,进一步计算出记录A中小于元素n的个数,利用数组B来输出排序结果,具体代码如下:
1 void CountSort(vector<int> A, vector<int>& B) 2 { 3 int n = A.size(); 4 int max = 0; 5 for (int i = 0; i < n; i++) 6 { 7 if (max < A[i]) 8 max = A[i]; 9 } 10 int len = max + 1; 11 vector<int> C(len, 0); 12 for (int j = 0; j<n; j++) 13 C[A[j]]=C[A[j]]+1; 14 for (int m = 1; m<len; m++) 15 C[m]=C[m]+C[m-1]; 16 for (int i = n - 1; i >= 0; i--) 17 { 18 B[C[A[i]]-1]=A[i]; 19 C[A[i]]=C[A[i]]-1; 20 } 21 }
这里我们要求A中的元素大小为0到某个正数,C的大小为A中的最大数加1,这样C中的坐标索引就对应了A中的每一个元素,代码12,13行实现了用容器C来存储A中每个数出现的次数,14,15行则记录了小于数m的个数,假设为n,而m对应A中的一个数,这个数排在第n位。16到20行实现元素的排序,之所以从后向前排,是为了保证稳定性。我们假设输入序列A为 1,4,3,4,3,A的大小为5,则B的大小也应该为5,A的最大值为4,C的大小为4+1=5,C[0]记录A中0的个数,也为0,C[1]记录A中1的个数,等于1,同理C[2]=0,C[3]=2,C[4]=2.
进一步计算C[1]=C[0]+C[1]=1,表示小于等于1的个数,C[2]=C[2]+C[1]=1,表示小于等于2的个数,C[3]=3,C[4]=5.计算完毕之后开始排序,我们从A中的最后一个元素开始,即A[4]=3,因为C[3]=3,即A中小于等于A[4]的数有3个,则应将A[4]排在B中的第三位,即第18行代码,排好后A中小于等于3的数就少了一个,将其中C中的记录数减一,即第19行代码,这样能够保证前后相等的数不会发生交换,实现了排序的稳定性。通过循环对A的其他数进行排序,得到最终结果。
该算法的时间复杂度为O(n),但如果A中的数很大时,明显要花费很大的空间,那么如何处理大范围的数?
我们可以使用计数排序的方法从低位到高位来进行排序,这种方法又叫基数排序,我们以三位数为例,进行排序:
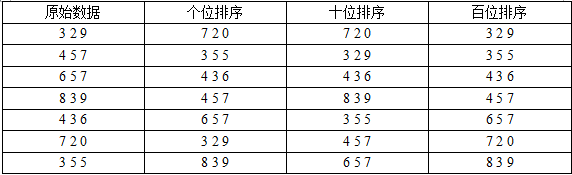
如上图所示,我们可以从最低位开始排序,然后依次将高位排序,最后得到一个有序的序列,如果数比较大,位数多,我们可以考虑将连续的n位作为一个整体进行计数排序。总之要同时兼顾时间复杂度与空间复杂度。
7. 总结
各种算法的时间复杂度、空间复杂度与稳定性如下表所示:
