一:贝塞尔曲线是什么
利用三点控制,生成一条平滑的曲线,具体解析看这个贝塞尔曲线扫盲
二:使用canvas绘制小球沿贝塞尔曲线运动
贝塞尔曲线由三个点确定,起始点P0,中间点(控制点)P1,和终点P2。确定三个点之后,用canvas所有的quadraticCurveTo方法绘制二阶贝塞尔曲线,小球的运动路径就出现了。但是小球需要沿着曲线运动,小球的运动是一帧一帧的,每一帧处于不同的点位置,所以需要计算出一定间隔的点坐标集合,然后根据集合,改变小球的位置坐标,从而达到小球沿曲线运动的效果。
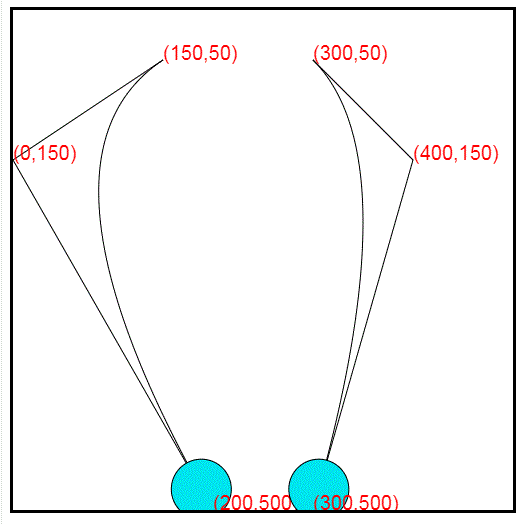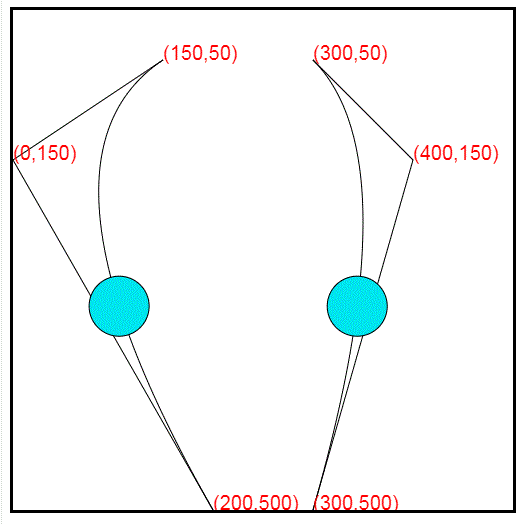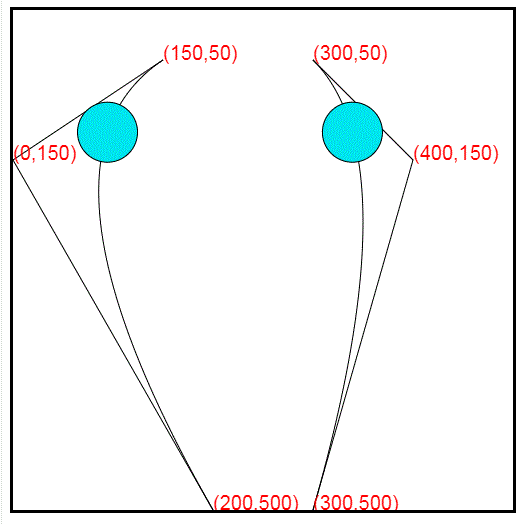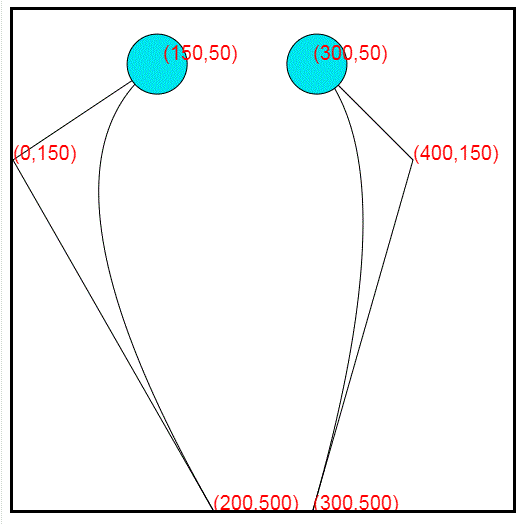
1.canvas 绘制贝塞尔二阶曲线
quadraticCurveTo方法是canvas自带的绘制贝塞尔二阶曲线公式,传入控制点和终点,画出曲线
function draw_curve(obj) {
//绘制2次贝塞尔曲线
context.beginPath();
context.moveTo(obj.p0_x,obj.p0_y);/*开始点*/
context.quadraticCurveTo(obj.p1_x,obj.p1_y,obj.p2_x,obj.p2_y);/*前两个是控制点坐标xy,后两个是结束点坐标xy*/
context.strokeStyle = "#000";
context.stroke();
context.closePath();
}2.利用贝塞尔二阶曲线公式计算出曲线某点坐标
我们知道了三点,起始点P0,中间点(控制点)P1,和终点P2。
二阶曲线公式为B(t) = (1-t)^2 P0 + 2(1-t)tP1+ t^2P2;
这里的t是从0到0.99的数,可以取间隔0.01递增
当t为0.05时候,曲线上面某点的坐标O(Ox,Oy)的计算为
Ox = (1-t)^2 P0x + 2(1-t)tP1x+ t^2P2x;
Oy = (1-t)^2 P0y + 2(1-t)tP1y+ t^2P2y;
//利用贝塞尔曲线公式计算出曲线上某点坐标
function get_bezier_dot(t,obj){
var x = (1-t)*(1-t)*obj.p0_x + 2*t*(1-t)*obj.p1_x + t*t*obj.p2_x;
var y = (1-t)*(1-t)*obj.p0_y + 2*t*(1-t)*obj.p1_y + t*t*obj.p2_y;
return {x:x,y:y}
}3.画圆方法,传入位置坐标
function draw_ball(x,y) {
context.beginPath();
context.fillStyle = '#00E5EE';
context.arc(x, y,30, 0, Math.PI * 2);
context.fill();
context.stroke();
context.closePath();
}4.每一帧动画动画执行流程draw_frame()
(1)传入t,计算出这个曲线t时刻的点坐标,利用贝塞尔二阶公式get_bezier_dot()
(2)绘制贝塞尔曲线用quadraticCurveTo()
(3)根据(1)得到的坐标点用context.arc()画出此时的圆在canvas上面
(4)可以再画出坐标文字在图上context.fillText(text, x, y);
5.整体运动轨迹流程:
(1)每隔一定时间间隔画一帧的内容setInterval()
(2)清空画布,清空上一帧的画布clearRect()
(3)传入t,计算出坐标O',根据O'的坐标位置画此帧的内容,即上面每帧的动画流程draw_frame()
(4)此时t增加0.01,当t>0.99的时候clearInterval()
(5)运动完成