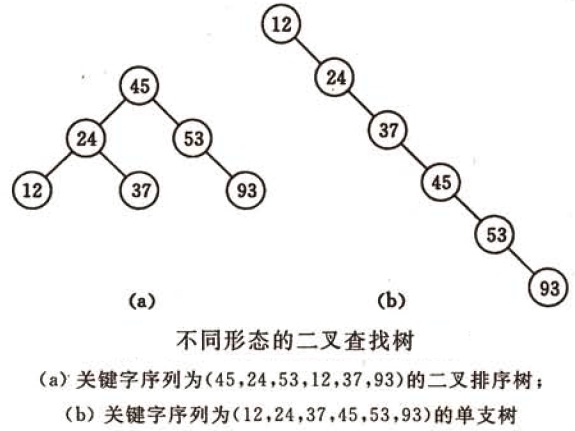
1、二叉树
二叉树(Binary Tree)的特点是每个结点至多具有两棵子树(即在二叉树中不存在度大于2的结点),并且子树之间有左右之分。
二叉树的性质:
(1)、在二叉树的第i层上至多有2i-1个结点(i≥1)。
(2)、深度为k的二叉树至多有2k-1个结点(k≥1)。
(3)、对任何一棵二叉树,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
一棵深度为k且有2k-1个结点的二叉树称为满二叉树。
可以对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右,则由此可引出完全二叉树的定义。深度为k且有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时,称之为完全二叉树。
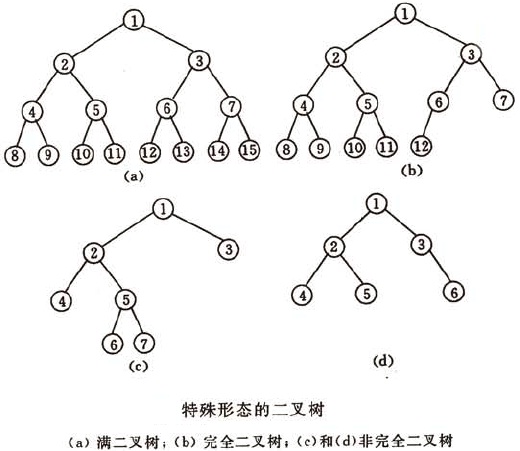
(4)、具有n个结点的完全二叉树的深度为不大于log2n的最大整数加1。
(5)、如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到最后一层,每层从左到右),则对任一结点i(1≤i≤n),有
a、如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点x(其中x是不大于i/2的最大整数)。
b、如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
c、如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
二叉树的链式存储:
链式二叉树中的每个结点至少需要包含三个域,数据域和左、右指针域。

二叉树的遍历:
假如以L、D、R分别表示遍历左子树、访问根结点和遍历右子树,则可有DLR、DRL、LRD、LDR、RLD、RDL这六种遍历二叉树的方案。若限定先左后右,则只有三种方案,分别称之为先(根)序遍历、中(根)序遍历和后(根)序遍历,它们以访问根结点的次序来区分。
2、二叉查找树
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
- 中序遍历二叉查找树可得到一个关键字的有序序列。
- 删除
删除某个结点后依然要保持二叉查找树的特性。例子中的删除过程如下:
a、若删除点是叶子结点,则设置其双亲结点的指针为空。
b、若删除点只有左子树,或只有右子树,则设置其双亲结点的指针指向左子树或右子树。
c、若删除点的左右子树均不为空,则:
1)、查询删除点的右子树的左子树是否为空,若为空,则把删除点的左子树设为删除点的右子树的左子树。
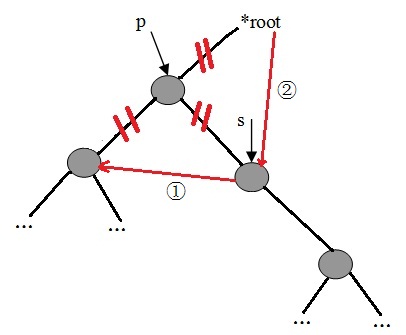
2)、若不为空,则继续查询左子树,直到找到最底层的左子树为止。
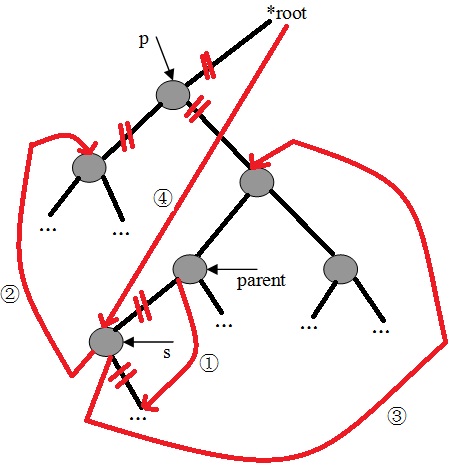
- 二叉查找树的查找分析
同样的关键字,以不同的插入顺序,会产生不同形态的二叉查找树。
运行两次,以不同的顺序输入相同的六个关键字:
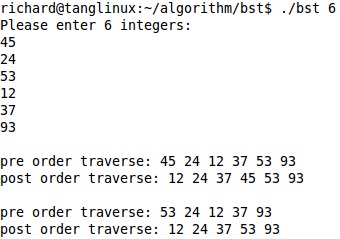

根据前序遍历的结果可得到两次运行所产生的二叉查找树的形态并不相同,如下图: