题目:树网的核
网址:https://www.luogu.com.cn/problem/P1099
题目描述
设(T=(V,E,W))是一个无圈且连通的无向图(也称为无根树),每条边到有正整数的权,我们称(T)为树网(treenetwork),其中(V,E)分别表示结点与边的集合,(W)表示各边长度的集合,并设(T)有(n)个结点。
路径:树网中任何两结点(a,b)都存在唯一的一条简单路径,用(d(a,b))表示以(a,b)为端点的路径的长度,它是该路径上各边长度之和。我们称(d(a,b))为(a,b)两结点间的距离。
(D(v,P)=min{d(v,u)}),(u)为路径(P)上的结点。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网(T),直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心举(mathrm{ECC}):树网(T)中距路径(F)最远的结点到路径(F)的距离,即
(mathrm{ECC}(F)=max{d(v, F),v in V})
任务:对于给定的树网(T=(V, E, W))和非负整数(s),求一个路径(F),他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过(s)(可以等于(s)),使偏心距(ECC(F))最小。我们称这个路径为树网(T=(V, E, W))的核(Core)。必要时,(F)可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
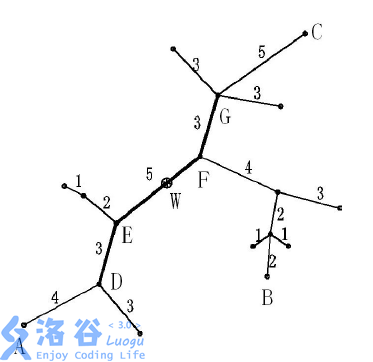
下面的图给出了树网的一个实例。图中,(A-B)与(A-C)是两条直径,长度均为(20)。点(W)是树网的中心,(EF)边的长度为(5)。如果指定(s=11),则树网的核为路径(DEFG)(也可以取为路径(DEF)),偏心距为(8)。如果指定(s=0)(或(s=1)、(s=2)),则树网的核为结点(F),偏心距为(12)。
输入格式
共(n)行。
第(1)行,两个正整数(n)和(s),中间用一个空格隔开。其中(n)为树网结点的个数,(s)为树网的核的长度的上界。设结点编号以此为(1,2dots,n)。
从第(2)行到第(n)行,每行给出(3)个用空格隔开的正整数(u,v,w),依次表示每一条边的两个端点编号和长度。
输出格式
一个非负整数,为指定意义下的最小偏心距。
输入输出样例
输入 #1
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出 #1
5
输入 #2
8 6
1 3 2
2 3 2
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3
输出 #2
5
说明/提示
- 对于(40\%)的数据,保证(n le 15)。
- 对于(70\%)的数据,保证(n le 80)。
- 对于(100\%)的数据,保证(n le 300),(0le sle10^3),(1 leq u, v leq n),(1 leq w leq 10^3)。
关于树的直径有几条推论:
- 一棵树的直径大于等于一条(显然);
- 树的所有直径必定交于树的中心(结论1);
- 树的直径上最小偏心距相等(结论2);
我们给出证明:
我只需证明两条直径即可。
设直径长为(d),两条直径(d_1)、(d_2)。
结论1的证明
先证明所有直径必然相交:
若不相交,由于一棵树,两条直径必然在同一联通块内。故(d_1)上必然存在一点(s),(d_2)上必然存在一点(t),(s),(t)连通;
我们考虑(s)将(d_1)分成的两部分(p_1,p_2),(t)将(d_2)分成两部分(p_3,p_4),则(max(p_1,p_2)+max(p_3,p_4)>=d),而(s)和(t)距离大于等于(1),则说明存在一条经过(s)和(t)比直径还长的路,矛盾!
再证明交点必然有树的中心:
树的直径具有最长性,也就是说任意一条直径外的点到直径上的任意一个点都不会超过直径两端点到一个点的距离。如果(d_1)交(d_2)于非中心结点,那么从直径两端点出发到另外的两端点距离一定比树的直径大。所以交点必然在树的中心处。
证毕。
结论2的证明
若两条直径交于一点,则最小偏心距一定是直径的两端点上取得;
若重叠一条链,重叠的那部分对于任意一颗直径平权。
下证,直径分叉(实在不会说了)部分不会影响结论正确。
由于直径的性质,分叉总长度一定小于(d)(可以等于只不过是三条了),而直径外的结点到分叉的距离一定小于“分叉”长,故答案一定通过树的直径一个端点取到。
为了便于理解,我们考虑下面:

(1)号结点一定对答案产生了影响,而分叉不会对答案产生影响(可以画图看看)。
证毕。
于是,我们有以下做法:
算法1(朴素 + 贪心)
找一条直径,在上面枚举子区间。
贪心可知:区间长度越长越好。
C ++ AC代码
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
const int SIZE = 500000 + 10;
vector <int> G[SIZE], W[SIZE];
vector <int> path;
queue <int> Q;
bool vis[SIZE];
int n, s, ver1 = -1, ver2 = -1, ans = 1 << 30, dp[SIZE], dis[SIZE], prev[SIZE], q[SIZE];
void bfs()
{
while(!Q.empty()) Q.pop();
memset(dis, -1, sizeof(dis));
Q.push(1);
dis[1] = 0;
int val = -1;
while(Q.size())
{
int u = Q.front();
Q.pop();
for(int i = 0; i < G[u].size(); ++ i)
{
int v = G[u][i], w = W[u][i];
if(dis[v] == -1)
{
dis[v] = dis[u] + w;
if(dis[v] > val)
{
val = dis[v];
ver1 = v;
}
Q.push(v);
}
}
}
val = -1;
memset(dis, -1, sizeof(dis));
Q.push(ver1);
dis[ver1] = 0;
while(Q.size())
{
int u = Q.front();
Q.pop();
for(int i = 0; i < G[u].size(); ++ i)
{
int v = G[u][i], w = W[u][i];
if(dis[v] == -1)
{
dis[v] = dis[u] + w;
prev[v] = u;
if(dis[v] > val)
{
val = dis[v];
ver2 = v;
}
Q.push(v);
}
}
}
int u = ver2;
path.clear();
path.push_back(ver2);
while(u != ver1)
{
u = prev[u];
path.push_back(u);
}
reverse(path.begin(), path.end());
return;
}
int est(int u)
{
memset(dp, -1, sizeof(dp));
Q.push(u);
dp[u] = 0;
int now, num = -1;
while(Q.size())
{
now = Q.front();
Q.pop();
for(int i = 0; i < G[now].size(); ++ i)
{
int v = G[now][i], w = W[now][i];
if(vis[v] || dp[v] != -1) continue;
dp[v] = dp[now] + w;
if(dp[v] > num) num = dp[v];
Q.push(v);
}
}
return num;
}
void work()
{
int head = 0, tail = 0, u;
for(int i = 0; i < path.size(); ++ i)
{
u = path[i];
while(head < tail && dis[u] - dis[q[head]] > s)
{
vis[q[head]] = false;
++ head;
}
q[tail ++] = u;
vis[u] = true;
int tmp = 0;
for(int j = head; j < tail; ++ j)
{
tmp = max(tmp, est(q[j]));
}
ans = min(ans, tmp);
}
return;
}
int main()
{
scanf("%d %d", &n, &s);
for(int i = 1; i <= n; ++ i)
{
G[i].clear();
W[i].clear();
}
for(int i = 1; i < n; ++ i)
{
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
G[u].push_back(v), G[v].push_back(u);
W[u].push_back(w), W[v].push_back(w);
}
bfs();
work();
printf("%d
", ans);
return 0;
}
算法2(直接扫描)
偏心距可以有区间上每个点到最远的非直径上的点距离和直径端点距离进行更新即可。
C ++ AC代码
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
const int SIZE = 500000 + 10;
vector <int> G[SIZE], W[SIZE];
vector <int> path;
queue <int> Q;
bool vis[SIZE];
int n, s, ver1 = -1, ver2 = -1, ans = 1 << 30, d[SIZE], dp[SIZE], dis[SIZE], prev[SIZE], q[SIZE];
void bfs()
{
while(!Q.empty()) Q.pop();
memset(dis, -1, sizeof(dis));
Q.push(1);
dis[1] = 0;
int val = -1;
while(Q.size())
{
int u = Q.front();
Q.pop();
for(int i = 0; i < G[u].size(); ++ i)
{
int v = G[u][i], w = W[u][i];
if(dis[v] == -1)
{
dis[v] = dis[u] + w;
if(dis[v] > val)
{
val = dis[v];
ver1 = v;
}
Q.push(v);
}
}
}
val = -1;
memset(dis, -1, sizeof(dis));
Q.push(ver1);
dis[ver1] = 0;
while(Q.size())
{
int u = Q.front();
Q.pop();
for(int i = 0; i < G[u].size(); ++ i)
{
int v = G[u][i], w = W[u][i];
if(dis[v] == -1)
{
dis[v] = dis[u] + w;
prev[v] = u;
if(dis[v] > val)
{
val = dis[v];
ver2 = v;
}
Q.push(v);
}
}
}
int u = ver2;
path.clear();
path.push_back(ver2);
while(u != ver1)
{
u = prev[u];
path.push_back(u);
}
reverse(path.begin(), path.end());
return;
}
int calc(int u)
{
int val = -1, now, v;
memset(dp, -1, sizeof(dp));
dp[u] = 0;
Q.push(u);
while(Q.size())
{
now = Q.front();
Q.pop();
for(int i = 0; i < G[now].size(); ++ i)
{
int v = G[now][i], w = W[now][i];
if(dp[v] == -1)
{
dp[v] = dp[u] + w;
if(!vis[v] && dp[v] > val) val = dp[v];
Q.push(v);
}
}
}
return val;
}
void work()
{
for(int i = 0; i < path.size(); ++ i) vis[path[i]] = true;
int num = -1;
for(int i = 0; i < path.size(); ++ i) num = max(num, calc(path[i]));
int head = 0, tail = 0, u, tmp;
for(int i = 0; i < path.size(); ++ i)
{
u = path[i];
while(head < tail && dis[u] - dis[q[head]] > s) ++ head;
q[tail ++] = u;
tmp = max(num, max(dis[q[head]] - dis[ver1], dis[ver2] - dis[u]));
ans = min(ans, tmp);
}
return;
}
int main()
{
scanf("%d %d", &n, &s);
for(int i = 1; i <= n; ++ i)
{
G[i].clear();
W[i].clear();
}
for(int i = 1; i < n; ++ i)
{
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
G[u].push_back(v), G[v].push_back(u);
W[u].push_back(w), W[v].push_back(w);
}
bfs();
work();
printf("%d
", ans);
return 0;
}
总结回顾
这道题费了我很大劲,但是最终我明白了直径性质,并给出适当的证明。