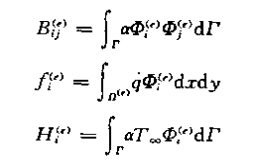我们知道,有限元求解是有流程套路的
1. 伽辽金求解+Green-Guass公式。纽曼边界条件会自然满足,不需要后续边界条件修正
2. 对于三角形单元,我们一般采用面积坐标进行映射求解。对于二维矩形单元则采用与矩形中心点坐标有关的映射,映射结果为一个积分区间为【-1,1】,【-1,1】的边长为2的正方形。

3.选择插值函数:一阶插值的公式为

4.将插值函数代入计算即可。
5.对于矩形单元的二阶插值函数计算公式为

6.这里补充一下边界条件的修正,纽曼边界条件自然满足,第一类边界条件需要将边界点编号所在的刚度矩阵中的行和列变为0,对角线设为1,同时对载荷矩阵进行相应修改。这两个是比较简单的边界条件。对于第三类边界条件,其施加方法为:
如下为计算最后的积分方程,其中Bij和Hi为需要计算的边界上的积分函数。我们知道,即使在边界,也是靠一个个的小单元的边界围起来的。所以第三类边界条件不是像第一类边界条件那样对单个节点的值进行操作,而是以边为单位,一次计算由连续两个节点组成的一个单元的某条边的积分。并且计算时也采用线坐标进行映射,这样计算比较方便。需要注意的是,边界在单元中的位置不同,结果也不同,如在每个单元内,节点的单元编号分1,2,3,如果边界边为单元的节点12边,计算结果与节点23边,13边是不同的。对于边12,phi1=1-epsilon;phi2=epsilon;phi3=0。看下面的图可以进一步理解。