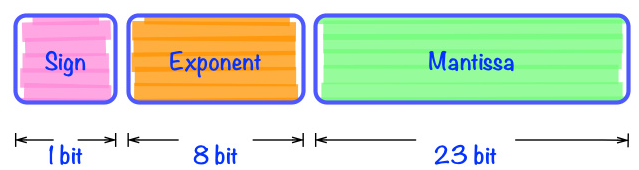
0.28+0.34=?
我相信这个简单的加法,谁都会,肯定等于0.62嘛。
这是两个特别简单的加法,那如果我在其整数位置上加上其他的数字,或者多加几个和项,你是否还能快速算过来?
我想这时候,我们又得借助计算器了!而这,有时可能就是电脑!尤其是如果咱们借助简单程序语言来算的时候,嘿嘿,可能就不是那么回事了~
不信你看,用javascript算的结果:
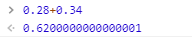
用python算的结果:
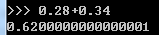
当然了,我尝试着用其他语言来试一下,结果好像并不都是这样。
其中,java只会在类型转换的时候出现奇怪的值:(当然这在我们写代码时往往很容易这么干)

好了,前言就到此为止!咱们是要来看一下,为什么 1+1不等于2 ?
其实这是由浮点数在计算机中的存储方式决定的,因为计算机只认识0101,所以小数点的保存就需要使用另外的算法来转换了,大概如下:(以下内容参考网络知识库)
计算机中是用有限的连续字节保存浮点数的。 保存这些浮点数当然必须有特定的格式, C/C++中的浮点数类型 float 和 double 采纳了 IEEE 754 标准中所定义的单精度 32 位浮点数和双精度 64 位浮点数的格式。 在 IEEE 标准中,浮点数是将特定长度的连续字节的所有二进制位分割为特定宽度的符号域,指数域和尾数域三个域, 其中保存的值分别用于表示给定二进制浮点数中的符号,指数和尾数。 这样,通过尾数和可以调节的指数(所以称为"浮点")就可以表达给定的数值了。
32位浮点数存储结构如下:
三个主要成分是:
- Sign(1bit):表示浮点数是正数还是负数。0表示正数,1表示负数
- Exponent(8bits):指数部分。类似于科学技术法中的M*10^N中的N,只不过这里是以2为底数而不是10。需要注意的是,这部分中是以2^7-1即127,也即01111111代表2^0,转换时需要根据127作偏移调整。
- Mantissa(23bits):基数部分。浮点数具体数值的实际表示。
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
V = (-1)^s×M×2^E
(1)(-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
(2)M表示有效数字,大于等于1,小于2,但整数部分的1可以省略。
(3)2^E表示指数位。比如:
对于十进制的5.25对应的二进制为:101.01,相当于:1.0101*2^2。所以,S为0,M为1.0101,E为2。
而-5.25=-101.01=-1.0101*2^2.。所以S为1,M为1.0101,E为2。
浮点数是如何存储的,来看另一篇文章的简单解说(https://www.cnblogs.com/yiyide266/p/7987037.html):
Step 1 改写整数部分
以数值5.2为例。先不考虑指数部分,我们先单纯的将十进制数改写成二进制。
整数部分很简单,5.即101.。Step 2 改写小数部分
小数部分我们相当于拆成是2^-1一直到2^-N的和。例如:
0.2 = 0.125+0.0625+0.007825+0.00390625即2^-3+2^-4+2^-7+2^-8….,也即.00110011001100110011。或者换个更傻瓜的方式去解读十进制对二进制小数的改写转换,通常十进制的0.5也(也就是分数1/2),相当于二进制的0.1(同等于分数1/2),
我们可以把十进制的小数部分乘以2,取整数部分作为二进制的一位,剩余小数继续乘以2,直至不存在剩余小数为止。
例如0.2可以转换为:
0.2 x 2 = 0.4 0
0.4 x 2 = 0.8 0
0.8 x 2 = 1.6 1
0.6 x 2 = 1.2 1
0.2 x 2 = 0.4 0
0.4 x 2 = 0.8 0
0.8 x 2 = 1.6 1
.......
即:.0011001.......(它是一个4862的无限循环的二进制数,明白为什么十进制小数转换成二进制小数的时候为什么会出现精度损失的情况了吗)
Step 3 规格化
现在我们已经有了这么一串二进制101.00110011001100110011。然后我们要将它规格化,也叫Normalize。其实原理很简单就是保证小数点前只有一个bit。于是我们就得到了以下表示:1.0100110011001100110011 * 2^2。到此为止我们已经把改写工作完成,接下来就是要把bit填充到三个组成部分中去了。Step 4 填充
指数部分(Exponent):之前说过需要以127作为偏移量调整。因此2的2次方,指数部分偏移成2+127即129,表示成10000001填入。
整数部分(Mantissa):除了简单的填入外,需要特别解释的地方是1.010011中的整数部分1在填充时被舍去了。因为规格化后的数值整部部分总是为1。那大家可能有疑问了,省略整数部分后岂不是1.010011和0.010011就混淆了么?其实并不会,如果你仔细看下后者:会发现他并不是一个规格化的二进制,可以改写成1.0011 * 2^-2。所以省略小数点前的一个bit不会造成任何两个浮点数的混淆。
好了,看完上面的浮点数的存储原理后,是时候来解答,为什么计算机会算错的问题了!
1. 遇到小数点后数字转换为实际存储结构时,有的转换是一个死循环,即不可能得到一个精确的值,而这个不精确的值再与其他数据做运算时,得到的结果自然也就可能存在差距了。至于有时候能得到准确的数值,有时候却得不到准备的值,则是和逆转换相关了(即内存结构转换为可视的十进制数据)!
2. 另一个存在误差的原因,则是因为在计算过程中进行了数据类型的转换,因为原数据本来就不是精确的值,所以在进行类型转换后,就不会得到和原始值直接转化的值的相同结果了。
所以,咱们在做需要高精度的计算场合时,使用计算机语言自带的存储结构可能会不满足咱们的需求,当然这也很容易办到,一般也会有第三方的解决方案,即换一种存储结构就可能能解决这种问题了。
如 java 中,使用 BigDecimal 来解决需要高精度运算的场景。(BigDecimal的解决方案就是,不使用二进制,而是使用十进制(BigInteger)+小数点位置(scale)来表示小数);BigDecimal应使用string构造更为准确,否则会在第一步转换时出现精度丢失!
最后,附几个加法结果以供参观:
>> 57168.619999999995-11087.28 46081.34 >> 2412.02+11087.64+8338.28+5580.0 27417.940000000002 >> 0.28+0.34 0.6200000000000001 >> 2.28+2.34 4.619999999999999 >> 33.28+3.34 36.620000000000005 >> 3.28+3.34 6.619999999999999 >> 4.28+4.34 8.620000000000001 >> 5.28+5.34 10.620000000000001 >> 8.28+8.34 16.619999999999997 >> 33.28+9.34 42.620000000000005