Description
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 $n$个结点和 $n-1$条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从$1$到$n$的连续正整数。
现在有$m$个玩家,第$i$个玩家的起点为 $S_i$,终点为 $T_i$ 。每天打卡任务开始时,所有玩家在第$0$秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点$j$的观察员会选择在第$W_j$秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第$W_j$秒也理到达了结点 $j$ 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点$j$作为终点的玩家: 若他在第$W_j$秒前到达终点,则在结点$j$的观察员不能观察到该玩家;若他正好在第$W_j$秒到达终点,则在结点$j$的观察员可以观察到这个玩家。
Input
第一行有两个整数$n$和$m$ 。其中$n$代表树的结点数量, 同时也是观察员的数量, $m$代表玩家的数量。
接下来 $n- 1$行每行两个整数$u$和 $v$,表示结点 $u$到结点 $v$有一条边。
接下来一行 $n$个整数,其中第$j$个整数为$W_j$ , 表示结点$j$出现观察员的时间。
接下来 $m$行,每行两个整数$S_i$,和$T_i$,表示一个玩家的起点和终点。
对于所有的数据,保证$1leq S_i,T_ileq n, 0leq W_jleq n$ 。
Output
输出1行 $n$个整数,第$j$个整数表示结点$j$的观察员可以观察到多少人。
Sample Input
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
Sample Output
2 0 0 1 1 1
Hint
Solution
我们一档一档部分分来看。
因为下面要跟随测试点贴代码,这里先把main函数和预处理部分贴出
#include<vector>
#include<cstdio>
#include<algorithm>
#define rg register
#define ci const int
#define cl const long long int
typedef long long int ll;
namespace IO {
char buf[90];
}
template<typename T>
inline void qr(T &x) {
char ch=getchar(),lst=' ';
while(ch>'9'||ch<'0') lst=ch,ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
if(lst=='-') x=-x;
}
template<typename T>
inline void write(T x,const char aft,const bool pt) {
if(x<0) x=-x,putchar('-');
int top=0;
do {
IO::buf[++top]=x%10+'0';
x/=10;
} while(x);
while(top) putchar(IO::buf[top--]);
if(pt) putchar(aft);
}
template<typename T>
inline T mmax(const T a,const T b) {if(a>b) return a;return b;}
template<typename T>
inline T mmin(const T a,const T b) {if(a<b) return a;return b;}
template<typename T>
inline T mabs(const T a) {if(a<0) return -a;return a;}
template<typename T>
inline void mswap(T &a,T &b) {
T temp=a;a=b;b=temp;
}
const int maxn = 1000010;
const int maxm = 1000010;
const int ZAY = 300004;
struct Edge {
int to,nxt;
};
Edge edge[maxm];int hd[maxn],ecnt;
inline void cont(ci from,ci to) {
Edge &e=edge[++ecnt];
e.to=to;e.nxt=hd[from];hd[from]=ecnt;
}
struct M {
int s,t,an,sum,tk;
inline bool operator<(const M &_others) const {
return this->sum < _others.sum;
}
};
M MU[maxn];
struct W {
int v,num,ans;
inline bool operator<(const W &_others) const {
return this->v < _others.v;
}
};
W w[maxn];
struct C {
int ud,v,tp;
C (int _ud=0,int _v=0,int _tp=0) {ud=_ud,v=_v,tp=_tp;}
};
std::vector<C>cg[maxn];
int n,m;
int deepth[maxn],fa[maxn],LCA[30][maxn],pos[maxn],lft[maxn],rt[maxn];
void t1();
void s1();
void lian();
void baoli();
void zhengjie();
void dfs(ci,ci);
int ask(int,int);
int dfsearch(ci,ci);
void deepfs(ci,ci);
void dfirsts(ci,ci);
inline bool cmp(const W &_a,const W & _b) {
return _a.num < _b.num;
}
int main() {
qr(n);qr(m);
rg int a,b;
for(rg int i=1;i<n;++i) {
a=b=0;qr(a);qr(b);
cont(a,b);cont(b,a);
}
for(rg int i=1;i<=n;++i) {
qr(w[i].v);w[i].num=i;
}
for(rg int i=1;i<=m;++i) {
qr(MU[i].s);qr(MU[i].t);
}
int _num=n%10;
if(_num < 4) baoli();
else if(_num == 4) lian();
else if(_num == 5) s1();
else if(_num == 6) t1();
else zhengjie();
return 0;
}
void dfs(ci u,ci fat) {
deepth[u]=deepth[fa[u]=fat]+1;
LCA[0][u]=fat;
for(rg int i=0;LCA[i][u];++i) {
LCA[i+1][u]=LCA[i][LCA[i][u]];
}
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
dfs(edge[i].to,u);
}
int ask(int x,int y) {
if(deepth[x] < deepth[y]) mswap(x,y);
rg int delta=deepth[x]-deepth[y];
for(rg int i=25;delta;--i) if(delta & (1<<i)) {
x=LCA[i][x],delta^=(1<<i);
}
if(x == y) return x;
for(rg int i=25;i != -1;--i) if(LCA[i][x] != LCA[i][y]) {
x=LCA[i][x],y=LCA[i][y];
}
return LCA[0][x];
}
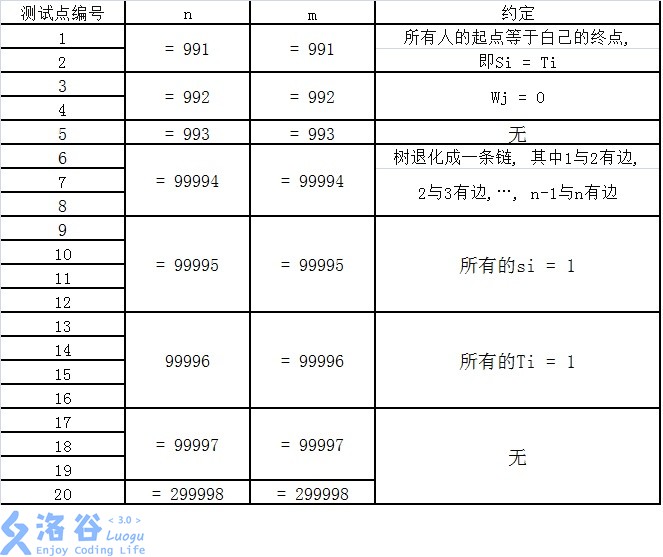
测试点$1、2$
起点和终点相同,那么只会在第零秒被观测到。那么对于所有$W_j=0$的点统计有多少条路径为这个点即可。期望得分$10$分
测试点$3、4$
每个观察员都是0,所以直接对每条路径起点的计数器++即可。期望得分$20$分
测试点$5$
发现秒数不超过1000,可以暴力枚举每一秒,在每一秒暴力枚举每个玩家在什么位置。具体的,对每条路径求LCA。对于每个玩家,如果当前时间比起点到LCA的距离小,那么点$u$的位置变成$father[u]$。否则若当前是第$k$秒,则他的位置是终点$t$向上$l-k-1$个深度。其中$l$是路径长度。期望得分$25$分
测试点$6、7、8$
当树是一条链的时候,发现从$s$出发只有向左和向右两种可能。具体的,$s~leq~t$则向右,否则向左。考虑对于在点$j$的观察员,不妨设被他观察的玩家向右行走(向左同理),则有 (s+w_j=j) 移项可得 (s=j-W_j) 类似的对向左行走的满足 (s=j+W_j) 这样的计数问题显然是需要桶的。有两种方法通过这几个测试点。
1 排序
将每个点按照观察员出现的时间排序,把所有$s$压入桶中,将每条路径按照长度排序。枚举每个观察员出现的时间,对于第$j$个观察员,它的答案即为$lft[j+w_j]+rt[j-w_j]$,每过一个时刻删除桶中已经到终点的路径。由于一共有$n$个观察员,每条路径被枚举$1$次,共$n$次。加上排序,时间复杂度为$O(nlogn)$。
void lian() {
for(rg int i=1;i<=m;++i) {
if(MU[i].t >= MU[i].s) ++rt[MU[i].s],MU[i].sum=MU[i].t-MU[i].s;
else ++lft[MU[i].s],MU[i].sum=MU[i].s-MU[i].t;
}
std::sort(MU+1,MU+1+m);
std::sort(w+1,w+1+n);
rg int j=0;
for(rg int i=1;i<=n;++i) {
while(j <= m) {
if(MU[j].sum >= w[i].v) break;
if(MU[j].s <= MU[j].t) --rt[MU[j].s];
else --lft[MU[j].s];
++j;
}
int _d=w[i].num-w[i].v;
if(_d > 0) w[i].ans+=rt[_d];
_d=w[i].num+w[i].v;
if(_d <= n) w[i].ans+=lft[_d];
}
std::sort(w+1,w+1+n,cmp);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
2 差分
直接扫描整条链。先从左向右扫描。对于一个点$i$,向桶中加入会从该点出发的向右的路径条数。对于每个终点,把所有终点为它的向右的路径的起点位置的桶$--$。这样对于每个点统计答案时统计的就是当前合法(没有结束)的节点$s$的个数。然后从右向左扫描,方法同理。扫描结束后可以得到答案。 复杂度$O(n)$。
期望得分40分。
测试点$9$~$12$
这4个测试点起点都是1。我们不妨钦定这棵树1是根 对于每个点$j$的观察员,能观察到点显然当且仅当$w_j==deepth_j$。那么他能观察到的点的个数显然是它子树中的终点个数。直接dfs统计即可。
void s1() {
deepth[0]=-1;
dfs(1,0);
for(rg int i=1;i<=m;++i) {
++lft[MU[i].t];
}
int _cnt=dfsearch(1,0);
if(!w[1].v) w[1].ans=_cnt;
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
int dfsearch(ci u,ci fat) {
rg int _cnt=lft[u];
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
_cnt+=dfsearch(edge[i].to,u);
if(w[u].v == deepth[u]) w[u].ans=_cnt;
return _cnt;
}
测试点$13$~$16$
这些测试点的终点是1。依然不妨钦定1为根。 考虑一个点$j$能看到一条路径$i$显然该路径的起点是$j$的子树并且$w_j+deepth_j=l$,其中$l$为链长。这样依然可以dfs统计$j$的子树的信息。这里有一个小技巧:对于一个全局的桶,如果想使用它记录一次dfs对答案的贡献,则在进入dfs时记录初始量,dfs结束时求最终量,中间的增量即为这次dfs对答案的贡献。在这里增量就是$j$的子树中满足上式的链的条数。
void deepfs(ci u,ci fat) {
rg int _c=lft[w[u].v+deepth[u]+ZAY];
lft[deepth[u]+ZAY]+=rt[u];
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
deepfs(edge[i].to,u);
w[u].ans=lft[w[u].v+deepth[u]+ZAY]-_c;
}
void t1() {
deepth[0]=-1;
for(rg int i=1;i<=m;++i) ++rt[MU[i].s];
dfs(1,0);
deepfs(1,0);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
测试点$17$~$20$
把上面的思路整理一下。刚才的起点和终点分别为根已经提示我们将路径分为向上走的和向下走的两种。对于向上走的,一个玩家能被点$j$看见的必要条件是$deepth_j+w_j=deepth_s$,其中s是起点 对于向下走的玩家,能被$j$的必要条件是$deepth_j+w_j=deepth_t-l+1$,其中$l$为链长t是终点。注意到上面的条件都是必要条件,一个玩家被保证能看见需要保证该路径经过该点。这样我们可以dfs对于每个点统计经过他的路径中的答案。如果快速的对不合法的路径进行删除呢?考虑是链的部分带给我们的思路,对于一条路径,我们将其分为向上的为$s$到$LCA的儿子$,向下的为$LCA$到$t$。这样对于向上的在$s$处对桶中的答案$(,在LCA处(LCA的儿子的父亲)对答案)--$。向下的路径在$t$处对桶中的答案$$,在$LCA$的父亲处$--$。即可通过本题
void zhengjie() {
dfs(1,0);
for(rg int i=1;i<=n;++i) {
MU[i].an=ask(MU[i].s,MU[i].t);
MU[i].sum=deepth[MU[i].s]-2*deepth[MU[i].an]+deepth[MU[i].t]+1;
cg[MU[i].s].push_back(C(1,deepth[MU[i].s],1));
cg[MU[i].t].push_back(C(2,deepth[MU[i].t]-MU[i].sum+1+ZAY,1));
cg[MU[i].an].push_back(C(1,deepth[MU[i].s],-1));
cg[fa[MU[i].an]].push_back(C(2,deepth[MU[i].t]-MU[i].sum+1+ZAY,-1));
}
dfirsts(1,0);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
void dfirsts(ci u,ci fat) {
int _temp=lft[deepth[u]+w[u].v]+rt[deepth[u]-w[u].v+ZAY];
rg unsigned int _s=cg[u].size();
for(rg unsigned i=0;i<_s;++i) {
int _ud=cg[u][i].ud;
if(_ud == 1) {
lft[cg[u][i].v]+=cg[u][i].tp;
}
else rt[cg[u][i].v]+=cg[u][i].tp;
}
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
dfirsts(edge[i].to,u);
w[u].ans=lft[deepth[u]+w[u].v]+rt[deepth[u]-w[u].v+ZAY]-_temp;
}
Code
这其中包含所有的部分分。事实上直接跑正解即可
#include<vector>
#include<cstdio>
#include<algorithm>
#define rg register
#define ci const int
#define cl const long long int
typedef long long int ll;
namespace IO {
char buf[90];
}
template<typename T>
inline void qr(T &x) {
char ch=getchar(),lst=' ';
while(ch>'9'||ch<'0') lst=ch,ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
if(lst=='-') x=-x;
}
template<typename T>
inline void write(T x,const char aft,const bool pt) {
if(x<0) x=-x,putchar('-');
int top=0;
do {
IO::buf[++top]=x%10+'0';
x/=10;
} while(x);
while(top) putchar(IO::buf[top--]);
if(pt) putchar(aft);
}
template<typename T>
inline T mmax(const T a,const T b) {if(a>b) return a;return b;}
template<typename T>
inline T mmin(const T a,const T b) {if(a<b) return a;return b;}
template<typename T>
inline T mabs(const T a) {if(a<0) return -a;return a;}
template<typename T>
inline void mswap(T &a,T &b) {
T temp=a;a=b;b=temp;
}
const int maxn = 1000010;
const int maxm = 1000010;
const int ZAY = 300004;
struct Edge {
int to,nxt;
};
Edge edge[maxm];int hd[maxn],ecnt;
inline void cont(ci from,ci to) {
Edge &e=edge[++ecnt];
e.to=to;e.nxt=hd[from];hd[from]=ecnt;
}
struct M {
int s,t,an,sum,tk;
inline bool operator<(const M &_others) const {
return this->sum < _others.sum;
}
};
M MU[maxn];
struct W {
int v,num,ans;
inline bool operator<(const W &_others) const {
return this->v < _others.v;
}
};
W w[maxn];
struct C {
int ud,v,tp;
C (int _ud=0,int _v=0,int _tp=0) {ud=_ud,v=_v,tp=_tp;}
};
std::vector<C>cg[maxn];
int n,m;
int deepth[maxn],fa[maxn],LCA[30][maxn],pos[maxn],lft[maxn],rt[maxn];
void t1();
void s1();
void lian();
void baoli();
void zhengjie();
void dfs(ci,ci);
int ask(int,int);
int dfsearch(ci,ci);
void deepfs(ci,ci);
void dfirsts(ci,ci);
inline bool cmp(const W &_a,const W & _b) {
return _a.num < _b.num;
}
int main() {
qr(n);qr(m);
rg int a,b;
for(rg int i=1;i<n;++i) {
a=b=0;qr(a);qr(b);
cont(a,b);cont(b,a);
}
for(rg int i=1;i<=n;++i) {
qr(w[i].v);w[i].num=i;
}
for(rg int i=1;i<=m;++i) {
qr(MU[i].s);qr(MU[i].t);
}
/* int _num=n%10;
if(_num < 4) baoli();
else if(_num == 4) lian();
else if(_num == 5) s1();
else if(_num == 6) t1();
else */zhengjie();
return 0;
}
void dfs(ci u,ci fat) {
deepth[u]=deepth[fa[u]=fat]+1;
LCA[0][u]=fat;
for(rg int i=0;LCA[i][u];++i) {
LCA[i+1][u]=LCA[i][LCA[i][u]];
}
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
dfs(edge[i].to,u);
}
int ask(int x,int y) {
if(deepth[x] < deepth[y]) mswap(x,y);
rg int delta=deepth[x]-deepth[y];
for(rg int i=25;delta;--i) if(delta & (1<<i)) {
x=LCA[i][x],delta^=(1<<i);
}
if(x == y) return x;
for(rg int i=25;i != -1;--i) if(LCA[i][x] != LCA[i][y]) {
x=LCA[i][x],y=LCA[i][y];
}
return LCA[0][x];
}
void baoli() {
dfs(1,0);
for(rg int i=1;i<=m;++i) {
MU[i].an=ask(MU[i].s,MU[i].t);
pos[i]=MU[i].s;
}
std::sort(w+1,w+1+n);
rg int j=1;
for(rg int i=0;i<n;++i) {
while(j <= n) {
if(w[j].v != i) break;
for(rg int k=1;k<=m;++k) if(pos[k] == w[j].num) ++w[j].ans;
++j;
}
for(rg int k=1;k<=m;++k) if(deepth[MU[k].s]+deepth[MU[k].t]-2*deepth[MU[k].an] > i) {
int _d=deepth[MU[k].s]-deepth[MU[k].an];
if(_d > i) {
pos[k]=fa[pos[k]];
}
else {
_d=deepth[MU[k].s]-deepth[MU[k].an]+deepth[MU[k].t]-deepth[MU[k].an]-i-1;
int _t=MU[k].t;
for(rg int h=25;_d;--h) if(_d & (1<<h)) {
_t=LCA[h][_t],_d^=(1<<h);
}
pos[k]=_t;
}
}
else pos[k]=0;
}
while(j <= n) {
for(rg int k=1;k<=m;++k) if(pos[k] == w[j].num) ++w[j].ans;
++j;
}
std::sort(w+1,w+1+n,cmp);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
void lian() {
for(rg int i=1;i<=m;++i) {
if(MU[i].t >= MU[i].s) ++rt[MU[i].s],MU[i].sum=MU[i].t-MU[i].s;
else ++lft[MU[i].s],MU[i].sum=MU[i].s-MU[i].t;
}
std::sort(MU+1,MU+1+m);
std::sort(w+1,w+1+n);
rg int j=0;
for(rg int i=1;i<=n;++i) {
while(j <= m) {
if(MU[j].sum >= w[i].v) break;
if(MU[j].s <= MU[j].t) --rt[MU[j].s];
else --lft[MU[j].s];
++j;
}
int _d=w[i].num-w[i].v;
if(_d > 0) w[i].ans+=rt[_d];
_d=w[i].num+w[i].v;
if(_d <= n) w[i].ans+=lft[_d];
}
std::sort(w+1,w+1+n,cmp);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
void s1() {
deepth[0]=-1;
dfs(1,0);
for(rg int i=1;i<=m;++i) {
++lft[MU[i].t];
}
int _cnt=dfsearch(1,0);
if(!w[1].v) w[1].ans=_cnt;
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
int dfsearch(ci u,ci fat) {
rg int _cnt=lft[u];
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
_cnt+=dfsearch(edge[i].to,u);
if(w[u].v == deepth[u]) w[u].ans=_cnt;
return _cnt;
}
void deepfs(ci u,ci fat) {
rg int _c=lft[w[u].v+deepth[u]+ZAY];
lft[deepth[u]+ZAY]+=rt[u];
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
deepfs(edge[i].to,u);
w[u].ans=lft[w[u].v+deepth[u]+ZAY]-_c;
}
void t1() {
deepth[0]=-1;
for(rg int i=1;i<=m;++i) ++rt[MU[i].s];
dfs(1,0);
deepfs(1,0);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
void zhengjie() {
dfs(1,0);
for(rg int i=1;i<=n;++i) {
MU[i].an=ask(MU[i].s,MU[i].t);
MU[i].sum=deepth[MU[i].s]-2*deepth[MU[i].an]+deepth[MU[i].t]+1;
cg[MU[i].s].push_back(C(1,deepth[MU[i].s],1));
cg[MU[i].t].push_back(C(2,deepth[MU[i].t]-MU[i].sum+1+ZAY,1));
cg[MU[i].an].push_back(C(1,deepth[MU[i].s],-1));
cg[fa[MU[i].an]].push_back(C(2,deepth[MU[i].t]-MU[i].sum+1+ZAY,-1));
}
dfirsts(1,0);
for(rg int i=1;i<n;++i) write(w[i].ans,' ',true);
write(w[n].ans,'
',true);
}
void dfirsts(ci u,ci fat) {
int _temp=lft[deepth[u]+w[u].v]+rt[deepth[u]-w[u].v+ZAY];
rg unsigned int _s=cg[u].size();
for(rg unsigned i=0;i<_s;++i) {
int _ud=cg[u][i].ud;
if(_ud == 1) {
lft[cg[u][i].v]+=cg[u][i].tp;
}
else rt[cg[u][i].v]+=cg[u][i].tp;
}
for(rg int i=hd[u];i;i=edge[i].nxt) if(edge[i].to != fat)
dfirsts(edge[i].to,u);
w[u].ans=lft[deepth[u]+w[u].v]+rt[deepth[u]-w[u].v+ZAY]-_temp;
}
Summary
1、树上操作问题在单点进行加减操作时常考虑使用差分进行完成 2、根据部分分推到正解是一种非常不错的姿势 3、对于全局桶的应用:记录它对某次计算的贡献可以统计他的增量。