容斥原理:在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。------百度百科
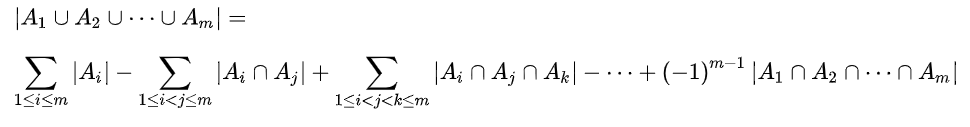
从中可以得出一个简单的规律:“奇加偶减”,即加上所有奇数个集合的交集;减去所有偶数个集合的交集,所得结果为A1到Am的并集。
根据这个规律,利用二进制表示集合的选择,编程即可。

解题思路:枚举每个k,可以知道小于n的k次幂的个数为 n^(1/k);又知道: (a^b)^c = a^(b*c),因为合数可以分解为多个质数的乘积,所以仅枚举质数即可。
但是一个数既可以是a次幂的表示,也可以是b次幂的表示,所以统计会有重复,利用容斥,“奇加偶减”。
10^18<2^60,所以枚举60以内的质数即可。
源码:
#include<iostream> #include<cstring> #include<cmath> using namespace std; typedef long long ll; const int maxn=60; const double eps=1e-8; int prime[maxn+1]; void getPrime() //计算出60以内的质数 { memset(prime,0,sizeof(prime)); for(int i=2;i<=maxn;i++){ if(!prime[i])prime[++prime[0]]=i; for(int j=1;j<=prime[0]&&prime[j]*i<=maxn;j++){ prime[prime[j]*i]=1; if(i%prime[j]==0)break; } } } int main() { getPrime(); ll n; while(cin>>n){ ll ans=0; for(unsigned i=1;i<(1LL<<prime[0]);i++){ //二进制产生集合的选择 ll num=0,mul=1; for(int j=0;j<prime[0];j++){ if((i>>j)&1)mul*=prime[j+1],num++; } ll tmp=(ll)(pow((double)n,1.0/mul)+eps)-1; //计算当k=mul时小于n的个数 if(num&1)ans+=tmp; else ans-=tmp; } cout<<ans+1<<endl; } return 0; }