中缀表达式转后缀表达式

1.中缀表达式

　　当我们编写诸如 A * B 之类的算术表达式时，表达式的形式提供了我们该如何解释表达式的信息。在这种情况下，我们知道变量 B 乘以变量 C ，

因为乘法运算符 * 出现在表达式中它们之间。这种表示法称为中缀表达式，因为运算符位于它正在处理的两个操作数之间。

　　考虑另一个中缀示例，A + B * C。运算符 + 和 * 仍然出现在操作数之间，但是问题却出现了。他们在哪些操作数上工作？+ 是在 A 和 B 上工作，

还是 * 在 B 和 C 上？表达似乎含糊不清。

　　事实上，因为我们一直在和中缀表达式打交道，所以这不会给我们带来任何问题。我们知道，每个运算符都有一个优先级。优先级较高的运算符在

优先级较低的运算符之前计算。唯一可以改变运算顺序的是就是括号。乘法和除法的运算优先级要要高于加法和减法。如果出现两个具有相同优先级的

运算符，则从左到右依次运算。

　　让我们使用运算符优先级来计算“麻烦”的表达式 A + B * C。首先将 B 和 C 相乘，然后 A 再和它们的乘积相加。( A + B ) * C 将计算乘法之前，

强制先计算 A + B 。在表达式 A + B + C中，通过依次计算，最左边的 + 将首先完成。

2.完全括号表达式

　　虽然这一切对我们来说显而易见，但请记住，计算机需要确切知道要执行的操作符以及执行的顺序。编写表达式以保证操作顺序不会混淆的一种方法

是创建所谓的完全括号表达式。这种类型的表达式为每个运算符使用一对括号。括号决定了操作的顺序，没有歧义，也没有必要记住任何优先规则。

　　表达式 A + B * C + D 可以重写为（（A +（B * C））+ D）以表示首先发生乘法，然后是最左边的加法。A + B + C + D可写为 (((A + B) + C) + D) ，

因为加法操作从左到右依次计算的。

3.前缀和后缀表达式

　　还有另外两种非常重要的表达格式，一开始可能看起来不太明显。考虑中缀表达式 A + B 。如果我们把运算符移动到操作数之前？结果表达式将是

+ A B。同样，我们可以将运算符移动到最后，我们会得到 A B +，这看起来有点奇怪。

　　这些对操作符相对于操作数的位置的更改创建了两种新的表达格式，前缀和后缀。前缀表达式表示法要求所有运算符都在它们处理的两个操作数之前。

另一方面，后缀表达式要求其运算符位于相应的操作数之后。还有一些例子应该有助于使这一点更清晰（见表1）。

A + B * C 在前缀中写为 + A * B C。乘法运算符紧接在操作数 B 和 C 之前，表示 * 优先于 +。然后，加法运算符出现在 A 和乘法结果之前。

在后缀中，表达式为ABC * +。同样，操作的顺序被保留，因为 * 紧跟在 B 和 C 之后出现，表示 * 具有优先权，其后为 + 。尽管运算符移动并且现在出现在

它们各自操作数之前或之后，但操作数的顺序相对于彼此保持完全相同。

　　现在考虑中缀表达式（A + B）* C。回想一下，在这种情况下，中缀要求括号在乘法之前强制执行加法。但是，当 A + B 用前缀写入时，加法运算符只是

移动到了操作数之前，+ A B，此操作的结果成为乘法的第一个操作数。乘法运算符移动到了整个表达式前面，得到* + A B C。同样，在后缀 A B + 中强制先执行加法。

然后对结果和剩余的操作数C进行乘法，最后，得到的后缀表达式是 A B + C *。

　　再次考虑这三个表达式（见表2）。发生了一些非常重要的事情。括号去哪儿了？为什么我们不需要在前缀和后缀中使用它们？答案是，运算符对于它们所处理的操作数

不再模棱两可。只有中缀表示法需要附加符号。前缀和后缀表达式中的操作顺序完全取决于运算符的位置，而不是其他任何内容。在许多方面，这使得中缀成为使用中最不理想的符号。

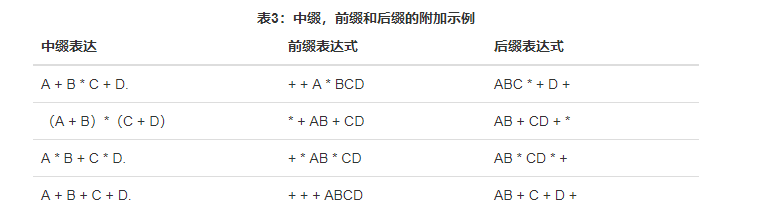
　　表3显示了中缀表达式以及等效前缀和后缀表达式的一些其他示例。请确保您了解它们在执行操作的顺序方面是如何等效的

4.将中缀表达式转换为前缀和后缀

　　到目前为止，我们已使用手动方法在中缀表达式和等效前缀和后缀表达式表示法之间进行转换。正如您所料，有一些算法可以执行转换，允许任何复杂的表达式被正确转换。

我们将考虑的第一种技术使用前面讨论过的完全括号表达式的概念。回想一下，A + B * C 可写为A +（B * C）），以明确显示乘法优先于加法。然而，仔细观察，您可以看

到每个括号对也表示操作数对的开头和结尾，中间有相应的运算符。

　　查看上面子表达式（B * C）中的右括号。如果我们将乘法符号移动到该位置并删除匹配的左括号，给我们BC * ，我们实际上已经将子表达式转换为后缀表示法。如果加法

运算符也被移动到其对应的右括号位置并且删除了匹配的左括号，则将产生完整的后缀表达式（参见图1）。

　　　　　　　　　　　　　　　　　　　　　　　　　　图1：向右移动运算符以生成后缀表示法

　　如果我们做同样的事情，但不是将符号移动到右括号的位置，我们将它移到左边，我们得到前缀表示法（见图2）。括号对的位置实际上是封闭运算符最终位置的线索。

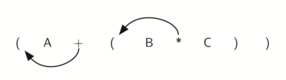
图2：将复杂表达式转换为前缀和后缀表示法

5.中缀到后缀转换算法

　　我们需要开发一种算法，将任何中缀表达式转换为后缀表达式。为此，我们将仔细研究转换过程。

　　再次考虑表达式A + B * C 。如上所示，ABC * + 是后缀等价物。我们已经注意到操作数 A ， B 和 C 保持在它们的相对位置。改变位置的只是运算符。让我们再看一下中缀表达式中的运算符。

从左到右显示的第一个运算符是 + 。但是，在后缀表达式中， + 是最后的，因为下一个运算符 * 优先于加法。原始表达式中的运算符的顺序在生成的后缀表达式中相反。

　　当我们处理表达式时，操作符必须保存在某处，因为它们还没有看到相应的右操作数。此外，由于它们的优先级，这些保存的运算符的顺序可能需要反转。这个例子中的加法和乘法就是

这种情况。由于加法运算符位于乘法运算符之前且优先级较低，因此需要在使用乘法运算符之后出现。由于这种顺序的逆转，考虑使用堆栈来保持运算符直到需要它们是有意义的。

　　A + B）* C 怎么样？回想一下，AB + C * 是后缀等价物。再次，从左到右处理这个中缀表达式，我们首先看到 + 。在这种情况下，当我们看到 * 时， + 已经被放置在结果表达式中，因为它

凭借括号优先于 * 。

　　我们现在可以开始了解转换算法的工作原理。当我们看到左括号时，我们将保存它以表示另一个具有高优先级的运算符将会到来。该运算符需要等到对应的右括号出现，当右括号确实出现时，

可以从堆栈中弹出操作符。当我们从左到右扫描中缀表达式时，我们将使用堆栈来保留运算符。这将提供我们在第一个例子中提到的逆转。堆栈顶部始终是最近保存的运算符。每当我们读取一个

新的运算符时，我们都需要考虑该运算符如何优先于堆栈上的运算符（如果有的话）进行比较。

以下步骤将中缀表达式转换成后缀表达式。

创建一个空栈opstack，用于保持运算符。为输出创建一个空字符串。
从左到右扫描字符串。
- 如果字符是操作数，则将其附加到输出列表的末尾。
- 如果字符是左括号，请将其压栈入opstack。
- 如果字符是右括号，则弹出opstack直到遇到相应的左括号。并将每个弹出的运算符附加到输出字符串的末尾。
- 如果字符是操作符， * ， / ， + 或 - ，请将其入栈到 opstack。但是，首先弹出opstack上具有更高或相同优先级的任何运算符，并将这些运算符加到输出字符串。
扫描字符串完字符串后，检查 opstack。任何仍在堆栈上的运算符都可以删除并附加到输出字符串的末尾。

下图显示了对表达式A * B + C * D 进行处理的转换算法。请注意，第一个 * 运算符在看到 + 运算符时被删除。此外，当第二个 * 出现时， + 停留在堆栈上，因为乘法优先于加法。在中缀表达式的末尾，

堆栈弹出两次，删除两个运算符并将 + 作为后缀表达式中的最后一个运算符。

#include<bits/stdc++.h> 
using namespace std; 
  
// 返回操作符的优先级 
int prec(char c) { 
    if(c == '^') 
    return 3; 
    else if(c == '*' || c == '/') 
    return 2; 
    else if(c == '+' || c == '-') 
    return 1; 
    else
    return -1; 
} 
  
// 将中缀表达式转换为后缀表达式主程序 
void infixToPostfix(string s) { 
    stack<char> st; 
    int l = s.length(); 
    string ns; 
    for(int i = 0; i < l; i++) { 
        // 如果扫描到的字符是操作数，直接加到输出字符串中
        if((s[i] >= 'a' && s[i] <= 'z')||(s[i] >= 'A' && s[i] <= 'Z'))  ns+=s[i]; 
        //  如果扫描到的字符是 ‘( ’, 则 ‘( ’入栈 
        else if(s[i] == '(')  st.push('('); 
        // 如果扫描到的字符是 ‘ )’, 则一直出栈，并加到输出字符串中
        // 直到遇到 ‘ (’ 
        else if(s[i] == ')') { 
            while(!st.empty() && st.top() != '(') { 
                char c = st.top(); 
                st.pop(); 
                ns += c; 
            } 
            if(st.top() == '(') { 
                char c = st.top(); 
                st.pop(); 
            } 
        } 
          
        // 如果扫描到的字符是运算符 
        else{ 
            while(!st.empty() && prec(s[i]) <= prec(st.top())) { 
                char c = st.top(); 
                st.pop(); 
                ns += c; 
            } 
            st.push(s[i]); 
        } 
  
    } 
    
    // 出栈剩下的运算符, 并加入到输出字符串中 
    while(!st.empty()) { 
        char c = st.top(); 
        st.pop(); 
        ns += c; 
    } 
      
    cout << ns << endl; 
} 
  
int main() { 
    string exp = "a+b*(c^d-e)^(f+g*h)-i"; 
    infixToPostfix(exp); 
    return 0; 
}