有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
多重背包问题只是相当于将完全背包问题中的物品可用次数由无限变为了有限。
1、最简单算法:
1 include<iostream> 2 #include<algorithm> 3 using namespace std; 4 const int array_size = 101; 5 int f[array_size], N, V, v, w, s; 6 struct Goods { 7 int v, w; 8 }; 9 int main() { 10 cin >> N >> V; 11 for (int i = 0; i < N; ++i) { 12 cin >> v >> w >> s; 13 for(int j=V;j>=0;--j) 14 for(int k=1;k<=s&&k*v<=j;++k) 15 f[j] = max(f[j], f[j - k * v] + k * w); //逐个比较选用0-s个物品 16 } 17 cout << f[V]; 18 }
2、二进制优化方法,时间复杂度:o(N*logS*V)
1 #include<iostream> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 struct Good { 6 int vi, wi; 7 }; 8 const int array_size = 2001; 9 int f[array_size], N, V, v, w, s; 10 vector<Good> vessel; 11 /* 12 二进制优化方法 13 v,w,s 14 每个物品拆成s份,最多需要log(s)个数来表示 15 例:某物品共7个,可由1,2,4(pow(2,k))组合 16 分别把1个物品,2个物品,4个物品当作1组, 17 即将7个物品分为3个物品,其体积与价值分别为: 18 v,w;2*v,2*w;4*v,4*w。转化为01背包问题。 19 */ 20 int main() { 21 cin >> N >> V; 22 for (int i = 0; i < N; ++i) { 23 cin >> v >> w >> s; 24 for (int k = 1; k <= s; k *= 2) { 25 s -= k; 26 vessel.push_back({ k * v,k * w }); 27 } 28 if (s > 0) 29 vessel.push_back({ s * v,s * w }); 30 } 31 //01背包问题算法 32 for (Good good : vessel) 33 for (int j = V; j >= good.vi; --j) 34 f[j] = max(f[j], f[j - good.vi] + good.wi); 35 cout << f[V]; 36 }
3、单调队列优化方法
单调队列:单调队列维护的是下标。作用是得到当前序列长度为"m"的子序列中的最小值或最大值的下标。单调队列只有递增和递减两种队列。
一定要记住,单调队列push进去的是原序列的下标而非值。当push一个下标"i"时: (1)当deque.front()<=i-m时,pop之; (2)当f[deque.back()]>f[i]时,pop之,再大再pop之,不大为止; (3)push下标"i"。 最后deque.front()就是当前序列长度为"m"的子序列中的最小值。
对于本题来说,用到的是单调递减队列:
在一个物品加入的过程中,f[j]只可能被f[j−v],f[j−2∗v]…f[j−s∗v]更新掉。
所以我们可以余数相同的j分开处理。
发现对于一个f[j],能更新它的值是这样的:
f[j]=max(f[j−v]+v,f[j−2∗v]+2∗w,f[j−3∗v]+3∗w…)
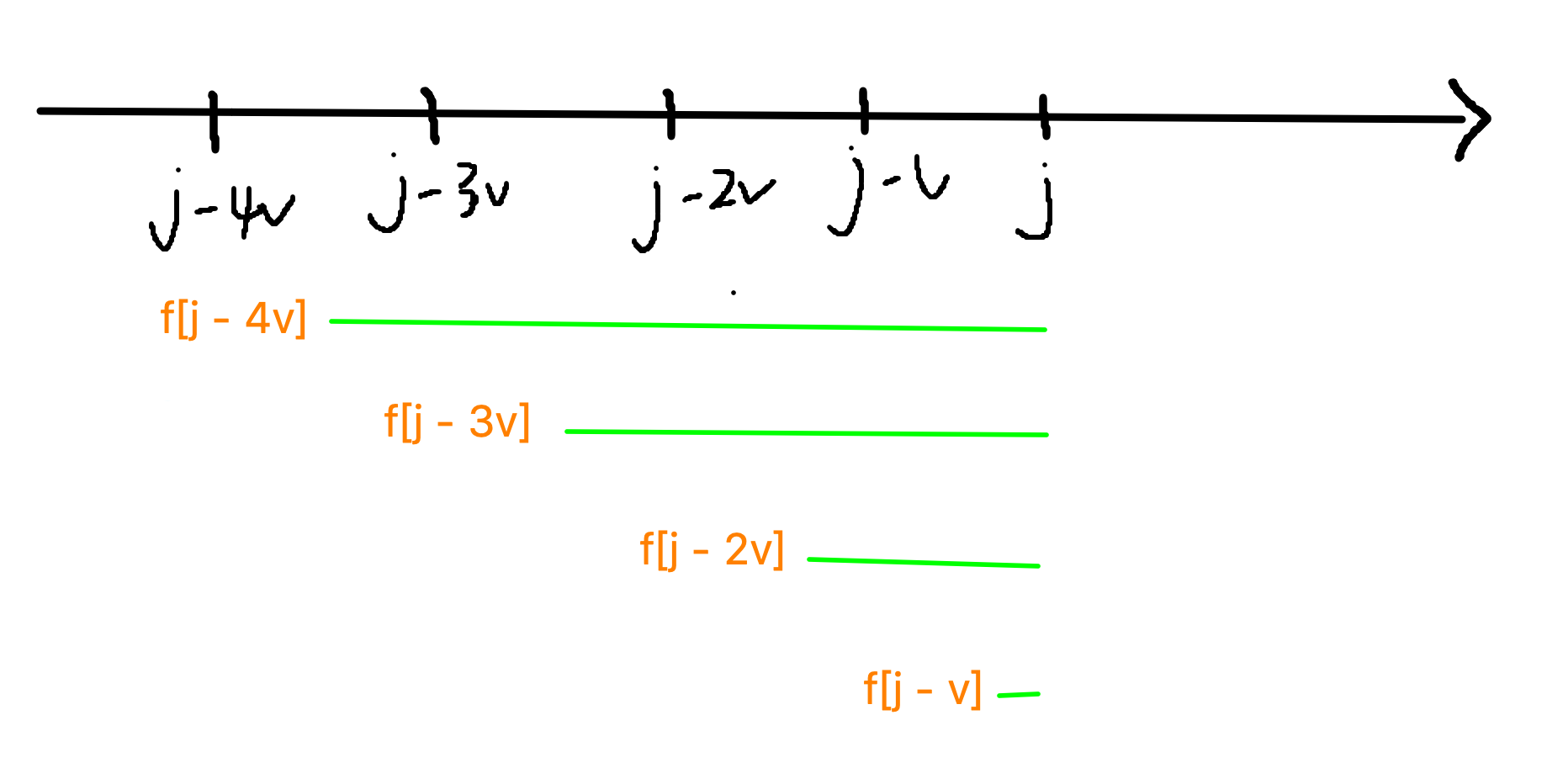
感性理解一下,橙色部分 + 绿色部分。
我们发现,在j转变成j+v后,绿色部分伸长的距离是等长的。
所以,我们比较它们的时候可以减掉一个对应部分,让他们在同一个起跑线上
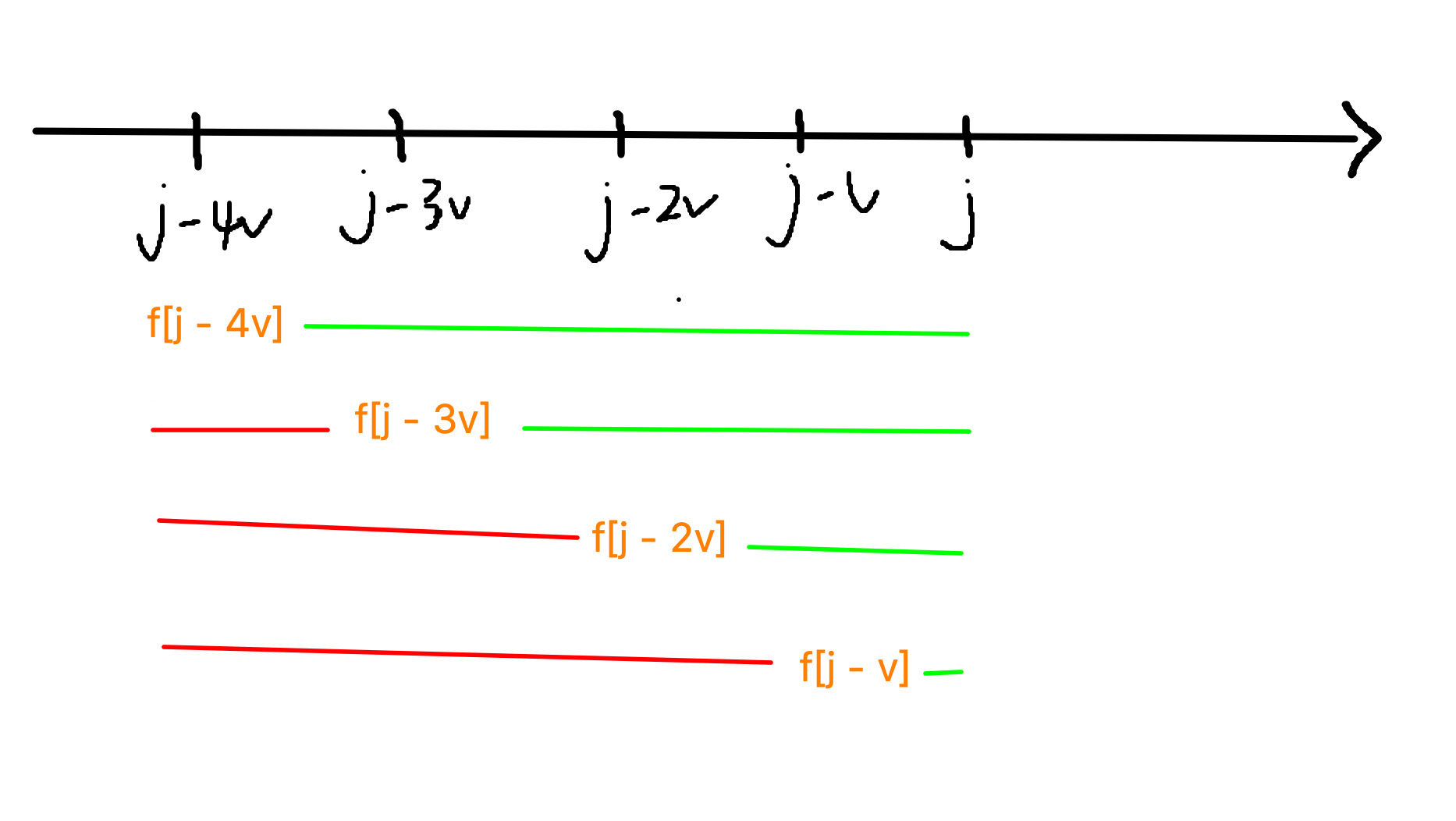
y总的代码即减掉了红色部分。
这样在j增长的过程中,队列中元素的相对大小不会变,即队头元素更新肯定是最优的。
#include<iostream> #include<algorithm> using namespace std; /* f:前i个物品,背包容积0-V,对应的最大价值 g:前i-1个物品,背包容积0-V,对应的最大价值 q:单调递减队列 */ const int array_size = 20001; int f[array_size], g[array_size], q[array_size], N, V, v, w, s; int main() { cin >> N >> V; for (int i = 0; i < N; ++i) { cin >> v >> w >> s; copy(f, f + array_size, g); for (int j = 0; j < v; ++j) { int hh = 0, tt = -1;//分别表示队首、队尾 for (int k = j; k <= V; k += v) { if (hh <= tt && q[hh] + s * v < k) ++hh; //取出队首元素,队列首部当前子序列范围内一定是最大值的下标 //队列不为空且队尾元素对应的值<=新插入元素对应的值 while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) --tt; //剔除队列中一定不会用到的元素 q[++tt] = k; //push新值的下标 if (hh <= tt) //队列不为空 f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w); //用最大值更新一下f[k] } } } cout << f[V]; }