题面
https://www.luogu.com.cn/problem/P4720
题解
Lucas算法,能够在p为质数的情况下快速计算出组合数%p的值。
相关链接: https://blog.csdn.net/raalghul/article/details/51752369
扩展Lucas算法(exLucas)则不要求p为质数,但是此种情况下p不能很大,大致在1e6左右。
利用算术基本定理,设(p=prod_{i=1}^{k}{p_i^{alpha_i}}),其中(p_1<p_2<…<p_k)为素数,(alpha_iin Z^*(1<=i<=k))。
容易想到对每一个(i {in} [1,k]),求出 ({R_i}={ binom{n}{m}} mod {p_i}^{alpha_i})再用中国剩余定理合并。
先将组合数拆分成三个阶乘。
此时无法使用逆元求解,因为这三个阶乘都有可能与(p_i)不互质,从而不存在逆元。
考虑分离阶乘中的(p_i)。
只需知道(v_{p_i}(n!),v_{p_i}(m!),v_{p_i}((n-m)!))(其中({v_{p_i}}(n))表示n的素因数分解式中(p_i)的幂次)
以及({frac{n!}{p_i^{v_{p_i}(n!)}}},{frac{m!}{p_i^{v_{p_i}(m!)}}},{frac{(n-m)!}{p_i^{v_{p_i}((n-m)!)}}})共6项,就可以前后3项分别合并,然后得出(R_i)了。
结论:(v_{p_i}(n!) = {sum_{j=1}^{+infty}}{lfloor}{frac{n}{{p_i}^j}}{ floor})
很好理解,右边表示的是([1,n])间(p_i,p_i^2,…)的倍数数量之和。一个([1,n])间、恰被(p_i^t)整除的数对左边的贡献是t,在右边也正好被计入了t次
那么前三项易求。后三项表示的含义是n!、m!、(n-m)!中不断除去(p_i),直到不整除为止,最后剩下的部分。设(g(n))表示({frac{n!}{p^{v_{p_i}(n!)}}}{mod{p_i^{alpha_i}}}),我们想要求(g(n),g(m))和(g(n-m))。
为此,我们可以先预处理出(f(1))~(f(p_i^{alpha_i})),其中(f(x))表示([1,x])中所有与(p_i)互质的数的乘积对(p_i^{alpha_i})取模的结果。下以求g(n)为例,我们可以将1到n每(p_i)个数一行,列在一个表格中:
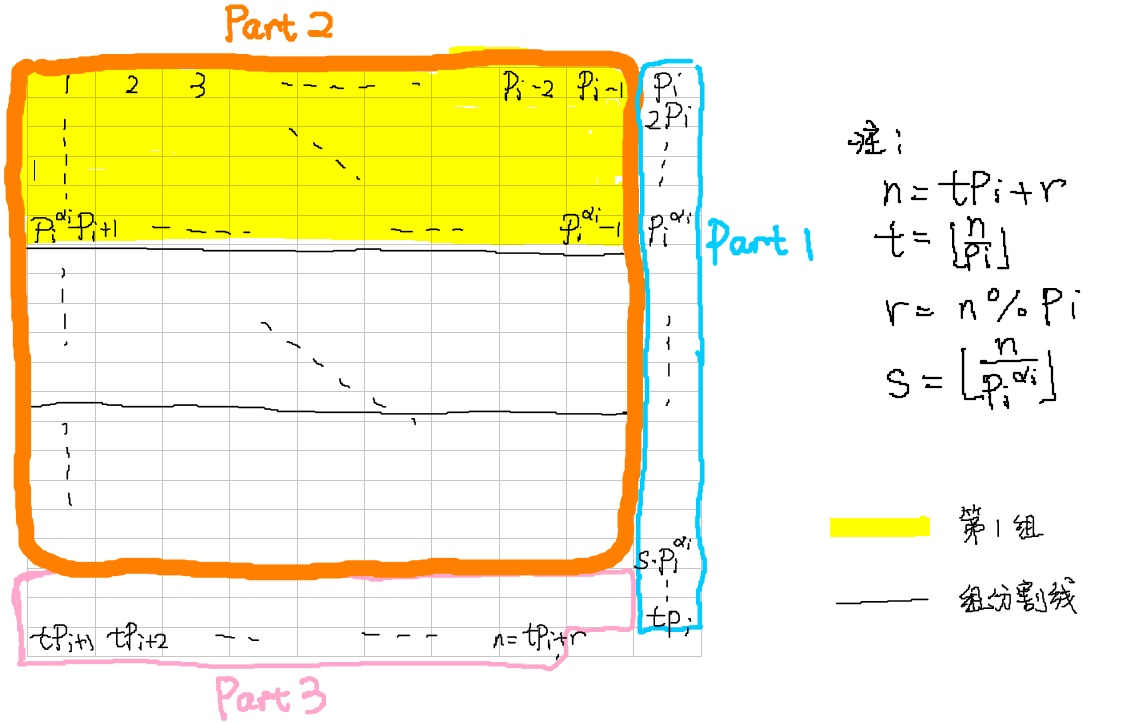
- t,r,s的意义已经标注在表格右边。
那么这个表格可以分成3部分处理:
- Part 1:即为表格的最后一列,也就是所有的(p_i)的倍数。它们的积是({prod_{i=1}^t}(i*p_i)=t!*p_i^t)。由于n!中所有的(p_i)因子都应该被除去,所以我们只要递归计算(g(t))也就是(g({lfloor}{frac{n}{p_i}}{ floor}))。
- Part 2:表格左边的(p_i-1)列,可以每(p_i^{alpha_i-1})行分成一组。那么所有完好的s组构成Part 2。Part 2中的每一组的乘积,在模(p_i^{alpha_i})意义下都是相等的。所以Part 2的乘积就是第一组的s次方,即为(f(p_i^{alpha_i})^{{lfloor}{frac{n}{p_i^{alpha_i}}}{ floor}})。快速幂可求。
- Part 3:最后的残缺的一组。它的乘积在模(p_i^{alpha_i})意义下等于(f(n-s*p_i^{alpha_i})),也就是(f(n{mod p_i^{alpha_i}}))。
- (g(n) = Part1 * Part2 * Part3 {mod p_i^{alpha_i}})
递归终止的条件是n=0,此时返回值为1。
g(m),g(n-m)也用此法求出。
然后我们合并这6项,({ binom{n}{m}} {equiv} {p_i}^{v_{p_i}(n!)-v_{p_i}(m!)-v_{p_i}((n-m)!)}*{frac{g(n)}{g(m)g(n-m)}} {mod{p_i^{alpha_i}}})
(p_i)的幂部分使用快速幂,g(n)、g(m)、g(n-m)都与(p_i)互质,故可以逆元合并,最终得到(R_i)。
分析时间复杂度,瓶颈应在预处理上,为(O(sum_{i=1}^{k}{p_i^{alpha_i}})),当k=1,即p为素数幂时,可达(O(p))。其他部分皆在(log)或(log^2)级别。
代码
- 注:代码中的(r)数组对应题解中的(R_i) ,(P[i])表示题解中的(p_i^{alpha_i}),calc函数对应题解中的g。
#include<bits/stdc++.h>
using namespace std;
#define N 1000000
#define rg register
#define ll long long
namespace ModCalc{
inline void Inc(ll &x,ll y,ll mod){
x += y;if(x >= mod)x -= mod;
}
inline void Dec(ll &x,ll y,ll mod){
x -= y;if(x < 0)x += mod;
}
inline void Adjust(ll &x,ll mod){
x = (x % mod + mod) % mod;
}
inline ll Add(ll x,ll y,ll mod){
Inc(x,y,mod);return x;
}
inline ll Sub(ll x,ll y,ll mod){
Dec(x,y,mod);return x;
}
inline ll Check(ll x,ll mod){
Adjust(x,mod);return x;
}
}
using namespace ModCalc;
inline ll read(){
ll s = 0,ww = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')ww = -1;ch = getchar();}
while('0' <= ch && ch <= '9'){s = 10 * s + ch - '0';ch = getchar();}
return s * ww;
}
ll pn;
ll prime[100000+5];
bool isp[N+5];
inline void Eular(){
pn = 0;
for(rg ll i = 2;i <= N;i++)isp[i] = 1;
for(rg ll i = 2;i <= N;i++){
if(isp[i])prime[++pn] = i;
for(rg ll j = 1;i * prime[j] <= N;j++){
isp[i * prime[j]] = 0;
if(i % prime[j] == 0)break;
}
}
}
inline void exgcd(ll a,ll &x,ll b,ll &y){
if(!b){
x = 1,y = 0;
return;
}
exgcd(b,y,a%b,x);
y -= a / b * x;
}
inline ll power(ll a,ll n,ll mod){
ll s = 1,x = a;
while(n){
if(n & 1)s = s * x % mod;
x = x * x % mod;
n >>= 1;
}
return s;
}
inline ll inv(ll a,ll mod){
ll x,y;
exgcd(a,x,mod,y);
Adjust(x,mod);
return x;
}
ll k,m,n,mod;
ll p[20+5],P[20+5],r[20+5];
ll f[N+5];
inline ll calc(ll n,ll p,ll P){
if(!n)return 1;
ll part1 = calc(n / p,p,P);
ll part2 = power(f[P],n / P,P);
ll part3 = f[n%P];
return part1 * part2 % P * part3 % P;
}
inline ll C(ll n,ll m,ll p,ll P){
ll v = 0;
for(rg ll cur = n;cur;cur /= p)v += cur / p;
for(rg ll cur = m;cur;cur /= p)v -= cur / p;
for(rg ll cur = n - m;cur;cur /= p)v -= cur / p;
f[0] = 1;
for(rg ll i = 1;i <= P;i++){
f[i] = f[i-1];
if(i % p)f[i] = f[i] * i % P;
}
ll s1 = calc(n,p,P),s2 = calc(m,p,P),s3 = calc(n - m,p,P);
return power(p,v,P) * s1 % mod * inv(s2,P) % mod * inv(s3,P) % mod;
}
inline void exLucas(ll n,ll m,ll mod){
for(rg ll i = 1;i <= pn;i++){
if(mod % prime[i] == 0){
k++;
p[k] = prime[i],P[k] = 1;
while(mod % prime[i] == 0){
mod /= prime[i];
P[k] *= p[k];
}
}
if(mod == 1)break;
}
for(rg ll i = 1;i <= k;i++)r[i] = C(n,m,p[i],P[i]);
}
inline ll CRT(){
ll ans = 0;
for(rg ll i = 1;i <= k;i++)
Inc(ans,(mod/P[i]) * inv(mod/P[i],P[i]) % mod * r[i] % mod,mod);
return ans;
}
int main(){
n = read(),m = read(),mod = read();
Eular();
exLucas(n,m,mod);
cout << CRT() << endl;
return 0;
}