今天是钟皓曦老师的讲授~
合并石子拓展:
合并任意两堆石子,每次合并的代价是这两堆石子的重量的异或值,求合并成一堆的最小异或和。
状态设置:f [ s ] 把 s 所对应的石子合并的最小代价;

那么答案及就是:f [ 2n - 1 ];
最后一次操作还是将两堆石子合并成一堆,我们这里的合并方法怎么去找?
算 f [ s ] 的方法:去枚举 s 的所有子集,把子集和剩下的部分合并;

边界条件:将第 i 堆石子合并到第 i 堆石子的代价是 0;
for (int a=0;a<n;a++) //枚举每一位 f[1<<a] = 0; //只有这一位上的数字是1,意思就是将第a堆石子合并起来,代价显然是0
状态转移方程:
先枚举 s 的所有子集,考虑到子集是一定要比 s 小的:
1. 我们直接枚举一个小于 s 的数 i ,只有当 i 比 s 小的时候才有可能成为子集。
怎么判断 i 是 s 的子集?
s & a == a ;
s | a == s;
怎么判断剩下的元素?
b = s ^ a;
那么 f [ s ] = min ( f [ s ] , f [ a ] + f [ b ] + ( sum [ a ] ^ sum [ b ] ) );
#include<iostream> using namespace std; int main() { cin >> n; for (int a=0;a<n;a++) cin >> z[a]; for (int a=0;a<(1<<n);a++) //每种状态 for (int b=0;b<n;b++) if (a & (1<<b)) //如果当前这一位上有数,说明要合并第b堆石子 sum[a] += z[b]; //处理每种情况的石子重量之和 memset(f,0x3f,sizeof(f)); for (int a=0;a<n;a++) //枚举每一位 f[1<<a] = 0; //只有这一位上的数字是1,意思就是将第a堆石子合并起来,代价显然是0 for (int s=0;s<(1<<n);s++) //每种状态 for (int a=1;a<s;a++) //枚举s的所有子集,首先得保证小于s if ( (s|a) == s) //如果a是s的子集 f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s])); //s^a是剩下的集合 cout << f[(1<<n)-1] << endl;//最后的答案 return 0; }
时间复杂度:O(2n * 2n)= O(4n),显然过不了;
我们可以优化一下:
我们需要用更快的方法来枚举 s 的子集,发现如果我们只去枚举 s 的子集,就会变快很多,那么怎么写呢?
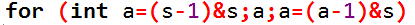
这句话就是枚举 s 的所有子集的标准写法,且只会枚举 s 的子集,因为和 s 进行与运算的话只会出来 s 的子集,再加上每次都减一再取子集,就能保证求出来的都是 s 的子集;
这样的话时间复杂度:O(3n);
#include<iostream> using namespace std; int main() { cin >> n; for (int a=0;a<n;a++) cin >> z[a]; for (int a=0;a<(1<<n);a++) //每种状态 for (int b=0;b<n;b++) if (a & (1<<b)) //如果当前这一位上有数,说明要合并第b堆石子 sum[a] += z[b]; //处理每种情况的石子重量之和 memset(f,0x3f,sizeof(f)); for (int a=0;a<n;a++) //枚举每一位 f[1<<a] = 0; //只有这一位上的数字是1,意思就是将第a堆石子合并起来,代价显然是0 for (int s=0;s<(1<<n);s++) //枚举每种状态 for (int a=(s-1)&s;a;a=(a-1)&s) //只枚举s的子集 f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s])); cout << f[(1<<n)-1] << endl;//最后的答案 return 0; }
博弈论动态规划
博弈论动态规划:一般是说,现在有个游戏 g,这个游戏一定是两个人玩,游戏特征是回合制且游戏没有平局(也就是说一定能分出胜负),分胜负的话一定是当某个人没办法再进行操作的时候他就输了;博弈论动态规划就是来解决这种问题的。

一个游戏有很多不同的状态。
我们可以采用一次操作可以把当前状态变到另一种状态。
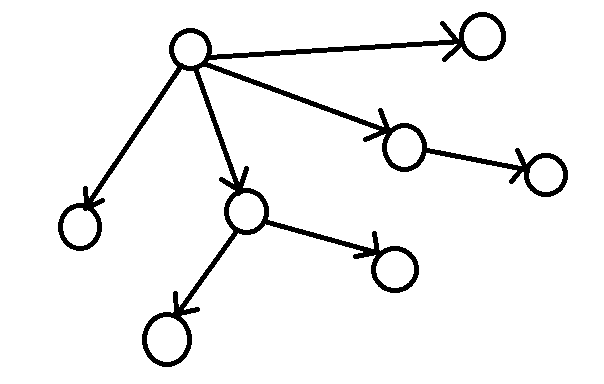
那么什么时候会输呢?当你在一个状态不能走到其他状态时你就输了,我们就把这个状态叫做必败态;
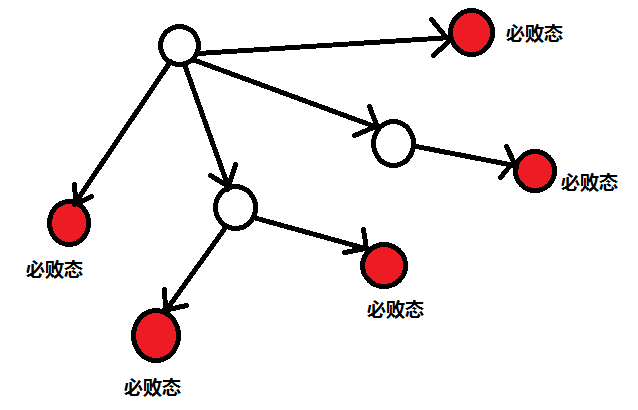
我们会发现所有可以通向必败态的状态叫做必胜态,因为我们从这个状态操作的话可以使对面走到必败态。

状态设置:我们用 f [ s ][ 0/1 ] 来表示游戏的一个状态,这个状态是否是必胜态还是必败态:0 是必败态,1 是必胜态;
状态转移方程:
有一个结点 s,如果能通向的所有状态有一个是必败态,这个点就是必胜态;否则的话如果通向的所有点都是必胜态,这个点就是必败态;


回归本题:
状态设置:f [ i ][ j ] 代表 s 还剩下 i 这么多,且对手上一轮减的数是 j 的情况下,是必胜还是必败;
状态转移方程:
枚举本回合要减的数 r,满足 1 <= r <= k * j,那么会转移到 f [ i-r ][ r ];
写博弈论DP的时候建议用记忆化搜索;
枚举一下一开始减去哪个数,然后记忆化搜索,枚举能达到的所有状态,只要能找到必败态就可以确定这个结点是必胜态了,如果不能找到则就是必败态;
递归终止条件:s 减到 0,就说明达到了必败态;
#include<iostream> using namespace std; bool f[1010000][20],g[1010000][20]; bool dfs(int i,int j) { if (i==0) return false; //如果被减到0了,就是必败态 if (g[i][j]) return f[i][j]; //记忆化 g[i][j]=true;f[i][j]=false; for (int r=1;r<=i && r<=k*j;r++) //枚举要减去的数 if (dfs(i-r,r) == false) f[i][j]=true; //如果减去这个数后达到必败态,那么当前的状态就是必胜态 return f[i][j]; } int main() { cin >> s >> k; for (int a=1;a<s;a++) //枚举一开始要减去哪个数 if (dfs(s-a,a) == false) //如果先手减去一个数后能达到必败态,那么先手必胜 { cout << "Alice" << endl; return 0; } cout << "Bob" << endl; //如果不能找到先手必胜的策略,则后手必胜 return 0; }
那如果我们有 n 个游戏呢?
我们的每次操作可以随便选择一个游戏去玩,如果一个人在每个游戏中都无法再移动的时候就输了;
经典的例子:取石子游戏
有 n 堆石子,每堆石子的石子数是 ai ,有两个人轮流取石子,每次可以取一堆石子的任意多石子,如果一个人没有石子取那就输了,问先手必胜还是必败;
状态设置: f [ b1 ][ b2 ][ b3 ]……[ bn ],表示第一堆石子还剩下 b1,第二堆石子还剩下 b2,……,第 n 堆石子还剩下 bn 时是必胜还是必败;
发现维数有点大,存不下,那只能换一种方法了;
介绍一下SG函数:
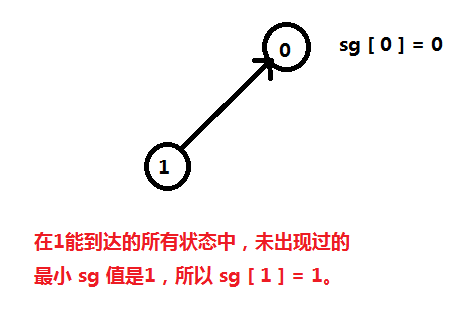
我们定义:sg [ i ] 表示从 i 能转移到的所有状态中没有出现过的最小自然数,且定义 sg [ 0 ] = 0;
如果一个游戏的 sg ≠ 0 的话,先手必胜;如果 sg = 0,先手必败;
我们找 1 能转化到的所有状态,将它们的 sg 写出来,再找最小的没有出现过的自然数:
我们找 2 能转化到的所有状态,将它们的 sg 写出来,再找最小的没有出现过的自然数:
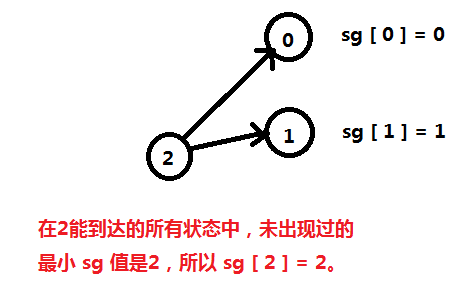
我们找 3 能转化到的所有状态,将它们的 sg 写出来,再找最小的没有出现过的自然数:

我们找 n 能转化到的所有状态,将它们的 sg 写出来,再找最小的没有出现过的自然数:
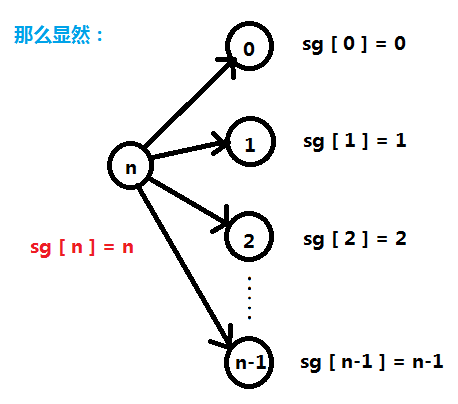
所以我们得出来一个规律:sg [ i ] = i;
因为 sg 函数是只对一个游戏来求的,但是我们要求的是 n 个游戏啊!
很重要的结论----SG定理:
n 个游戏的 sg 值等于每个游戏的 sg 值异或起来;
所以我们只需要求出每个游戏的 sg 值异或起来就好了;
由于这个题每堆石子的 sg 值就是这堆石子的石子数,所以我们只需要将每堆石子数异起来就好了。
代码十分简单呢:
#include<iostrean> using namespace std; int main() { cin >> n; int ans=0; for (int a=1;a<=n;a++) { int v; cin >> v; ans = ans ^v; //求出每个数的异或和,这个ans就是n个游戏的sg值 } if (ans!=0) cout << "Alice" << endl;//不为0,先手必胜 else cout << "Bob" << endl; //否则先手必败 }
拓展:
原先是可以取走任意多个石子,现在每次只能取走 1~4 个石子,问先手必胜还是必败;
sg [ 0 ] = 0;
sg [ 1 ] = 1;
sg [ 2 ] = 2;
sg [ 3 ] = 3;
sg [ 4 ] = 4;
由于一次最多取四个石子,所以 5 最多往前指 4 个,最多指到 1 而指不到 0,所以 5 的 sg 值是 0:
sg [ 5 ] = 0;
sg [ 6 ] = 1;
……
sg [ i ] = i % 5;
那么这个题不就做完了?
一般的做题思路:手算 sg 的规律,然后求出每个游戏的 sg 值,异或起来,判断是否为 0 就好了;

博弈论的一般做法:
把问题变得和取石子问题一模一样!
每次操作都可以看成是将奇数堆拿一个放在它左边的石子堆中。
只要当除了第一堆石子外,其他都是偶数堆的话这个人就输了。
所以奇数堆石子的下标就代表能移动多少距离;
我们把所有奇数堆的石子的下标取出来异或起来,如果是 0 则先手必败,否则先手必胜;

对手能从偶数编号搬到奇数编号上,那么我们就可以再将奇数编号搬到偶数编号上;
任何石子在偶数位置上就再也没用了,且如果奇数编号搬到偶数编号上也就没用了;
那就转化为将奇数位置上的石子搬到 0(不看偶数),问是否有先手必胜策略;
我们就转化成了取石子的游戏。
答案就是将所有奇数楼梯上的石子数异或起来,如果为 0 先手必败,否则先手必胜。

这个题和上一题是差不多的。
我们先求出每个格子距离右下角的曼哈顿距离,那么我们每次向右或向下移动,距离右下角的曼哈顿距离都是每次减小 1 的;
那么如果对手从偶数距离走到了一个奇数的距离,那么我们下一步就可以将它再走到偶数的距离,所以又转化成了上一个题。
距离终点的距离是奇数的棋子数量异或起来就是答案;

如果我们把它当成一个游戏来做,状压的话需要 22000 ,显然不行。
那么我们拆成多个游戏来做。
sg [ i ] 对于长度为 i 的横条,它的 sg 值是多少;
vector :n 能转移到的所有状态的 sg 值;
假设我们在这一个格子上涂了颜色:

那么这个格子周围的四个格子都不能涂颜色了(蓝色部分):

所以我们每一次操作就硬生生地将这一条长格子分成了两部分,我们可以将这两部分看作是两个重新开始的游戏。
所以 sg [ n ] = sg [ a - 3 ] ^ sg [ n - a - 2 ] ;
然后我们再递归求左边和右边就好了。
#include<iostream> #include<algorithm> #include<vector> using namespace std; int dfs(int n) { if (n==0) return 0; if (f[n]) return sg[n]; //记忆化 f[n]=true; vector<int> z; for (int a=1;a<=n;a++) { int l = max(a-3,0); //左边的游戏长度 int r = max(n-a-2,0); //右边的游戏长度 z.push_back( dfs(l) ^ dfs(r) ); } sort(z.begin(),z.end()); z.push_back(233333333); //防止栈溢出 for (int a=0,p=0;;a++) { if (z[p] != a) { sg[n] = a; return sg[n]; } while (z[p]==a) p++; } } int main() { cin >> n; if (dfs(n)) cout << "Alice" << endl; else cout << "Bob" << endl; }

状态设置:f [ x ][ y ] (x,y)这个状态是必胜还是必败;
但是 30000 * 30000 的空间显然会爆。
考虑到 x 每次变换成原来的两倍,要么是原来的三倍,那么就可以表示成 2a * 3b 的形式;
改成:f [ a ][ b ][ y ] 表示(2a * 3b ,y)这个状态是必胜还是必败;
下午悲催考试分析


第一道题比较水,唯一的坑点就是求最小公倍数相乘的时候可能会爆 int,其他的也没什么好说的。
具体求 gcd 的方法:扩展欧几里得;
具体求 lcm 的方法:两数相乘再除以 gcd(就是这里乘的时候会爆 int);
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } long long a,b,gc,lcm; //注意开long long long long gcd(long long x,long long y) //扩展欧几里得求最大公约数 { if(y==0) return x; else return gcd(y,x%y); } int main() { //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); a=read(); b=read(); gc=gcd(a,b); //最大公约数 lcm=a*b/gc; //求最小公倍数 printf("%lld",gc^lcm); //异或起来就是答案 return 0; }



考场上许多大佬想到了之前学的强连通分量,然后就用了缩点+DP,表示我太蒟了没有想到,直接一遍 dfs 拿到 80 pts。
考虑这个题最优的路径实际上不只一种:
假设我们已经找到了一个使得(最大值 - 最小值)最大的一条路径:

考虑到最大的点前面,最小的点后面再走路径的话是完全可以的,对答案是没有影响的:

我们要求的就是找出从最大点走到最小点或者从最小点走到最大点两种路径的答案;
所以我们可以考虑算这么一个东西:
枚举每一个点,将当前点看作是最大值的话,是不是要找能到的所有路径中的最小值?
但是不知道这个最小值是在当前点上方还是下方(如果是在上面的话,就是从最小值走到了最大值;如果在下面的话,就是从最大值走到了最小值),所以我们要向上向下各走一边找个最小值:
1.每个点向后走;
2.每个点向前走;
从每个点出发,能走到的所有点当中最小的是多少,以及从这个点向回走的最小值:
我们有一种暴力方法:枚举每个点作为起点或终点,直接去枚举max是哪个点。
怎么求这个点向后走的最小值,直接 dfs 就好了;期望得分80 pts;
100 pts:
每次都要 bfs 是我们这个算法慢的原因,考虑到我们正着算第一个点的答案和反着第二个点的答案不会对答案造成影响;
我们可以按照每个点的点权从小到大排序,然后一个点一个点地处理答案,和刚刚处理有什么区别?
这样我们 bfs 的时候就不用再去求最小值了;
只需要对每个点我们只要遇到已经算出答案的点就停了;
每个点只被算过一次,所以时间复杂度是线性的;
时间复杂度:O(n+m);



数据范围这些小,所以应该是用状压DP做!
状态定义:f [ s ] s 所对应的人之间,能不能通过交换变得合法;
发现我们只需要排序就好了,看看相邻的两两间相差是否小于 c;
最坏的情况:n-1 次;
我们找到 c1 这把刷子,如果正好又拿着 c2 这把刷子的话就不用换了,如果不是拿着 c2 这把刷子,那就换过来,这样的话我们就可以通过一次操作搞定第一个人;
每次交换一定能搞定一个人;
最后一次交换能搞定两人,所以所需要的次数最多为 n-1;
那么什么时候答案小于 n-1?
如果一个人拿的刷子本来就合法,那就不用换了;
g [ s ] 我要让 s 这一堆人合法所需要的最小步数;
如果 s 内部能够自己解决,那么 g [ s ] 最大就是 k-1;
我们需要找比 k 更小的数;
看到数据最多是 16,这告诉我们 3n 也是可行的,我们应该去枚举子集:
如果我们能将一个状态 s 分成 n/2
问题转化成:最多能将 n 个人分成多少个部分,使得他们内部都能通过换刷子来解决问题;
如果我们能将 n 分成 k 部分,答案就是 n - k;
重新定义状态:g [ s ] 我最多将 s 分成多少个部分使其能自己解决;
枚举 s 的所有子集,求出子集和剩下的部分能分成多少个部分取个max;
答案就是: n - g [ 2n - 1 ];



与之前线段树不同的是:区间加上个斐波那契数列,区间求和。
两个斐波那契数列的和仍然是个伪斐波那契数列;
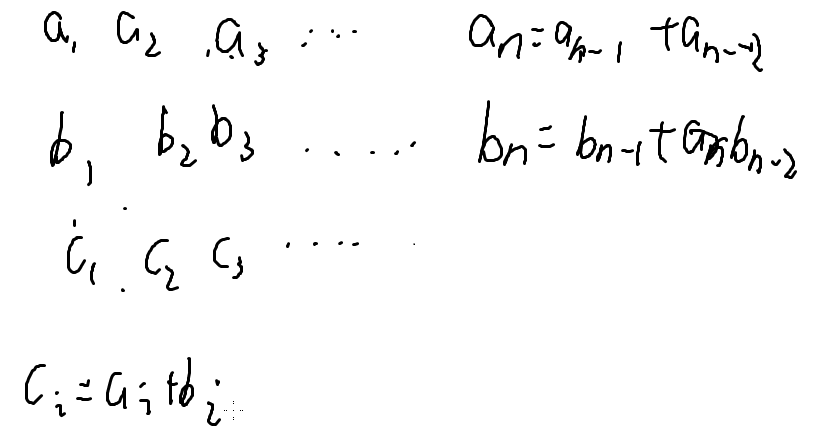
打标记的时候只需要求前两个数加了多少就好了。
所以我们线段树上要记上两个东西:给第一个数加上c1,给第二个数加上c2;
这段区间的和会怎么变?
之和三个值有关:c1,c2,这段区间的长度;
可以预处理一个数组:第 i 项等于多少倍的c1加上多少倍的 c2;
顺便还可以求个前缀和。