看到Day 2的题真的想打死zay了,忒难了QwQ~
T1 江城唱晚

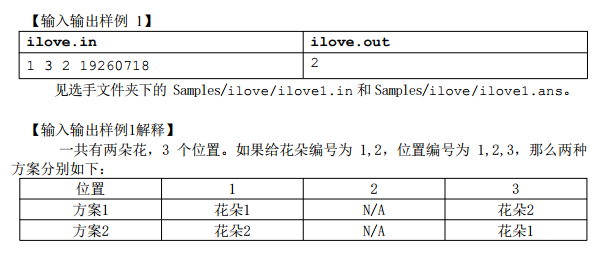
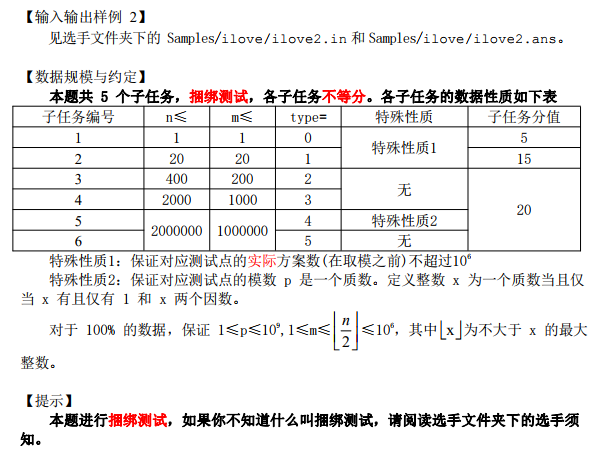
这明显是个求方案数的计数问题,一般的套路是DP和组合数学。
正如题目中所说,这个题是一个 math 题。 ----zay不会的 math 题让我们做?QwQ


DP已经优化到了尽头,现在我们考虑组合数学!
zhx:这应该是个小学奥数题!
恩,这其实就是个经典的组合数问题啦。
首先我们以数学的来思考这个题:
我们有n个位置来摆放m盆花,还要保证每盆花之间至少有一个空位置。如果我们单单去刻意拆空位置的话,我们会发现这很难实现,那怎么简单得去保证每两盆花之间有空位置呢?
回忆起了当时做这种题的思路:先让每盆花之间插一个空位置!
什么意思呢?
就像这样,我们先让m盆花之间每盆花都相隔一个空位置(下划线_ 代表的是空位置):

这样我们就预先将m盆花放好了,还占了(m-1)个空位置,So我们还有 n - m - (m -1 )=n - 2 * m +1 个空位置;
所以我们接着将这 n - 2 * m + 1 个空位置随便往里边差不就能产生所有的情况了嘛?
只不过要注意我们是将 (n - 2 * m + 1)个空位置往(m + 1)个空里插,求方案数!因为注意到第1盆花左边和第m盆花右边也可以插入空位置。
然后我们再看一个公式:
将x个球放进y个盒子里的方案数:
球同,盒不同,盒可以为空 C(x+y-1, y-1)
解释一下为什么是这样:
看到我们的原问题:将(n - 2 * m + 1)个空位置往(m + 1)个空里边插,就可以抽象的看成:将(n - 2 * m + 1)个小球放进(m + 1)个盒子里,然后求方案数;
其中每一个空位置是一样的,但是插到哪个空却是不同的,并且每两盆花之间可以不再插空位置(因为之前我们已经在每两盆花之间插了一个空位置,所以这时候这两盆花的空位置数就是1)
至于为什么公式是这样……,找度娘鸭QwQ~!
显然对于这个题,x = n - 2 * m + 1,y = m + 1,我们代入公式就是:C(n - m + 1,m); // C的下标对应的是括号左部分,C的上标对应的是括号右部分
再找度娘找到了求组合数的公式:
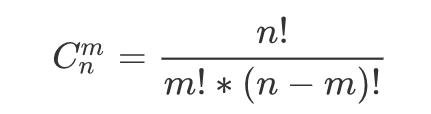
那么:
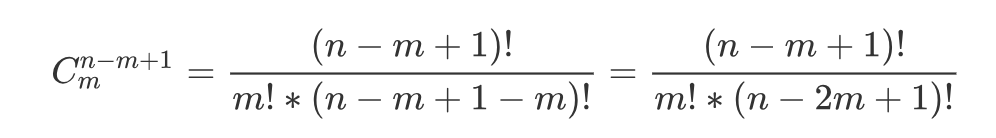
因为花盆的编号不同也算是不同的方案,而所有花的编号的不同方案数是 ![]() ,所以我们将这两部分乘起来就是答案!
,所以我们将这两部分乘起来就是答案!
细心的同学会发现正好可以将m!约掉,所以最后的答案就是:
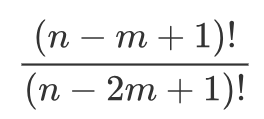
其实这里求最后答案也是有技巧滴(好像只能这么求吧),我们知道x!是从1乘到 x,那么对于这两个阶乘是有公共部分的!
∵ n - m + 1 > n - 2 * m + 1
∴(n - m + 1)!包含(n - 2 * m + 1)!,即(n - 2 * m + 1)! | (n - m + 1)!
∴ (n - m + 1)!
= 1 * 2 * 3 * …… * (n - 2 * m + 1)* (n - 2 * m + 2)* …… *(n - m)*(n - m + 1)
=(n - 2 * m + 1)!*(n - 2 * m + 2)* …… * (n - m)*(n - m + 1)
∴(n - m + 1)!/(n - 2 * m + 1)!=(n - 2 * m + 2)*(n - 2 * m + 3)* …… *(n - m)*(n - m + 1)
最后注意一下乘的过程中不断取模,防止爆long long ;
代码如下:
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int type,n,m,maxn; long long x,y,mod; long long jc[5000001]; int main() { freopen("ilove.in","r",stdin); freopen("ilove.out","w",stdout); type=read();n=read();m=read();mod=read(); //从n个位置里摆m盆花 if(n<2*m-1) //如果n<2*m-1,就不能预先摆好m盆花并且每盆花之间有一个空位置 { cout<<0; //0种方案 return 0; } jc[1]=1; maxn=max(n,n+m-1); for(int i=2;i<=maxn;i++) jc[i]=jc[i-1]%mod*i%mod; //求出了1~m的阶乘 if(n==2*m-1) //这时候每盆花之间只可能有一个空位置,那么方案数就是m! { printf("%lld",jc[m]); return 0; } long long ans=1; //怕爆int for(int i=n-2*m+2;i<=n-m+1;i++) ans=ans*i%mod; printf("%lld",ans); return 0; }
一些好像是好像又不是题外话的话:
身为蒟蒻的我当然也推出来了这个公式啦,但是我当时没考虑到有公共部分,我是直接两部分的阶乘相除;按理来说没错是吧(我一开始也不知道自己到底是哪错了,直到jyy大佬给我讲了之后才明白,哎,果然我还是太菜了),但是我却忽略掉最重要的一点:模意义下不能做除法!导致最后输出都是0。
(⊙o⊙)…其实我当时也想到这一点啦,就想方设法求(n - 2 * m + 1)!的逆元:线性?爆空间!费马小定理?不互质也不会求欧拉函数,还可能也爆空间!扩展欧几里得?这个应该可以!QwQ~
然后就写上了扩展欧几里得算法,当时的确忘了怎么写给写炸了,但回头我再改了改,还是有好多点过不去(好像只有当模数是质数的时候才能过去QwQ)
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int type,n,m,maxn; long long x,y,mod; long long jc[5000001]; int exgcd(long long a,long long b,long long &x,long long &y) { if(b==0) { x=1;y=0;return a; } exgcd(b,a%b,x,y); int r=x; x=y; y=r-(a/b)*x; } int main() { freopen("ilove.in","r",stdin); freopen("ilove.out","w",stdout); type=read();n=read();m=read();mod=read(); //从n个位置里摆m盆花 if(n<2*m-1) { cout<<0; return 0; } jc[1]=1; maxn=max(n,n+m-1); for(int i=2;i<=maxn;i++) jc[i]=jc[i-1]%mod*i%mod; //求出了1~m的阶乘 if(n==2*m-1) { printf("%lld",jc[m]); return 0; } int gcd=exgcd(jc[n-2*m+1],mod,x,y); x=(x%mod+mod)%mod; printf("%lld",jc[n-m+1]*gcd%mod*x%mod); return 0; }
T2 不老梦


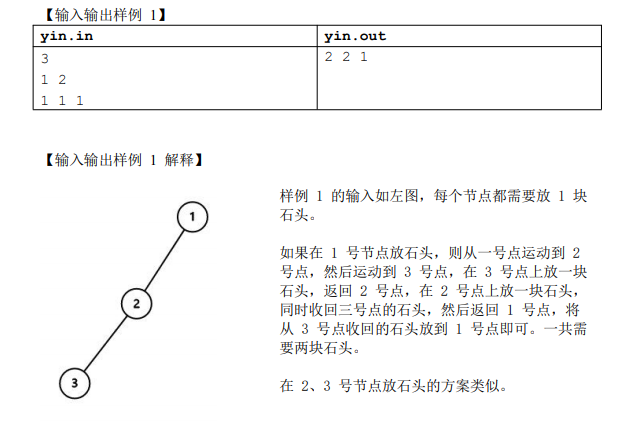
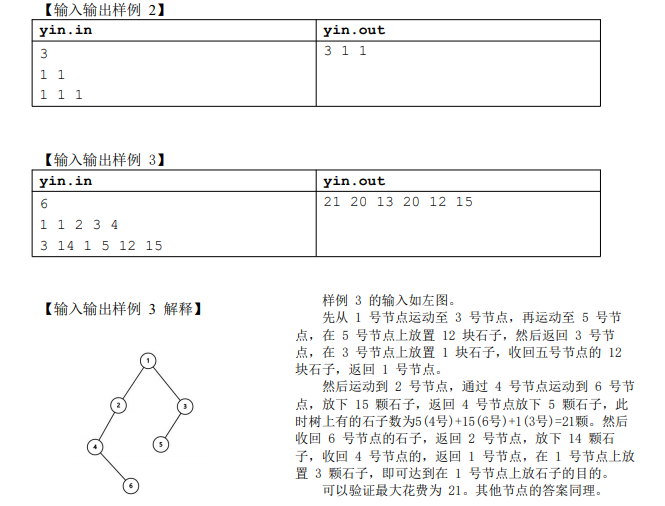
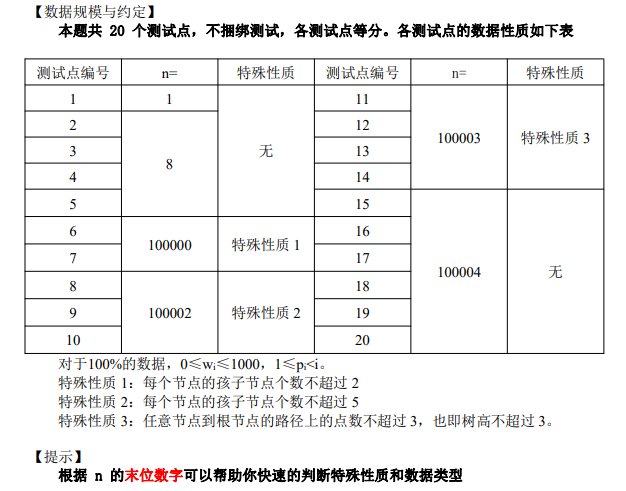
测试点 1: 显然直接输出 w1 即可。期望得分 5 分。
测试点 2-5: 爆搜,搜出一个放石子的顺序,然后 O(n) 的 check 是否合法。时间复杂度 O(n!*n)。期望得分 20 分。
测试点 6-7: 注意到根据题目规定的走法,在进入一个节点以后,必须遍历完它的整个子树, 否则一旦离开这个节点,再也无法进入这棵子树,从而导致该节点的某个孩子没能放 上石子,导致这个节点不能放上石子。同时又有每个节点放上石子以后,它的子树的 石子可以全部取回。设在节点 u 放石子需要有 ansu 个石子(ansu=(∑ansk)+wu,k是u的所有孩子),则放完 u 以后可以取回 ansu-wu 个石子。 于是考虑影响问题答案的显然是从 u 进入每个孩子的顺序,由于最多有两个孩 子,直接比较一下就可以知道先进入哪个孩子更优秀了。时间复杂度 O(n),期望得分 10 分。
测试点 8-10: 延续上一组测试点的思路,由于只有最多 5 个孩子,可以直接爆搜选孩子的顺序,看看哪个更优秀。时间复杂度 O(n*x!),其中 x=5。期望得分 15 分。
测试点11-14:由于树高最多三层是吧,那么因为第三层放了之后不能取回石子,所有先放谁无所谓的,关键就是从根结点1出发看看先遍历第二层的哪个儿子结点了;
考虑走完节点 u 的所有孩子 v 所需要的总石子数 cu,显然是越少越好。证明如下:

那么问题变成了: 有 x 个商品,购买第 i 个物品需要手里有 ansi 元钱,花费 wi 元。求一个顺序 使得购买所有商品所需要的钱数最少。
这个问题的最最优顺序是按照 ansi-wi 不升序购买,也就是差值越大越要先买。 考虑证明:
设有两个物品 i,j,设 ai=ansi-wi,aj=ansj-wj。且 ai>aj。
考虑先买 i 再买 j 的 花费是多少:
我们买 i 需要ansi;到了买j的时候我们已经取回了ai颗石子(为了少用石子是一定要收回这些石子的),那么我们尽量要用这 ai 颗石子去买 j;考虑到买 j要用ansj,如果ansj<ai,那么我们就不用再花更多的石子了,那么总的花费就是ansi;如果ansj>ai,那么我们还需要添上(ansj-ai)才行,又因为ai=ansi-wi,所以我们要添上(ansj-ansi+wi)才可以买到 j,加上我们一开始买 i 所需要的ansi,那么一共要(ansj - ansi+wi)+ansi=ansj+wi,而我们并不知道ansj 与ai 的大小关系,所以我们用一个max来表示最多需要花费的石子,那么得出式子: max(ansi, wi+ansj) ①;
同理先买 j 的花费是 max(ansj, wj+ansi) ②。
因为 ai=ansi-wi,aj=ansj-wj ,则ansi =ai + wi ,ansj =aj + wj,代入原式提出 w,则 ①=wi+max(ai,ansj),②=wj+max(aj,ansi)=wj+max(aj,ai+wi)=wj+ai+wi。 考虑 ① 式的 max 如果取前面一项,则 ①=wi+ai<②,如果取后面一项则 ① =wi+ansj=wi+aj+wj<②,于是无论怎么取,①式恒小于②式,于是先买 i 更优。数学归纳可得按照 ansi-wi 不升序购买最优。
于是按照这个顺序,排一遍序即可。期望得分 20 分。
测试点 15-20: 可以发现上面的结论同样适用于树高更高的情况,于是在 dfs 回溯的时候对子节 点排序,即可算出该节点的答案,期望得分 30 分。
标程代码:
#include <cstdio> #include <vector> #include <algorithm> const int maxn = 100010; int n; int MU[maxn], ans[maxn]; std::vector<int>son[maxn]; void dfs(const int u); bool cmp(const int &_a, const int &_b); int main() { freopen("yin.in", "r", stdin); freopen("yin.out", "w", stdout); scanf("%d", &n); for (int i = 2, x; i <= n; ++i) { scanf("%d", &x); son[x].push_back(i); } for (int i = 1; i <= n; ++i) { scanf("%d", MU + i); } dfs(1); for (int i = 1; i < n; ++i) { printf("%d ", ans[i]); } printf("%d ", ans[n]); return 0; } void dfs(const int u) { for (auto v : son[u]) { dfs(v); } std::sort(son[u].begin(), son[u].end(), cmp); int _ret = 0; for (auto v : son[u]) { if (_ret >= ans[v]) { _ret -= ans[v]; } else { ans[u] += ans[v] - _ret; _ret = ans[v] - MU[v]; } } ans[u] += std::max(0, MU[u] - _ret); } inline bool cmp(const int &_a, const int &_b) { return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]); }