一、行列式
行列式的概念
概念：数 不同行不同列元素乘积的代数和
二阶行列式的计算方法：
三阶行列式的计算方法：
排列：由1，2...，n组成的有序数组称为一个n阶排列，通常用j1，j2 ，...jn表示n阶排列。
逆序：一个排列中，如果一个大的数排列在一个小的数的前面，就称这两个数构成一个逆序。
逆序数：一个排列的逆序的总数称为这个排列的逆序数。
如果一个排列的逆序数是偶数，则称这个排列是偶排列，否则称为奇排列。
n阶行列式：不同行不同列的n个元素的乘积的代数和。
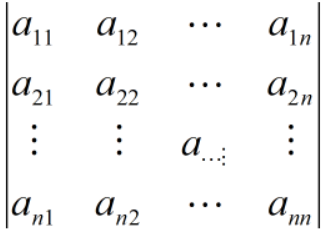
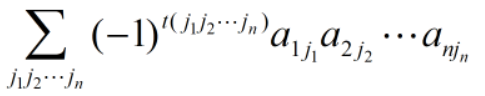
当j1，j2 ，...jn是偶排列时，该项前面带正号，当j1，j2 ，...jn 时奇排列时，该项前面带负号。
上三角以及下三角行列式的计算方法：
行列式的性质
1、经转置行列式值不变
2、某行有公因数k可把k提出
特别地，若某行元素全为0，则D=0
3、两行互换行列式的值变号
特别地，两行相同=>D=0两行成比例=>D=0
4、某行所有元素都是两个数的和，则可把行列式写成两个行列式之和
5、某行的k倍加到另一行，行列式的值不变
注意：1.不要与矩阵初等变换相混。
2、不要与矩阵运算相混
展开公式
行列式按行（列）展开公式：
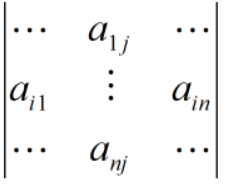
余子式： Mij
代数余子式：Aij=(-1)i+jMij
展开公式
1、按行按列展开：
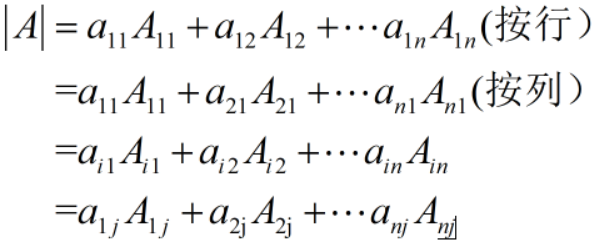
2、某一行的所有元素与另一行相应元素的代数余子式乘积之和等于0。
重要公式：
1、主对角线上下三角：a11a22...ann
2、副对角线上下三角：（-1）n(n-1)/2a1na2 n-1...an1
3、
4、
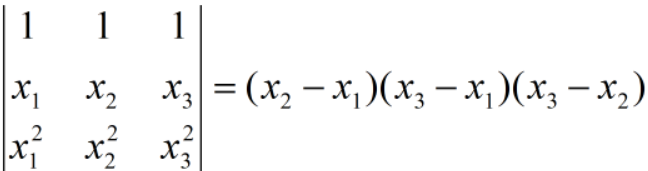
克拉默法则：
如果系列行列式D=|A|≠0，则方程组有唯一解，且：
其中Di=
推论1，若齐次方程组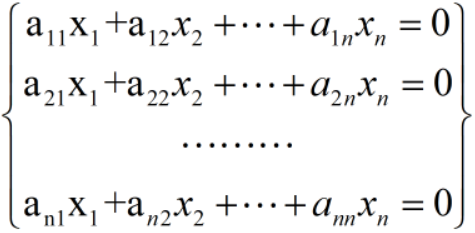
的系数行列式不为0，则方程组只有一组零解x1=0，x2=0，...，xn=0。
推论2，若齐次方程组（2）有非零解，则它的系数行列式必为0.
强化阶段
1、 数字型（展开公式）
把第1行的k倍加到某i行
把每一行都加到第1行
逐行相加
2、证明题用到归纳法时
当只与一项有关系时，用方法①，当与两项有关系时，用方法②。
①1、验证n=1时，命题正确
2、设n=k时，命题正确
3、证明n=k+1时，命题正确
4、得证
②1、验证n=1，n=2命题正确
2、设n<k命题正确
3、证明n=k命题正确
4、得证
3、抽象型
行列式性质恒等变形
矩阵公式，法则恒等变形，E恒等变形
特征值，相似
注意：
4、应用
特征多项式，A*,A-1,相关，无关，正定，克拉默法则。
5、证|A|=0
Ax=0有非零解
反证法 用A-1找矛盾
r(A)<n
0是特征值 |A|=∏λi
|A|=-|A|
二、矩阵
概念、运算（乘法）
m✖n个数排列成如下m行n列的一个表格：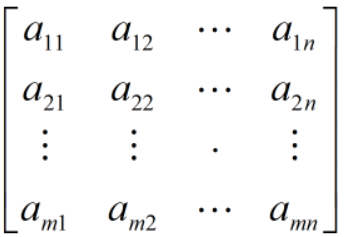
称为是一个m✖n矩阵，当m=n时，称为n阶矩阵或n阶方阵，简记A。
如果一个矩阵的阶所有元素都是0，即
称这个矩阵为零矩阵，简记0.
如A和B都是m✖n矩阵，称A和B是同型矩阵，设A和B都是m✖n矩阵，如
称矩阵A和B相等，记A=B。
设A为n阶矩阵，其所有元素构成的行列式，称为方阵A的行列式，记为|A|。
注意：1、仅方阵才有行列式|A|。
2、A=0与|A|=0不要混。
矩阵的加法（其中A，B都为m✖n阶矩阵）：
数与矩阵相乘：数k与矩阵A的乘积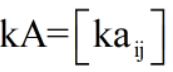
运算法则：
加法：A，B，C同型
A+B=B+A
(A+B)+C=A+(B+C)=A+B+C
A+0=0+A=A
A+(-A)=0
数乘运算：
k(mA)=m(kA)=(mk)A
(k+m)A=kA+mA
k(A+B)=kA+kB
1A=A,0A=0
乘法运算：
A——m✖s，B——s✖n
AB=C——m✖n
ai1b1j+ai2b2j+...+aisbsj=Cij
注意：
1、AB≠BA
2、由AB=0不能推出A=0或B=0
3、由AB=AC且A≠0不能推出B=C
单位矩阵E：
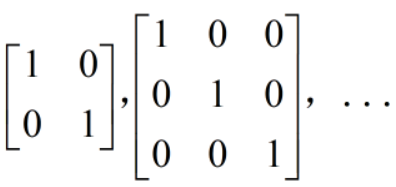
运算法则：
（AB)C=A(BC)=ABC
A(B+C)=AB+AC
(A+B)C=AC+BC
AE=A,EA=A
A——n阶：A.A=A2
A.A...A(k个A相乘)=Ak
转置：将A矩阵的行列互换得到的新矩阵称为A的转置矩阵，记为AT
运算法则：
（A+B）T=AT+BT
(kA)T=kAT
(AB)T=BTAT
(AT)T=A
定理（行列式乘法公式）：设A，B都是n阶矩阵，则|AB|=|A|.|B|
伴随矩阵，可逆矩阵
A-n阶矩阵，行列式|A|所有的代数余子式Aij所构成的如下矩阵：
主对角线互换，副对角线变号。
伴随矩阵的公式：AA*=A*A=|A|E
(kA)*=kn-1A*
|A*|=|A|n-1
（A*)*=|A|n-2A
（A*）-1=（A-1）*=A/|A|
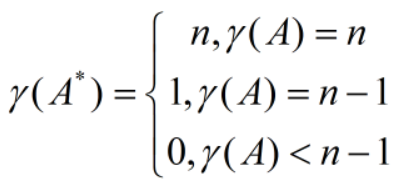
可逆矩阵：对于n阶矩阵A，如果存在n阶矩阵B，使AB=BA=E则称矩阵A是可逆的，称B是A的逆矩阵。
命题：如矩阵A是可逆的，那么A的逆矩阵是唯一的，记作A-1
定理：A可逆<=>|A|≠0
推论：A，B是n阶矩阵，如AB=E，则A-1=B
逆矩阵的公式法则：
1、如A可逆，则A-1也可逆，且（A-1)-1=A
2、如A可逆，且k≠0，则kA可逆，且（kA）-1=A-1/k
3、如A，B均可逆，则AB也可逆，且（AB）-1=B-1A-1 特别的（A2）-1=(A-1)2,(An)-1=(A-1)n
4、如A可逆，则AT也可逆，且（AT)-1=(A-1)T
注意：
1、如A可逆，则|A-1|=1/|A|
2、当A,B,A+B都可逆时，一般（A+B）-1≠A-1+B-1
求逆：
1、定义法 AB=E
2、用伴随 A-1=A*/|A|
3、初等行变换：
4、分块：
对角矩阵：
注意：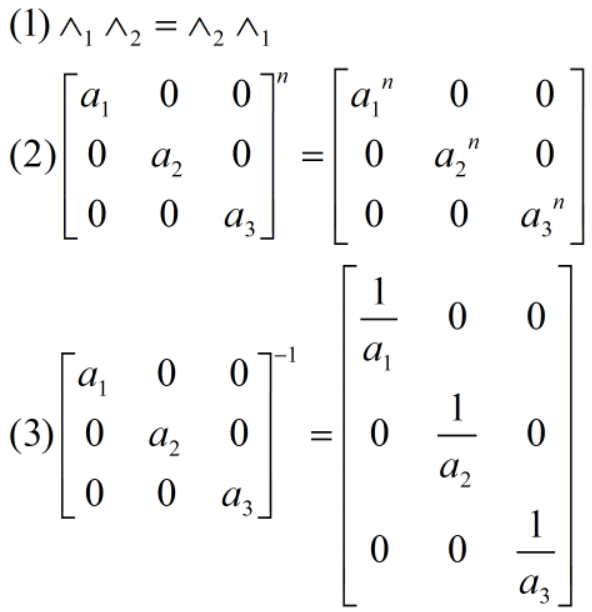
初等变换，初等矩阵
矩阵的初等变换：
1、用非0常数k乘A某行的每个元素
2、互换A中两行元素的位置
3、把A中某行所有元素的k倍加到另一行对应的元上
初等矩阵：
单位矩阵经过一次初等变换所得到的矩阵称为初等矩阵。
关键点：
初等矩阵P左乘矩阵A，其乘积PA就是矩阵A作一次与P同样的行变换。
初等矩阵P右乘矩阵A，其乘积AP就是矩阵A作一次与P同样的列变换。
初等矩阵的逆：均可逆，且其逆是同类型的初等矩阵。
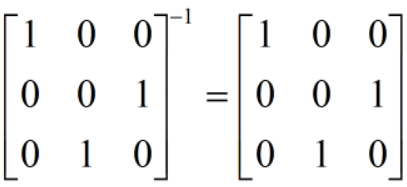
行阶梯矩阵：
1、如果有零行，则零行在矩阵的底部。
2、每个非零行的主元（即该行最左边的第1个非0元）所在列下面元素都是0。
行最简：
一个行阶梯矩阵，如果还满足：非零行的主元都是1，且主元阶在列的其他元素都是0
重要结论：
A可逆=A可表示为若干初等矩阵的乘积。
分块矩阵
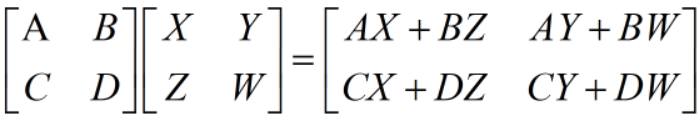
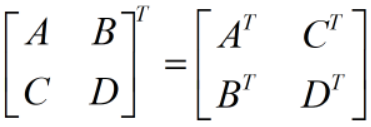
设A，B分别是m阶，n阶，则有：
若A为m✖n阶矩阵，B为n✖s阶矩阵，则：AB=A（b1b2...bs)=（Ab1,Ab2...,Abs)
方阵的行列式
1、|AT|=|A|
2、|kA|=kn|A|
3、|AB|=|A|.|B| |A2|=|A|2
4、|A*|=|A|n-1
5、|A-1|=1/|A|
6、
秩（矩阵）
1、k阶子式：A-m✖n，任取k行与k列（k<=m,k<=n)位于交叉点的k2元素，按A中的位置次序而得到的k阶行列式，称为矩阵A的k阶子式。
2、矩阵的秩：A-m×n，如存在r阶子式D≠0，且所有r+1阶子式（如存在）全为0，则称矩阵A的秩为r，记作r（A）=r。并规定零矩阵的秩为0.
定理：经初等变换矩阵的秩不变。
r（A）=A的列向量秩=A的行向量的秩
r（A）=r<=>A中存在r阶子式不为0，而每一个r+1阶（如果有）子式全为0.
r（A）>=1<=>A≠0
矩阵秩的公式：
1、r（AT）=r（A）
2、r（kA）=r（A）k≠0
r（0E-A）=r（A)
r（A-E）=r（E-A）
3、r（A+B）<=r（A）+r（B）
4、r（AB）<=min（r（A），r（B））
若A可逆
r（AB）=r（B），r（BA）=r（B）
5、r（ATA）=r（A）
6、A——m✖n，B——n✖s且AB=0，则r（A）+r（B）<=n
7、
若A~B ，则r（A）=r（B）
r（A+kE）=r（B+kE）
正交矩阵
A-n阶，满足AAT=ATA=E，称A为正交矩阵。
（1）A是正交矩阵<=>AT=A-1
（2）A是正交矩阵=>|A|=1或-1
（3）内积
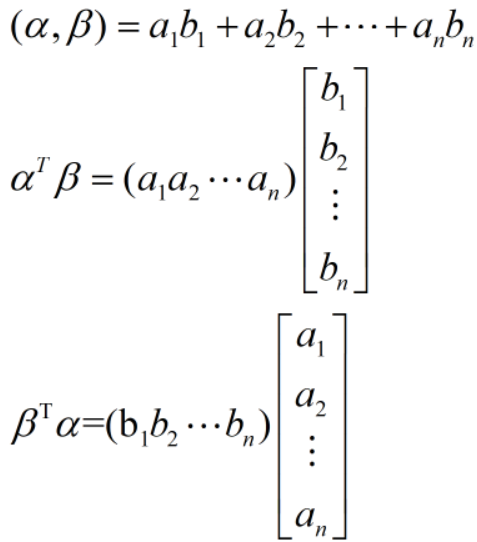
如（α，β）=0称α与β正交
强化阶段
一、概念，运算
乘法
αβT，βαT，ααT，βTα，αTβ，αTα
分块
求An
（1）如r（A）=1，有A=αβT =>A2=(αβT)(αβT)=α(βTα)βT=λA,λ=βTα∑aii 迹 An =λn-1A
（2）
二、伴随矩阵，可逆矩阵
AA*=A*A=|A|E 求逆，证可逆
求A*的方法
（1）直接法：用定义 不要丢+，-号，不要排错队
（2）间接法：A*=|A|A-1
三、初等变换，初等矩阵
四、矩阵的秩
行列式，相关，无关，方程组的解。
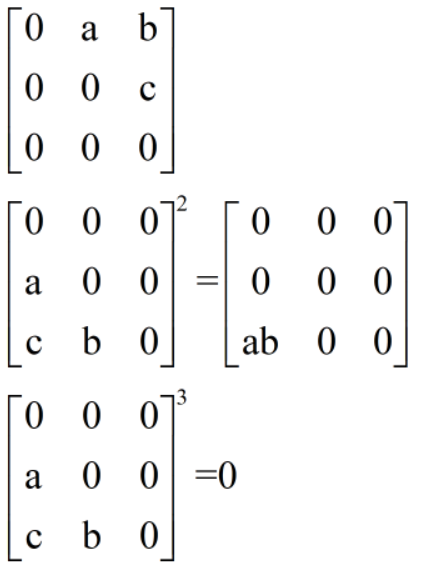
五、当秩为1时，有如下结论：
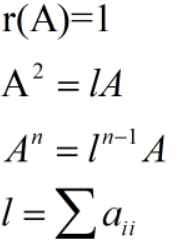
三、向量
概念，运算
n维向量：n个数a1,a2,...,an构成的有序数组称为n维向量。
ai称为向量的第i个分量（i=1，2，...，n)
如果向量的所有分量都是0，就称其为零向量，记作0=（0，0，...，0）T
设n维向量：
加法与数乘满足：
线性表示
定义：m个n维向量α1，α2，...，αm，及m个实数k1，k2，...，km。称：k1α1+k2α2+...+kmαm是向量α1，α2，...，αm 的一个线性组合，k1，k2，...，km称为这个线性组合的系数。
定义：如果向量β能表示为α1，α2，...，αm的线性组合，即存在一组数k1，k2，...，km使β=k1α1+k2α2+...+kmαm则称向量β可以由α1，α2，...，αm线性表出（示）。
定理：向量β可以由α1，α2，...，αm线性表示<=>任意实数k1，k2，...，km 使k1α1+k2α2+...+kmαm=β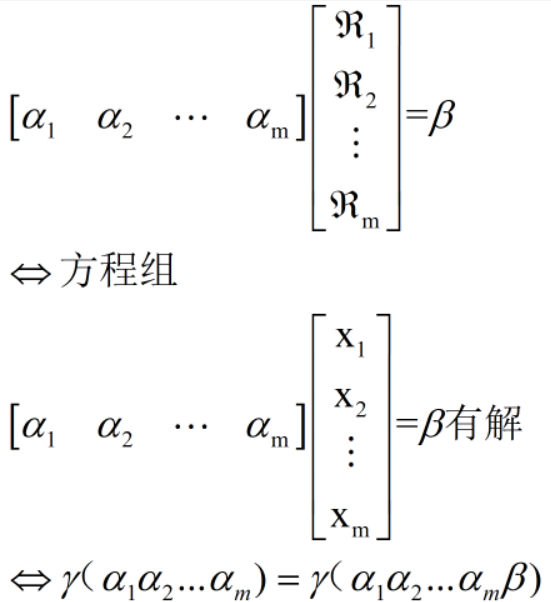
已知α，β1，β2，β3，γ1，γ2是n维向量，若α可由β1，β2，β3 线性表示，β1，β2，β3 可由γ1，γ2 线性表示，则α可由γ1，γ2 线性表示。
定义：设向量组（Ⅰ）α1，α2，...，αs；（Ⅱ）β1，β2，...，βt；若（Ⅰ）中每一个向量αi（i=1，2，...，s）均可由（Ⅱ）线性表示，则称向量组（Ⅰ）可由向量组（Ⅱ）线性表示。若向量组（Ⅰ）和（Ⅱ）可以互相线性表示，则称向量组（Ⅰ）和(Ⅱ）等价。
相关、无关
定义：对m个n维向量α1，α2，...，αm ，若存在不全为0的实数k1，k2，...，km 使k1α1+k2α2+...+kmαm=0成立，则称向量组α1，α2，...，αm 线性相关，否则称其线性无关。
定理：n维向量α1，α2，...，αm 线性相关
<=>存在不全为0的k1，k2，...，km 是k1α1+k2α2+...+kmαm=0
<=>存在不全为0的k1，k2，...，km 使
<=>齐次方程组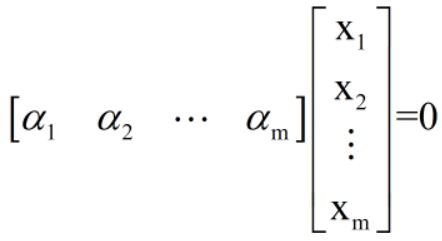
有非0解
<=>γ（α1，α2 ，...，αn ）<m
推论：
1、n个n维向量α1，α2，...，αn 相关<=>|α1，α2，...，αn |=0。
2、n+1个n维向量必线性相关。
α 相关<=>α=0
α1，α2相关<=>α1，α2 共线
α1，α2 ，α3相关<=>α1，α2 ，α3 共面
推论3：如α1，α2 ，...，αs 线性相关，则α1，α2 ，...，αs ，...,αt必线性相关
推论4：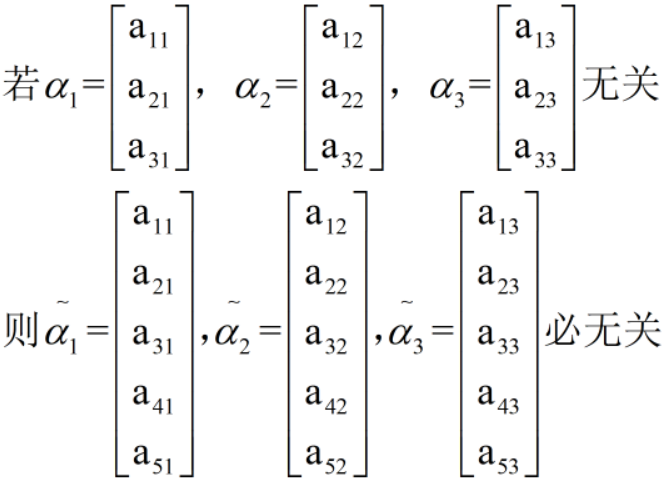
定理：向量组α1，α2 ，...，αs （s>=2)线性相关<=>至少有一个向量αi可由其余向量α1，...αi-1 ，αi+1...，αs 线性表出。
定理：如n维向量α1，α2 ，...，αs 线性无关，而α1，α2 ，...，αs β线性相关，则向量β必能由α1，α2 ，...，αs 线性表示且表示法唯一。
秩（向量组）
向量组的秩
定义：在向量组α1，α2 ，...，αs 中，如存在r个向量αi1，αi2 ，...，αir 线性相关，再添加任一个αj（j1，2，...，s），向量组αi1，αi2 ，...，αir αj就线性相关，则称αi1，αi2 ，...，αir 是向量组α1，α2 ，...，αs 的一个极大线性无关组。（子集合，无关，再添加就相关）
定理：如αi1，αi2 ，...，αir 与αj1 αj2 ...，αjt 都是向量组α1，α2 ，...，αs 的极大无关组，则r=t。
定义：向量组α1，α2 ，...，αs 的极大线性无关组中所含向量的个数γ称为向量组的秩，记为γ（α1，α2 ，...，αs ）=γ。
只有零向量的向量组，规定其秩为0.
极大线性无关组的等价定义
设向量组αi1，αi2 ，...，αir 是向量组α1，α2 ，...，αs 的 一个部分组，且满足：
（1）αi1，αi2 ，...，αir 线性无关。
（2）任一个向量αj（j1，2，...，s）都能由αi1，αi2 ，...，αir 线性表示。
定理：如α1，α2 ，...，αs 可由β1 β2 ...βt 线性表示，则γ（α1，α2 ，...，αs ）<=γ（β1 β2 ...βt )。
正交化
①
②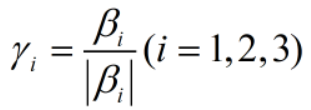
强化阶段
1、证α1α2...αs无关
（1）定义法
(2)
重要结论：
2、线性表示
做证明题方法：
（1)构造方程组，证明方程组有解
（2）找出两个条件：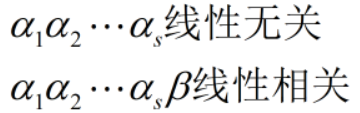
（3）证k≠0（能表出）
（4）反证法（不能表出）
四、方程组
一、Ax=0 基础解系 n-r（A）
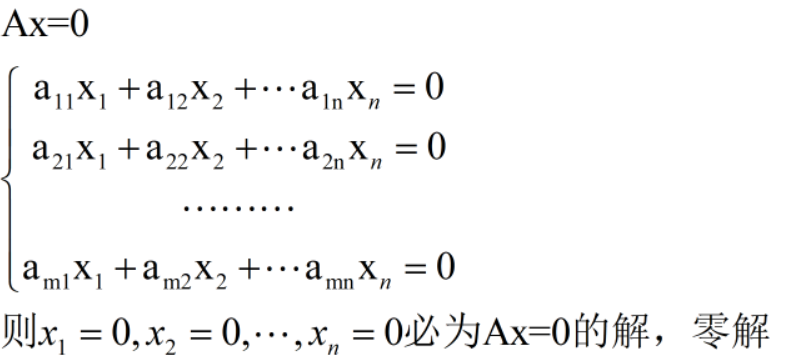
定理：Am✖n X=0有非0解<=>r(A)<n
<=>A的列向量组线性相关。
推论：
1、当m<n时，AX=0必有非0解
2、当m=n时，Ax=0有非零解<=>|A|=0
定理：若Ax=0系数矩阵的秩r(A)=r<n则Ax=0有n-r个线性无关的解，且Ax=0的任一个解都可由这n-r个线性无关的解线性表出。
Ax=0的 基础解系
定理：
二、Ax=b 有解判定 解的结构
解的性质
（1）
（2）
定理：
定理（解的结构）
三、方程组的应用
解方程组手段：
同解变形：1、将两个方程的位置互换
2、将某个方程乘以一个非0的常数
3、将一个方程的k倍加到另一个方程上
五、特征值
一，特征值，特征值向量
定义：设A是n阶矩阵，α是n维非0列向量且Aα=λα，则称λ是矩阵A的特征值，α是矩阵A对应于特征值λ的特征向量。
由Aα=λα，α≠0
=>(λE-A)α=0 (λE-A)x=0
=>α是齐次方程组(λE-A)x=0 的非0解。
（1）由|λE-A|=0，求特征值λi 共n个（含重根）
(2)对（λiE-A）x=0求基础解系，即特征值λi的线性无关的特征向量，写通解得λi所有的特征向量
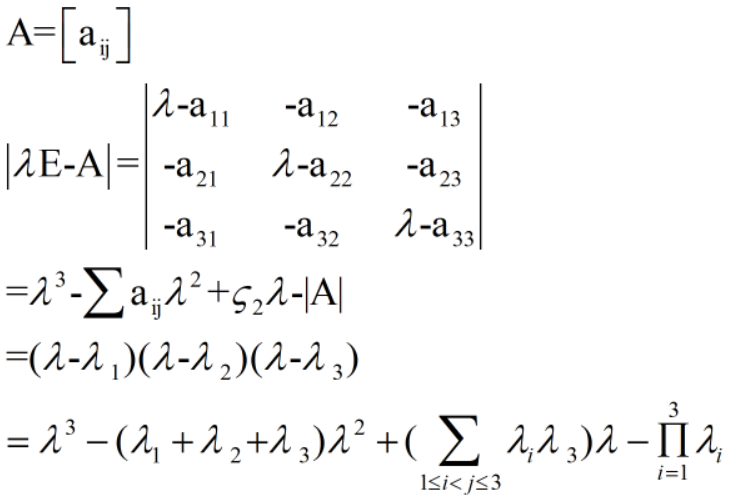
定理：A-n阶
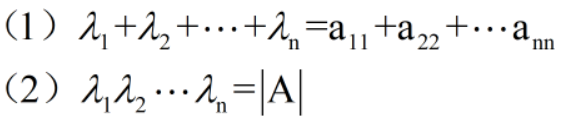
重要结论：
1、如α1，α2都是矩阵A对应于特征值λ的特征向量，则α1+α2≠0时，α1+α2仍是矩阵A对应于特征值λ的特征向量。
2、若α1，α2 分别是矩阵A不同特征值λ1和λ2的特征向量，则α1+α2 不是矩阵A的特征向量。
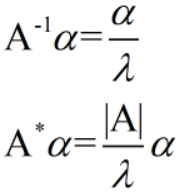
二、相似矩阵
设A，B都是n阶矩阵，如存在可逆矩阵P是P-1AP=B，就称矩阵A相似于矩阵B，B是A的相似矩阵记成A~B。
相似的基本性质：
1、A~A
2、如A~B，则B~A。
3、如A~B，B~C，则A~C。
相似对角化 P-1AP=Λ
如A~Λ，则称矩阵A可相似对角化。
定理：A~Λ<=>A有n个线性无关的特征向量
推论：如A有n个不同的特征值，则A~Λ。
定理：A~Λ<=>λ是A的k重特征值，则λ有k个线性无关的特征向量。
三、实对称矩阵
概念：主对角线不看，其他部分关于主对角线对称分布。
定理：实对称矩阵必可相似对角化。
定理：实对称矩阵不同特征值对应的特征向量相互正交。
定理：实对称矩阵必存在正交矩阵Q使Q-1AQ=QTAQ=Λ
解题基本步骤：
1、求出A的特征值λ1，λ2，λ3
2、求出对应的特征向量α1，α2，α3
3、改特征向量为γ1，γ2，γ3
（1）如特征值不同，只需单位化。
（2）若特征值有重根。
①如特征向量已正交，只需要单位化。
②如特征向量不正交，需Schmidt正交化。
4、构造正交矩阵Q=(γ1，γ2，γ3 )
强化阶
求可逆矩阵P使P-1AP=Λ
1、预处理
2、求特征值λ1λ2λ3
3、求特征向量α1α2α3
4、构造可逆P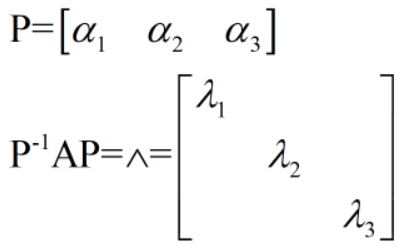
六、二次型
一、基本概念
1、二次型及其矩阵表示
2、标准形
只有平方项，没有其他不同项。
3、规范性
是标准型，并且系数为1，-1，0中的一个。
4、正惯性指数，负惯性指数
标准形系数正负的个数，正惯性指数用p，负惯性指数用q
5、二次型的秩
r(f)=r(A)
6、坐标变换
系数行列式可逆。
7、合同
如CTAC=B,C-可逆矩阵，称矩阵A和B合同，记作
定理1、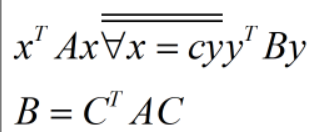
定理2、对任一二次型xTAx，都存在坐标变换可将其化为标准形，即
定理3（惯性定理）二次型经坐标变换其正负惯性指数都不变。
二、标准形（1、配方法2、正交变换法）
1、配方法：先配x1，再配x2,最后配x3,按顺序进行。
2、正交变换法：就是转换为求特征值，和特征向量问题。
三、正定二次型
定义：设二次型f(x)=XTAX,如
，恒有f(x)>0，则称f为正定二次型，二次型矩阵A称为正定矩阵。
定理：经坐标变换不改变二次型的正定性。
定理（正定的充分必要条件）
XTAX正定
<=>p=n
<=>
(即存在可逆C，使CTAC=E)
亦A=DTD,D-可逆
<=>A的特征值全大于0
<=>A的顺序主子式全大于0