FFT
参考blog:
十分简明易懂的FFT(快速傅里叶变换)
快速傅里叶变换(FFT)详解
(下面的图片是来自于这2篇博客里面的,仔细看可以发现右下角有水印……)
系数表示法
一个一元(n)次多项式(f(x))可以被表示为:$$f(x) = sum_{i = 0}^{n}a_{i}x^{i}$$
即用(i)次项的系数来表示(f(x)),展开就是(f(x) = {a_{0}, a_{1}...a_{n}})
点值表示法
把多项式看做一个函数,然后带入(n)个不同的(x),可以得到(n)个不同的(y),每对((x, y))就组成一个点。
其中,(n)个点可以唯一确定一个(n)次多项式。
即用(n)个点来表示一个多项式
一些性质:
系数表达式相乘复杂度(n^2),点值表达式相乘复杂度(O(n)),听上去很神奇的样子。。。
设2个点值表达式分别为:
(f(x) = {(x_{0}, f(x_{0})), (x_{1}, f(x_{1}))... (x_{n}, f(x_{n}))})
(g(x) = {(x_{0}, g(x_{0})), (x_{1}, g(x_{1}))... (x_{n}, h(x_{n})) })
那么相乘得到:
(h(x) = {(x_{0}, f(x_{0}) * g(x_{0})), (x_{1}, f(x_{1}) * g(x_{1})) ... (x_{n}, f(x_{n}) g(x_{n})) })
朴素系数转点值:DFT 复杂度(O(n^2))
朴素点值转系数:IDFT 复杂度(O(n^2))
复数
(z = a + bi),(a)为实部,(b)为虚部。
可以表示坐标系中的一个点((a, b)),同时一一对应向量(vec{ab}),因此也符合向量的相加法则。
在极坐标上可以表示为((r, heta))。
一个性质:((a_1, heta_1) cdot (a_2, heta_2) = (a_1a_2, heta_1 + heta_2))
即模长相乘,幅角相加。
DFT(离散傅里叶变换)
- 从这里开始的所有(n)默认可以表示为(2^k)
原理:对于任意系数多项式转点值表示法,如果随意取(n)个(x)值代入计算,那么每次计算都是(O(n))的,总复杂度(O(n^2)).
如果取一些特殊的(x)值,使得(f(x))可以快速计算,那么就可以在保证正确性的同时优化复杂度。
如果代入一些(x),使得每个(x)的若干次方等于(1),那么说不定我们就可以找到一些特殊性质。那么有哪些(x)符合这个条件呢?
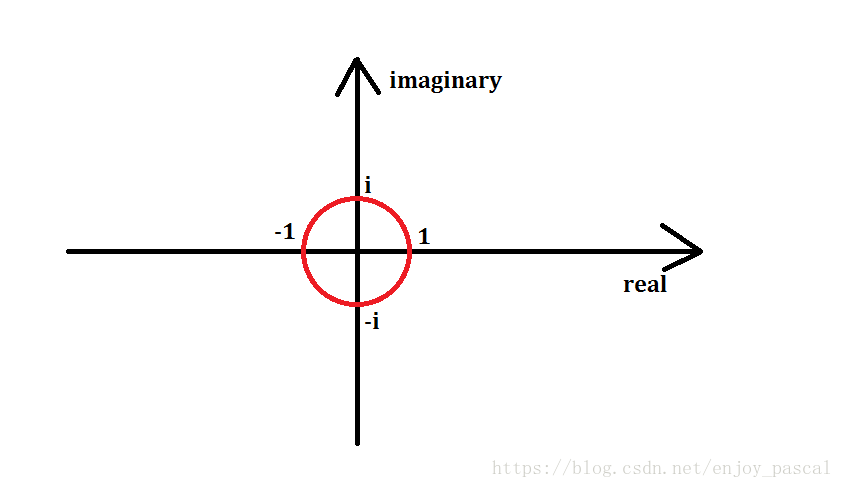
显然(pm 1)和(pm i)都可以做到,但4个数明显不够用。
这个圆圈上面的点都可以做到.
以原点为圆心,画一个半径为1的单位圆,那么单位圆上的所有点都可以经过若干次方得到1.
对这个圆进行(n)等分。
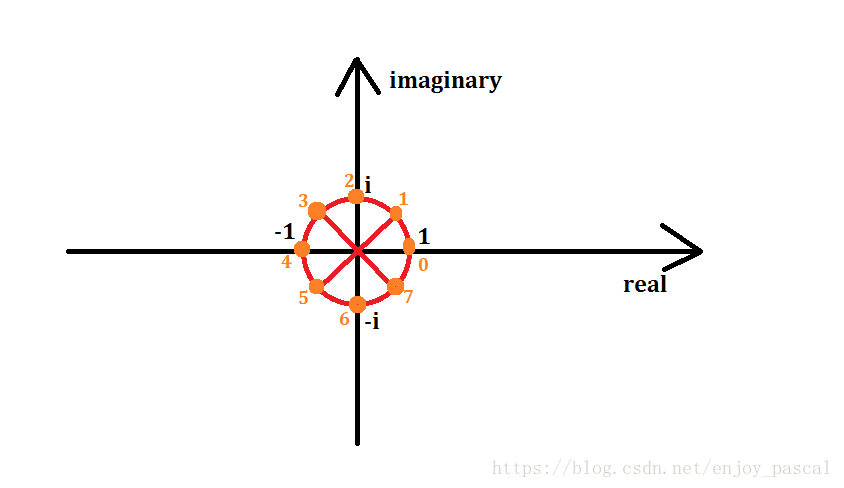
以(n = 8)为例,从((1, 0))开始,逆时针从(0)号开始标号,标到(7)号为止。记编号为(k)的点代表的复数为(w_n^k),那么由模长相乘,幅角相加可知((w_n^1)^k = w_n^k).
其中称(w_n^1)为(n)次单位根,并且每个(w)都可以被求出:
但如果我们暴力代入图中的(w_n^0,w_n^1...w_n^{n - 1}),复杂度还是(n^2),因此我们考虑寻找一下单位根的性质
单位根的性质
(w_n^k = w_{2n}^{2k})
证明:$$w_n^k = cosfrac{k}{n}2pi + i cdot sinfrac{k}{n}2pi$$
显然相等
(w_n^{k + frac{n}{2}} = - w_n^k)
它们所代表的点关于原点对称,所代表的复数实部相反,所代表的向量等大反向
证明:$$w_n^{frac{n}{2}} = cosfrac{frac{n}{2}}{n}2pi + i cdot sinfrac{frac{n}{2}}{n}2pi$$
补充2个等式:
[w_n^0 = w_n^n ]
它们都等于(1),或者(1 + 0i)
FFT(快速傅里叶变换)
目的:系数转点值。
设$$A(x) = sum_{i = 0}^{n - 1}a_ix^i = a_0 + a_1x + a_2x^2+...+a_{n - 1}x^{n - 1}$$
按下标奇偶性把(A(x))分成2半,右边再提一个x.
设$$A_1(x) = a_0 + a_2x + a_4x^2 + ... + a_{n - 2}x^{frac{n}{2} - 1}$$
设(k < frac{n}{2}),代入(w_n^k = x longrightarrow A(x))
再代入(k + frac{n}{2})
再考虑另一半:
代入(k + frac{n}{2})
可以发现:
因此可以得到:
于是可以发现,这2个式子是长得很像的,因此我们可以在求出(A(w_n^k))后(O(1))的求出(A(w_n^{k + frac{n}{2}})).
因为将式子一分为二后,每一部分仍然是一个子问题,因此可以用分治来做到(nlogn)求这个东西。
每次回溯时只扫前面一半序列,即可得到后面一半序列的答案,长度为1时只有一个常数项,可以直接返回。
大致就是把(f(x))和(g(x))分别转换为点值表达,然后(O(n))的处理乘积,得到(h(x))的点值表达
IFFT(快速傅里叶逆变换)
目的:点值转系数
设((y_0, y_1, y_2..., y_{n - 1}))为((a_0, a_1, a_2, ..., a_{n - 1}))的傅里叶变换(点值表达)。
设有另一个向量((c_0, c_1, c_2, ..., c_{n - 1})),满足(c_k = sum_{i = 0}^{n - 1}y_i(w_n^{-k})^i).
即多项式(B(x) = y_0 + y_1x + y_2x^2 + ... + y_{n - 1}x^{n - 1})在(w_n^0, w_n^{-1},w_n^{-2}...w_{n - 1}^{-(n - 1)})处的点值表示。
于是对(c_k = sum_{i = 0}^{n - 1}y_i(w_n^{-k})^i)进行化简
设(S(n) = sum_{i = 0}^{n - 1}x^i),将(w_n^k)代入得:$$S(w_n^k) = 1 + (w_n^k) + (w_n^k)^2 + ... + (w_n^k)^{n - 1}$$
当(k != 0)得,等式两边同乘(w_n^k)得:$$w_n^kS(w_n^k) = w_n^k + (w_n^k)^2 + ... + (w_n^k)^n$$
两式相减得:
(longrightarrow)分子为0,分母不为0
- 当(k != 0)时,(S(w_n^k) = 0);(quad)当(k = 0)时,(S(w_n^0) = n)
继续考虑刚才的式子:(c_k = sum_{j = 0}^{n - 1}a_j (sum_{i = 0}^{n - 1}(w_n^{j - k})^i)) - 当(j != k)时,值为(0);(quad)当(j = k)时,值为(n)
因此:$$c_k = na_k Longrightarrow a_k = frac{c_k}{n}$$
于是我们得到了一个(O(1))把一个点值变成一个系数的方法。
递归实现
不断将当前序列一分为二,递归求解。
但效率过低……
迭代实现
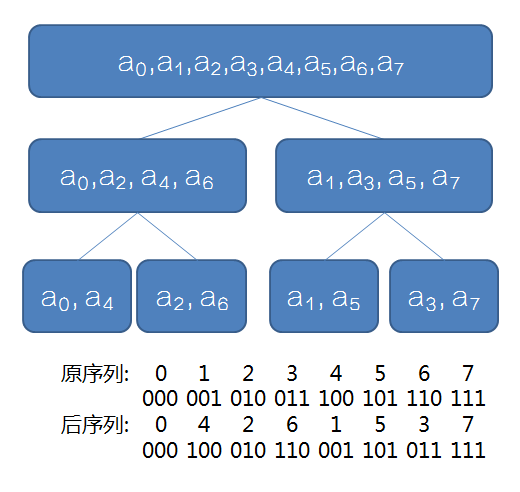
观察到原序列和要求的序列之间有神奇的联系,,,
要求的序列的第i项就是原序列下标二进制的翻转。
因此我们可以(O(n))预处理出要求的序列是怎么排的,然后再不断向上合并。
一些具体一点的东西:
因为求(A_1,A_2)的过程可以看做求一个新的(A),所以是一个子问题,对于分治区间([l, r]),目标是求当前区间的(A)数组,要用到的是当前(A)的(A_1)和(A_2)。
即([l, mid])的(A_1)和([mid + 1, r])的(A_2)。
每次,我们从([l, mid])中的某个位置(A[l + k])中取出当前所求(A)的对应(A_1),从(A[l + k + mid])中取出当前所求(A)的对应的(A_2),然后用这2个值计算出([l ,r])的(A[l + k])和(A[l + k + mid])
#include<bits/stdc++.h>
using namespace std;
#define R register int
#define AC 10001000
#define ld double
#define LL long long
const double pi = acos(-1);
int n, m, maxn, lim = 1, len;
int Next[AC];//预处理出i对应的位置Next[i], 易知i = Next[Next[i]],所以不能交换2次,只能交换1次,不然就换回来了
struct node{
ld x, y;
node (ld xx = 0, ld yy = 0) {x = xx, y = yy;}
}a[AC], b[AC];
node operator * (node x, node y) {return node(x.x * y.x - x.y * y.y, x.x * y.y + x.y * y.x);}
node operator - (node x, node y) {return node(x.x - y.x, x.y - y.y);}
node operator + (node x, node y) {return node(x.x + y.x, x.y + y.y);}
inline int read()
{
int x = 0;char c = getchar();
while(c > '9' || c < '0') c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
void pre()
{
n = read(), m = read();
for(R i = 0; i <= n; i ++) a[i].x = read();
for(R i = 0; i <= m; i ++) b[i].x = read();
while(lim <= n + m) lim <<= 1, ++ len;//寻找长度最接近的,可以覆盖a * b的2^len
for(R i = 0; i < lim; i ++)//一个长度为len的二进制串 = lim - 1
Next[i] = ((Next[i >> 1]) >> 1) | ((i & 1) << (len - 1));
}
//分治的最下面一层是求长度为1的,只有一个常数项的多项式,系数即为给定的系数值
void FFT(node *A, int opt)
{
for(R i = 0; i < lim; i ++)
if(i < Next[i]) swap(A[i], A[Next[i]]);
for(R i = 1; i < lim; i <<= 1)//上一层(被更新层)长度为2i,因为长度为1的不用处理……,所以要< lim,这样才可以保证2i <= lim
{//弧度 = 2pi / 2i = pi / i,那么因为是单位圆上的点,所以横坐标就是cos(弧度), 纵坐标就是sin(弧度)
node W(cos(pi / i), opt * sin(pi / i));//但是在还原为系数的时候用的是w_n^{-k},所以相当于把算出的纵坐标变成相反数,即乘opt
for(R r = i << 1, j = 0; j < lim; j += r)//枚举上一层每段的段首
{
node w(1, 0);//下面枚举上一层的一半,更新j + k时顺便更新j + k + i
for(R k = 0; k < i; k ++, w = w * W)//每次循环一次将w更新为下一个w_n^k
{
node x = A[j + k], y = w * A[j + k + i];
A[j + k] = x + y, A[j + k + i] = x - y;
}
}
}
}
void work()
{
FFT(a, 1);
FFT(b, 1);
for(R i = 0; i < lim; i ++) a[i] = a[i] * b[i];
FFT(a, -1);
for(R i = 0; i <= n + m; i ++) printf("%d ", (int)(a[i].x / lim + 0.5));
}
int main()
{
freopen("in.in", "r", stdin);
pre();
work();
fclose(stdin);
return 0;
}
NTT
用原根代替单位根。
阶
若((a, p) = 1)且(p > 1),那么对于满足(a^n equiv 1quad(mod quad p))最小的(n),称为(a)是模(p)意义下的阶。
原根
设(p in N^+, a in N),若(delta_p(a) = phi(p)),则称(a)为(p)的一个原根,原根个数不唯一。若(p)有原根,那么它一定有(phi(phi(p)))个原根。
数(m)有原根的充要条件是(m = 2, 4, p^a,2p^a),其中(p)为奇素数(a ge 1)
若(p)为素数,(g)是(p)的原根,那么(g^i\%p(1 < g < p, 0 < i < p))的结果互不相同
一个结论:
(p)为(998244353)时,原根为(3).
求任意质数的原根:对于质数(p),质因子分解(p - 1)得到(p_i),若$$g^{frac{p - 1}{p_i} != 1} quad (mod quad p)$$
恒成立,则(g)为(p)的原根。
实现方式:
基于普通FFT,对于opt = 1的情况,直接用(g^{frac{p - 1}{p_i}})代替,否则需要用(g^{-frac{p - 1}{p_i}})来代替,即(g^{-k} = frac{1}{g^k} = (frac{1}{g})^k = inv[g] ^ k)
(在FFT中,因为(w^{-k})就相当于是向反方向转了相同角度,所以只需要乘(-1)即可)
#include<bits/stdc++.h>
using namespace std;
#define R register int
#define p 998244353
#define AC 10001000
#define LL long long
const int G = 3, Gi = 332748118;
int n, m, lim = 1, len;
int a[AC], b[AC], rev[AC];
inline int read()
{
int x = 0;char c = getchar();
while(c > '9' || c < '0') c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
int qpow(int x, int have)
{
int rnt = 1;
while(have)
{
if(have & 1) rnt = 1LL * rnt * x % p;
x = 1LL * x * x % p, have >>= 1;
}
return rnt;
}
void pre()
{
n = read(), m = read();
for(R i = 0; i <= n; i ++) a[i] = read();
for(R i = 0; i <= m; i ++) b[i] = read();
while(lim <= n + m) lim <<= 1, ++ len;
for(R i = 0; i < lim; i ++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
void NTT(int *A, int opt)
{
for(R i = 0; i < lim; i ++)
if(i < rev[i]) swap(A[i], A[rev[i]]);
for(R i = 1; i < lim; i <<= 1)
{
//int W = qpow((opt > 0) ? G : Gi, (p - 1) / (i << 1));
LL W = qpow(opt == 1 ? G : Gi , (p - 1) / (i << 1));
for(R r = i << 1, j = 0; j < lim; j += r)
for(R w = 1, k = 0; k < i; k ++, w = (1LL * w * W) % p)
{
int x = A[j + k], y = 1LL * w * A[j + k + i] % p;
A[j + k] = (x + y) % p, A[j + k + i] = (x - y + p) % p;
}
}
}
void work()
{
NTT(a, 1);
NTT(b, 1);
for(R i = 0; i < lim; i ++) a[i] = 1LL * a[i] * b[i] % p;
NTT(a, -1);
int inv = qpow(lim, p - 2);//lim的逆元
for(R i = 0; i <= n + m; i ++) printf("%lld ", 1LL * a[i] * inv % p);
printf("
");
}
int main()
{
freopen("in.in", "r", stdin);
pre();
work();
fclose(stdin);
return 0;
}