一、图的定义
图是一种复杂的非线性结构。
在线性结构中,数据元素之间满足唯一的线性关系,每个数据元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继;
在树形结构中,数据元素之间有着明显的层次关系,并且每个数据元素只与上一层中的一个元素(双亲节点)及下一层的多个元素(孩子节点)相关;
而在图形结构中,节点之间的关系是任意的,图中任意两个数据元素之间都有可能相关。
图G由两个集合V(顶点Vertex)和E(边Edge)组成,定义为G=(V,E)
1、无向图和有向图
对于一个图,若每条边都是没有方向的,则称该图为无向图。图示如下:

因此,(Vi,Vj)和(Vj,Vi)表示的是同一条边。注意,无向图是用小括号,而下面介绍的有向图是用尖括号。
无向图的顶点集和边集分别表示为:
V(G)={V1,V2,V3,V4,V5}
E(G)={(V1,V2),(V1,V4),(V2,V3),(V2,V5),(V3,V4),(V3,V5),(V4,V5)}
对于一个图G,若每条边都是有方向的,则称该图为有向图。图示如下。

因此,<Vi,Vj>和<Vj,Vi>是两条不同的有向边。注意,有向边又称为弧。
有向图的顶点集和边集分别表示为:
V(G)={V1,V2,V3}
E(G)={<V1,V2>,<V2,V3>,<V3,V1>,<V1,V3>}
2、无向完全图和有向完全图
我们将具有n(n-1)/2条边的无向图称为无向完全图。同理,将具有n(n-1)条边的有向图称为有向完全图。
3、顶点的度
对于无向图,顶点的度表示以该顶点作为一个端点的边的数目。比如,图(a)无向图中顶点V3的度D(V3)=3
对于有向图,顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目,出度是以该顶点为起点的出边数目,该顶点的度等于其入度和出度之和。比如,顶点V1的入度ID(V1)=1,出度OD(V1)=2,所以D(V1)=ID(V1)+OD(V1)=1+2=3
记住,不管是无向图还是有向图,顶点数n,边数e和顶点的度数有如下关系:
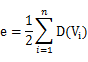
因此,就拿有向图(b)来举例,由公式可以得到图G的边数e=(D(V1)+D(V2)+D(V3))/2=(3+2+3)/2=4
5、路径,路径长度和回路
路径,比如在无向图G中,存在一个顶点序列Vp,Vi1,Vi2,Vi3…,Vim,Vq,使得(Vp,Vi1),(Vi1,Vi2),…,(Vim,Vq)均属于边集E(G),则称顶点Vp到Vq存在一条路径。
路径长度,是指一条路径上经过的边的数量。
回路,指一条路径的起点和终点为同一个顶点。
6、连通图(无向图)
连通图是指图G中任意两个顶点Vi和Vj都连通,则称为连通图。比如图(b)就是连通图。下面是一个非连通图的例子。

上图中,因为V5和V6是单独的,所以是非连通图。
7、强连通图(有向图)
强连通图是对于有向图而言的,与无向图的连通图类似。
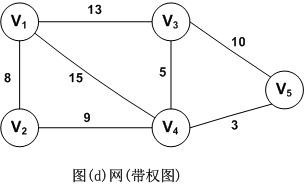
8、网
带”权值”的连通图称为网。如图所示。
二、存储结构、遍历算法
对于无无向图,常用的描述方式是邻接方式:邻接矩阵、邻接链表和邻接数组
1、邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

看一个实例,下图左就是一个无向图。

若图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

这里的wij表示(vi,vj)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值(通常可设为-1),也就是一个不可能的极限值。下面左图就是一个有向网图,右图就是它的邻接矩阵
邻接矩阵有如下特点:
(1)对于无向图,邻接矩阵是对称的;
(2)方便判断任意两顶点是否有边(对应arc[i][j]不为0);
(3)方便找出任一顶点烦人所有邻接点,对于顶点vi,邻接点就是邻接矩阵的第i行中不为0的点;
(4)方便计算顶点的度:
对于无向图,顶点的度为对应行或列中非0元素的个数
对于有向图,出度为对应行中非0元素的个数,入度为对应列中非0元素的个数。
使用邻接矩阵时,要确定邻接至或邻接于一个给定节点的集合需要用时o(n),增加或删除一条边的时间复杂度是o(1)。
邻接矩阵比较适合于稠密图。
无权无向图的邻接矩阵实现:
1 class adjacencygraph 2 { 3 private: 4 int n; //节点数 5 int e; //边数 6 int **a; //邻接数组 7 int noedge; //表示边不存在 8 9 public: 10 adjacencyWDigraph(int numberofVertices=0, int thenodega=0) 11 { 12 if(numberofVertices<0) 13 cout << "number of Vertices must be >=0" << endl; 14 n=numberofVertices; 15 e=0; 16 noedge = thenodega; 17 a= new int[n+1][n+1]; 18 19 for(int i=1;i<=n;i++) 20 for(int j=1;j<=n;j++) 21 a[i][j]=noedge; 22 } 23 24 ~adjacencyWDigraph(){delete [] a;} 25 26 bool existEdge(int i,int j) const 27 { 28 if(i<1 || j<1 || i<n || j<n || a[i][j]=noedge) 29 return false; 30 else 31 return true; 32 } 33 34 void insertEdge(int i, int j) 35 { 36 if(i<1 || j<1 || i<n || j<n ) 37 cout << "(" << i << "," << j <<") is not a permisible edge" <<endl; 38 39 if(a[i][j]==noedge) //新边 40 e++; 41 a[i][j]=1; 42 43 } 44 45 }
2、邻接链表
邻接链表适合于稀疏图。可以使用类型为chain类型的数组aList来描述所以的邻接表,对于n个节点的图,将alist的长度设为n。aList[i-1]表示顶点i的邻接表。

邻接链表的特点:
(1)方便查找顶点的所有邻接点;
(2)节约稀疏图的存储空间,需要N个头指针和2E个节点
(3)对于读的计算:
无向图的度即为链表的长度;
有向图只能计算出度,为链表的长度。对于入度,需要构造“逆邻接表”(指向自己的边)
(4)不能判断两个顶点之间是否存在边
无向图的链表形式实现如下所示:
1 struct chainNode //链表节点 2 { 3 // data member 4 int element; //节点编号 5 chainNode *next; //指针 6 7 }; 8 9 10 class linkedGraph 11 { 12 private: 13 int n; //顶点数 14 int e; //边数 15 chainNode *aList; //邻接表 16 17 public: 18 linkedGraph(int numberofVertices=0) 19 {//构造函数 20 if(numberofVertices<0) 21 cout << "number of Vertices must be >=0"<<endl; 22 n=numberofVertices; 23 e=0; 24 aList=new chainNode[n+1]; 25 } 26 27 ~linkedGraph() {delete [] aList;} 28 29 bool indexofchain(chainNode* tmp, const int j) 30 {//当且仅当tmp中存在j时返回true 31 while(tmp !=NULL && tmp->element !=j) 32 { 33 // move to next node 34 tmp = tmp->next; 35 } 36 if (tmp == NULL) 37 return false; 38 else 39 return true; 40 } 41 42 bool existEdge(int i, int j) const 43 {//返回true,当且仅当(i,j)是一条边 44 if(i<1 || j<1 || i<n || j<n || !Indexofchain(aList[i],j)) 45 return false; 46 else 47 return true; 48 } 49 50 void insertEdge(int v1,int v2) const 51 {//插入一条边(i,j) 52 if (v1 < 1 || v2 < 1 || v1 > n || v2 > n || v1 == v2) 53 cout << "(" << v1 << "," << v2 << ") is not a permissible edge"; 54 55 if (!Indexofchain(aList[i],j)) 56 {// 新边,将其插入链表的首部,因为在首部插入元素的时间为0(1) 57 chainNode *tmp=NULL; 58 tmp->element=v2; 59 tmp->next=aList[v1] 60 aList[v1]=tmp; 61 delete tmp; 62 63 e++; 64 } 65 } 66 67 void eraseEdge(int v1, int v2) const 68 { 69 chainNode *tmp= aList[v1], *lastNode=NULL; 70 71 if(v1 >= 1 && v2 >= 1 && v1 <= n && v2 <= n && Indexofchain(aList[i],j)) 72 { 73 74 while(tmp->element !=j) 75 { 76 lastNode=tmp; 77 tmp = tmp->next; 78 } 79 lastNode->next=tmp->next; 80 81 e--; 82 delete tmp; 83 delete lastNode; 84 } 85 } 86 87 int outdegree( int theVertex) const 88 { 89 if(theVertex >= 1 && theVertex <= n ) 90 { 91 chainNode *tmp= aList[theVertex]; 92 int d=0; 93 while(tmp!=NULL) 94 d++; 95 96 delete tmp; 97 return d; 98 } 99 return 0; 100 } 101 102 int indegree (int theVertex) const 103 { 104 if(theVertex >= 1 && theVertex <= n ) 105 { 106 int d=0; 107 for(int i=0;i<n;i++) 108 if(Indexofchain(aList[i],theVertex)) 109 d++; 110 return d; 111 } 112 return 0; 113 } 114 115 }
三、图的遍历
1、 深度优先遍历
深度优先遍历,也有称为深度优先搜索,简称DFS。其实,就像是一棵树的前序遍历。其基本思路是:
a) 假设初始状态是图中所有顶点都未曾访问过,则可从图G中任意一顶点v为初始出发点,首先访问出发点v,并将其标记为已访问过。
b) 然后依次从v出发搜索v的每个邻接点w,若w未曾访问过,则以w作为新的出发点出发,继续进行深度优先遍历,直到图中所有和v有路径相通的顶点都被访问到。
c) 若此时图中仍有顶点未被访问,则另选一个未曾访问的顶点作为起点,重复上述步骤,直到图中所有顶点都被访问到为止。
图示如下:

注:红色数字代表遍历的先后顺序,所以图(e)无向图的深度优先遍历的顶点访问序列为:V0,V1,V2,V5,V4,V6,V3,V7,V8
对于深度优先遍历,对于n个顶点e条边的图来说,邻接矩阵由于是二维数组,要查找某个顶点的邻接点需要访问矩阵中的所有元素,因为需要O(n2)的时间。而邻接表做存储结构时,找邻接点所需的时间取决于顶点和边的数量,所以是O(n+e)。显然对于点多边少的稀疏图来说,邻接表结构使得算法在时间效率上大大提高。
其伪代码实现如下
1 void DFS (Vertex V) 2 { 3 Visited[V]=true; 4 for (V的每个邻接点W) 5 if(!Visited[W]) 6 DFS(W); 7 }
2、 广度优先搜索遍历
广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是:
a) 首先访问出发点Vi
b) 接着依次访问Vi的所有未被访问过的邻接点Vi1,Vi2,Vi3,…,Vit并均标记为已访问过。
c) 然后再按照Vi1,Vi2,… ,Vit的次序,访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过,依此类推,直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。
图示如下:

其伪代码实现如下
1 void BFS (Vertex V) 2 { 3 visited[V] = true; 4 Enqueue(V,Q); 5 while(!IsEmpty(Q)) 6 { 7 V=Dequeue(Q); 8 for(V的每个邻接点W) 9 if(!visited[W]) 10 { 11 visited[W] = true; 12 Enqueue(W,Q); 13 } 14 } 15 }
对比图的深度优先遍历与广度优先遍历算法,会发现,它们在时间复杂度上是一样的,不同之处仅仅在于对顶点的访问顺序不同。可见两者在全图遍历上是没有优劣之分的,只是不同的情况选择不同的算法。
数据结构之图(存储结构、遍历)-梦醒潇湘love http://blog.chinaunix.net/uid-26548237-id-3483650.html
数据结构和算法系列17 图 - 永远的麦子 http://www.cnblogs.com/mcgrady/archive/2013/09/23/3335847.html