卷积神经网络(CNN)可以很好的处理二维平面图像的问题。然而,对球面图像进行处理需求日益增加。例如,对无人机、机器人、自动驾驶汽车、分子回归问题、全球天气和气候模型的全方位视觉处理问题。
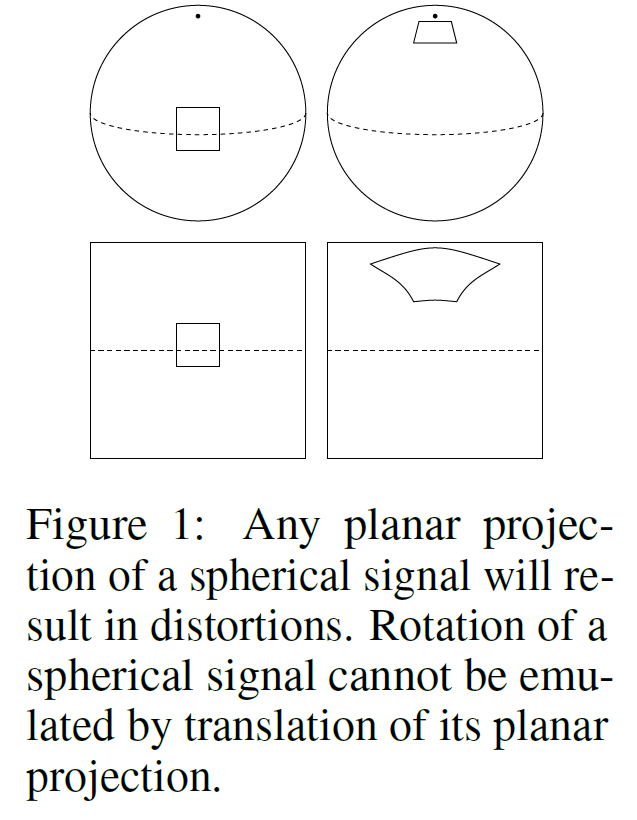
将球形信号的平面投影作为卷积神经网络的输入的这种Too Naive做法是注定要失败的,Cnns的巨大成就来源于局部感受野的权值共享,而多层结构总能找到不同rect的相同目标,给出响应。而对于球形图像,一个目标在图片的不同位置是发生形变的,若要使用CNNs直接共享,构建的局部感受野理应描述这种转换。如下图所示,而这种平面投影引起的空间扭曲会导致CNN无法共享权重。
We propose a definition for the spherical cross-correlation that is both expressive and rotation-equivariant. The spherical correlation satisfies a generalized Fourier theorem, which allows us to compute it efficiently using a generalized(non-commutative) Fast Fourier Transform (FFT) algorithm. We demonstrate the computational efficiency, numerical accuracy, and effectiveness of spherical CNNs applied to 3D model recognition and atomization energy regression.
如何使三维图像由二维图像重构出来,解决在不同位置产生形变问题,经典的FFT方法和李群模型就成为这种桥梁。
关于SO3 作为刚体变换的阐述,参考:半闲居士视觉SLAM十四讲笔记(3)三维空间刚体运动 - par..._CSDN博客 。
wocao,这个大纲写的更简洁明了:高翔《视觉SLAM十四讲》从理论到实践。
区分出三维图像和平面的细微差别,把球面图像看做是三维流形,把球面展开为离散的三维李群,把SO(3)的关系用CNNs的高层进行表示。
As shown in Figure 1, there is no good way to use translational convolution or cross-correlation1 to analyze spherical signals. The most obvious approach, then, is to change the definition of crosscorrelation by replacing filter translations by rotations. Doing so, we run into a subtle but important difference between the plane and the sphere: whereas the space of moves for the plane (2D translations) is itself isomorphic to the plane, the space of moves for the sphere (3D rotations) is a different, three-dimensional manifold called SO(3)2. It follows that the result of a spherical correlation (the output feature map) is to be considered a signal on SO(3), not a signal on the sphere, S2. For this reason, we deploy SO(3) group correlation in the higher layers of a spherical CNN (Cohen and Welling, 2016).
The implementation of a spherical CNN (S2-CNN) involves two major challenges. Whereas a square grid of pixels has discrete translation symmetries, no perfectly symmetrical grids for the sphere exist. This means that there is no simple way to define the rotation of a spherical filter by one pixel. Instead, in order to rotate a filter we would need to perform some kind of interpolation. The other challenge is computational efficiency; SO(3) is a three-dimensional manifold, so a naive implementation of SO(3) correlation is O(n6).
球形CNNs的两个难点:图像网格化的粒度,多大的粒度分解能保证重建的准确性;SO(3)的三维流形计算复杂度问题,时间复杂度是O(n6)的。
........................................
The Key moments:
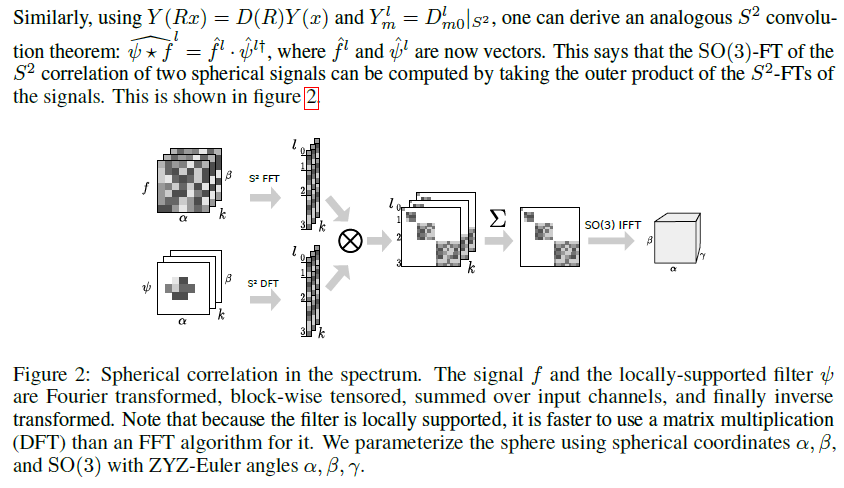
使用G-FFT进行快速相关性卷积,的相关结构。It is well known that correlations and convolutions can be computed efficiently using the Fast Fourier Transform (FFT). This is a result of the Fourier theorem, which states that[f = ^ f ^ . Since the FFT can be computed in O(n log n) time and the product has linear complexity, implementing the correlation using FFTs is asymptotically faster than the naive O(n2) spatial implementation.
.................
.......................................
最重要的一点,Our code is available at: https://github.com/jonas-koehler/s2cnn .
实验效果:
Results We evaluate by RMSE and compare our results to Montavon et al. (2012) and Raj et al. (2016) (see table 3). Our learned representation outperforms all kernel-based approaches and a MLP trained on sorted Coulomb matrices. Superior performance could only be achieved for an MLP trained on randomly permuted Coulomb matrices. However, sufficient sampling of random permutations grows exponentially with N, so this method is unlikely to scale to large molecules.
文中定义了S2和SO(3)的互相关,并分析了它们的属性,进而实现了一个通用的RRT相关算法。实验的数值结果证实了该算法的稳定性和准确性,即使在深度网络上依然有效。
总之,在准确率、可扩展性、等方面是综合最有前途的一个三维网络。
进一步优化:
For intrinsically volumetric tasks like 3D model recognition, we believe that further improvements can be attained by generalizing further beyond SO(3) to the roto-translation group SE(3). The development of Spherical CNNs is an important first step in this direction. Another interesting generalization is the development of a Steerable CNN for the sphere (Cohen and Welling, 2017), which would make it possible to analyze vector fields such as global wind directions, as well as other sections of vector bundles over the sphere.
把SO(3)上的计算往SE(3)上进行转化,把旋转相关性变换到切空间的平移SE(3),应该可以达到新的加速效果。
Appendix:
李群与李代数
三维旋转矩阵构成了特殊正交群SO(3),而变换矩阵构成了特殊欧氏群SE(3)
![]()
![]()
但无论SO(3),还是SE(3),它们都不符合加法封闭性,即加之后不再符合旋转矩阵的定义,但是乘法却满足,将这样的矩阵称为群。即只有一种运算的集合叫做群。
群记作G=(A, .),其中A为集合,.表示运算。群要求运算满足以下几个条件:
(1)封闭性。(2)结合律。
(3)幺元。一种集合里特殊的数集。
(4)逆。
可以证明,旋转矩阵集合和矩阵乘法构成群,而变换矩阵和矩阵乘法也构成群。
介绍了群的概念之后,那么,什么叫李群呢?
李群就是连续(光滑)的群。一个刚体的运动是连续的,所以它是李群。
每个李群都有对应的李代数。那么什么叫李代数呢?
李代数就是李群对应的代数关系式。
李群和李代数之间的代数关系如下:
![]()
可见两者之间是指数与对数关系。
那么exp(φ^)是如何计算的呢?它是一个矩阵的指数,在李群和李代数中,它称为指数映射。任意矩阵的指数映射可以写成一个泰勒展开式,但是只有在收敛的情况下才会有结果,它的结果仍然是一个矩阵。

同样对任意一元素φ,我们亦可按此方式定义它的指数映射:

由于φ是三维向量,我们可以定义它的模长θ和方向向量a满足使φ=θa。那么,对于a^,可以推导出以下两个公式:
设a=(cosα, cosβ, cosγ),可知(cosα)^2+(cosβ)^2+(cosγ)^2=1
(1)a^a^=aaT-I
(2)a^a^a^=-a^
上面两个公式说明了a^的二次方和a^的三次方的对应变换,从而可得:
exp(φ^)=exp(θa^)=∑(1/n!(θa^)n)=...=a^a^+I+sinθa^-cosθa^a^=(1-cosθ)a^a^+I+sinθa^=cosθI+(1-cosθ)aaT+sinθa^.
回忆前一讲内容,它和罗德里格斯公式如出一辙。这表明,so(3)实际上就是由旋转向量组成的空间,而指数映射即罗德里格斯公式。通过它们我们把so(3)中任意一个向量对应到了一个位于SO(3)中的旋转矩阵。反之,如果定义对数映射,我们也能把SO(3)中的元素对应到so(3)中:

但通常我们会通过迹的性质分别求解转角和转轴,那种方式会更加省事一些。
OK,讲了李群和李代数的对应转换关系之后,有什么用呢?
主要是通过李代数来对李群进行优化。比如说,对李群中的两个数进行运算,对应的他们的李代数会有什么变化?
首先是,两个李群中的数进行乘积时,对应的李代数是怎么样的变化,是不是指数变化呢?但是注意,李群里的数是矩阵,不是常数,所以不满足ln(exp(A+B))=A+B,因为A,B是矩阵,不是常数,那么是怎么的对应关系呢?