数论学习小记 其之三 Gcd与Lcm

关于Gcd的欧几里得算法，以及Gcd与Lcm的关系在《数论学习小记 其之一》中有记录，这里就不重复了。

经常做一些与Gcd和Lcm有关的题目，思路有许多相近之处，放在一起总结，遇到新题会继续更新。

一个结论

摘自：如何证明gcd(a,b) = gcd(a+b, lcm(a,b))_百度知道

QQ截图20140122100415

Uva 11388 GCD LCM

题意：给定两个整数G和L，找出两个整数a和b，使得二者的最大公约数为G，最小公倍数为L，如果有多组解，输出a<=b且a最小的解，若无解输出-1

思路：根据Gcd和Lcm的性质可知：L=(a*b)/G,则a*b=L*G,由于G是a和b的约数，因此a和b可以写成G*x,G*y,则等式变为：L/G=x*y。若L%G!=0，则无解，否则取x为1即可。也就是说，如果有解，最小就是G，然后另一个数就是L。

#include <cstdio>

int Gcd (int a,int b)
{
    return !b?a:Gcd(b,a%b);
}

int main ()
{
    int T;
    scanf("%d",&T);
    while (T--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if (b%a==0)
            printf("%d %d
",a,b);
        else
            printf("-1
");
    }
    return 0;
}

Zoj 1577 GCD & LCM

很经典的一道题，本题参考了

ZOJ 1577 GCD & LCM - bingshen的专栏 - 博客频道 - CSDN.NET

zoj 1577 gcd(x,y) * lcm(x,y) = x*y - NeverLoseHeart. - 博客频道 - CSDN.NET

题意：给出两个数x,y，求有多少组p,q，满足gcd(p,q) = x且 lcm(p,q) = y。

无标题

两个很易得的结论：

lcm（x，y）/ gcd(x,y)  = (x / gcd(x,y)) * (y / gcd(x,y))

lcm（x，y）* gcd(x,y)  = x*y

假设g=gcd(p,q)，l=lcm(p,q)，key=l/g，如果l%g!=0则无解。

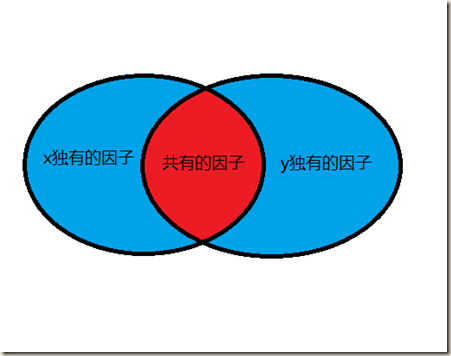
l是p和q公共的素因子的并集，而g则是交集(图中红色部分)，于是key的意思就是l刚好比g多的一部分素因子(图中蓝色部分)

于是我们可以选择这些素因子和g组合得到了p，另一部分和g组合得到了q

假设key的素因子个数（重复的不算）有n个，那么选择方案就有：C(n,0)+C(n,1)+C(n,2)+...+C(n,n)，这个式子的和为2^n。

重复的因子不算个数，因为同1个素因子必须全部在p中或者全部在q中，如果同时属于p和q，GCD将增大。

本题不用筛素也可以。

#include <cstdio>

const int N=1200;

int prime[N],np=0;
bool tag[N];

void Prime ()
{
    for (int i=2;i<N;i++) if (tag[i]==false)
    {
        prime[np++]=i;
        for (int j=i+i;j<N;j+=i)
            tag[j]=true;
    }
}

int split (int n)   //计算素因子(不重复)的个数
{
    int ans=0;
    for (int i=0;prime[i]*prime[i]<=n;i++)
    {
        if (n%prime[i]==0)
        {
            ans++;
            while (n%prime[i]==0)
                n/=prime[i];
        }
    }
    if (n>1)
        ans++;
    return ans;
}

int main ()
{
    int a,b;
    Prime ();
    while (~scanf("%d%d",&a,&b))
    {
        if (b%a!=0)
        {
            printf("0
");    //有可能会是0种组合
            continue;
        }
        int t=split(b/a);
        int ans=1;
        for (int i=1;i<=t;i++)
            ans*=2;
        printf("%d
",ans);
    }
    return 0;
}

Hoj 2010 GCD & LCM Inverse

题目链接：http://acm.hit.edu.cn/hoj/problem/view?id=2010

题意：已知两个数的gcd和lcm求这两个数a, b，多解时要求a+b最小

思路：a/gcd * b/gcd = lcm/gcd，还有一个常识性质的性质：a*b为定值时，a和b相差越小，a+b越小。所以从lcm/gcd的平方根开始枚举a即可。

#include <cstdio>
#include <cmath>

long long Gcd (long long a,long long b)
{
    return !b?a:Gcd(b,a%b);
}

int main ()
{
    long long a,b;
    while (~scanf("%lld%lld",&a,&b))
    {
        long long tmp=b/a,i;
        for (i=sqrt(1.0*tmp);i>=1;i--)
            if (tmp%i == 0)
            {
                b=tmp/i;
                if (Gcd(i,b) == 1)
                    break;
            }
        printf("%lld %lld
",a*i,a*b);
    }
    return 0;
}

uva 10791 - Minimum Sum LCM

题意：求几个最小公倍数为n的数的最小和

参考了：http://blog.csdn.net/goomaple/article/details/8550381

两个最小公倍数为n的数的和不一定最小，例如30=（5*6）=(2*3*5)  5+6>2+3+5

应该是n的各个质因子的相应次方数之和，但要注意几个细节：
（1）当n = 1时，应输出2（1*1=1,sum=1+1=2）；
（2）当n是素数的时候，输出n+1（n*1=n,sum=n+1）；
（3）当只有单质因子时，sum=质因子相应次方+1；
（4）当N=2147483647时，它是一个素数，此时输出2147483648，但是它超过int范围，应考虑用long long。

#include <cstdio>

const int N=100005;

long long p[N],pNum[N],Num;
int prime[N],np=0;
bool tag[N];

void Prime ()
{
    for (int i=2;i<N;i++) if (tag[i]==false)
    {
        prime[np++]=i;
        for (int j=i+i;j<N;j+=i)
            tag[j]=true;
    }
}

void split (int n)
{
    Num=0;//np为素数个数,注意int相乘有可能会超int可表示的范围
    for (int i=0;i<np && (long long)prime[i]*prime[i]<=n;i++)
    {
        if (n%prime[i]==0)
        {
            p[Num]=prime[i];
            pNum[Num]=0;
            while(n%prime[i]==0)
            {
               pNum[Num]++;
               n/=prime[i];
            }
            Num++;
        }
    }
    if (n>1) p[Num]=n,pNum[Num++]=1;
}

int POW (int n,int index)
{//乘方次数不会很大，没必要二分计算
    int ans=1;
    for (int i=1;i<=index;i++)
        ans*=n;
    return ans;
}

int main ()
{
    int n,Cas=1;
    Prime ();
    while (scanf("%d",&n),n)
    {
        printf("Case %d: ",Cas++);
        if (n==1)   //////
        {
            printf("2
");
            continue;
        }
        split(n);
        if (Num==1)  //只有一个质因子(素数和素数的倍数)
        {
            printf("%lld
",(long long)POW(p[0],pNum[0])+1); //因为至少要两个数，另一个数是1
            continue;
        }
        int ans=0;
        for (int i=0;i<Num;i++)
            ans+=POW(p[i],pNum[i]);
        printf("%d
",ans);
    }
    return 0;
}
//1822500000=2^5 * 3^6 * 5^7

poj 2429 GCD & LCM Inverse

题意和上面Hoj的那道题完全一样，只是数据规模变大，如果用c++写，那么必须要用Pollard_rho大数因子分解，这部分我还不熟练，待熟练之后回来补上。

如果用java写，那时间比较宽松，是可以过的，c++时限2000ms，下面的java代码 5516ms 过了……。

以下的java代码摘自：poj 2429 数学题 简单解法 - Because Of You - 博客园

import java.util.*;
import java.io.*;
import java.lang.Math;
public class Main{
    static long gcd(long a,long b)
    {
        long tmp;
        while(b!=0)
        {
            a%=b;
            tmp=a;
            a=b;
            b=tmp;
        }
        return a;
    }
    static long lcm(long a,long b)
    {
        return a/gcd(a,b)*b;
    }
    public static void main(String args[]){
        Scanner cin = new Scanner (System.in);
        long a,b,c,i;
        while(cin.hasNext())
        {
            a=cin.nextLong();
            b=cin.nextLong();
            c=b/a;
            for(i=(long)Math.sqrt(c);i>=1;i--)//a*i+b/i随i的增大而减小
            {
                if(c%i==0&&gcd(i,c/i)==1)
                {
                    System.out.println((a*i)+" "+(b/i));//b/i肯定大于a*i
                    break;
                }
            }
        }
    }
}

遗留问题

LightOJ 1289 涉及节省空间的素数筛法，会在下一篇博文中总结，也可以参考我再csdn的题解：

LightOJ 1289 LCM from 1 to n (节省空间的素数筛法+n个数的最小公倍数) - whyorwhnt的专栏 - 博客频道 - CSDN.NET

LightOJ 1215 还没有仔细想，这里有篇题解：lightoj 1215 - 妮king狼 - 博客园

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/whyorwhnt/p/3529487.html