1.首先需要使用 罗尔定理
函数f(x)在闭区间[a,b]连续在开区间(a,b)可微,如果f(a)=f(b),那么至少存在一点c使函数导数f'(c)=0
注意需要再(a,b)可微,如果函数有角点,断点,尖点,那么就不一定存在c,使f'(c)=0成立,(当然也有可能成立,如果有其他可做水平切线的点0
涉及的图片参考http://www.cnblogs.com/wdfrog/p/5956840.html
注意f(a)=f(b)=0 等于0不是必需,因为只要f(a)=f(b)那么就可通过上下平移得到f(a)=0
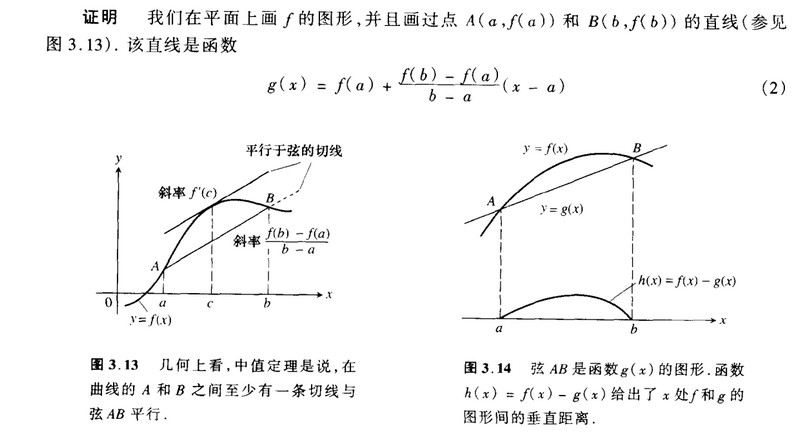
2.根据罗尔定理,可以导出拉格朗日中值定理即
符合上面条件并且 f(a)<>f(b)时
至少能找到一点使 f'(c)=[f(b)-f(a)] / (b-a)



柯西中值定理
条件:设函数 满足
⑴在闭区间 上连续;
⑵在开区间 内可导;
⑶对任意 x属于(a,b),g'(x)<>0 ,
那么在 内至少有一点 ,使得[f(b)-f(a)]/[g(b)-g(a)]=f'(ξ)/g'(ξ)成立
与拉氏定理的联系
在柯西中值定理中,若取g(x)=x时,则其结论形式和拉格朗日中值定理的结论形式相同。
因此,拉格朗日中值定理为柯西中值定理的一个特例;反之,柯西中值定理可看作是拉格朗日中值定理的推广。
证明
洛必达法则与证明



注意在[x0,x]区间上,存在一点c使柯西中值定理成立,又因为f(x0)=g(x0)=0 所以两边同时取lim_(x->x0+)时等式成立
由于 lim_(x->x0) f'(x)/g'(x) 本质上还是lim_(x->x0) f(x)/g(x) (--都是关于x的有真函数之比 ) 所以强形式的洛必达法则可以迭代使用(连续使用)

上面的条件一表示当x->a时f(x),F(x)都趋于0,对应下面的辅助函数f1(a)=F1(a)=0

不支持迭代使用的洛必达法则



注意 lim_(x->a) f'(x)/g'(x) <> f'(x)/g'(x) 所以该形式是不支持迭代使用的,当碰到第一次求导后还是0/0的情况就要使用加强形式的定理