前言
但三角形的四心用文字语言表述时,许多学生还可以对付一阵,若换成向量形式的符号语言,则大多就哑口无言了,所以有必要将三角形四心的向量表示形式好好作以总结储备。
三角形重心
- 重心:三角形的三条中线的交点。
- 命题一、已知(O)为(Delta ABC)内的一点,若(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=vec{0}),则(O)是(Delta ABC)的重心;
证明:必要性,由于(O)是(Delta ABC)的重心,则线段(AD、BE、CF)为三角形的三条中线,
则有(overrightarrow{AB}+overrightarrow{AC}=2overrightarrow{AD}=cfrac{4}{3}overrightarrow{AO}=-cfrac{4}{3}overrightarrow{OA}),
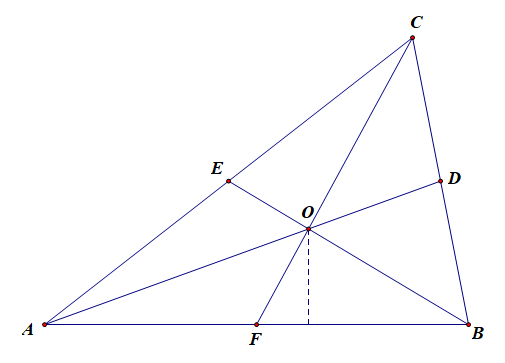
(overrightarrow{BA}+overrightarrow{BC}=2overrightarrow{BE}=cfrac{4}{3}overrightarrow{BO}=-cfrac{4}{3}overrightarrow{OB}),
(overrightarrow{CB}+overrightarrow{CA}=2overrightarrow{CF}=cfrac{4}{3}overrightarrow{CO}=-cfrac{4}{3}overrightarrow{OC}),
故(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC})(=-cfrac{4}{3}(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}))
(=overrightarrow{AB}+overrightarrow{AC}+overrightarrow{BA}+overrightarrow{BC}+overrightarrow{CB}+overrightarrow{CA}=vec{0});
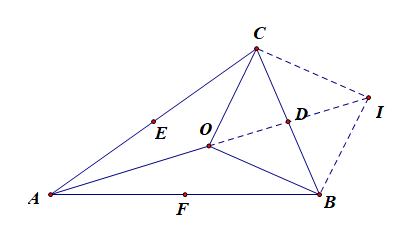
充分性,由(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=vec{0}),得到(overrightarrow{OB}+overrightarrow{OC}=-overrightarrow{OA}),
又(overrightarrow{OB}+overrightarrow{OC}=2overrightarrow{OD}),则(-overrightarrow{OA}=2overrightarrow{OD}),
故点(A、O、D)三点共线,且(AD)为三角形的一条中线;
同理,(BE、CF)为三角形的中线;故(O)是(Delta ABC)的重心;证毕。
在具体题目中的应用形式举例,如【2020宝鸡市二检理科第15题】已知点(P)为三角形( riangle ABC)内部一点,且满足(overrightarrow{PB}+overrightarrow{PC}=overrightarrow{AP}),即(overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PA}=vec{0}),故点(P)是三角形的重心。
- 命题二、(O)是(Delta ABC)的重心,则(S_{Delta AOB}=S_{Delta BOC}=S_{Delta COA});
证明:(O)是(Delta ABC)的重心,令边(AB)上的高线为(h),
则(S_{Delta AOB}=cfrac{1}{2}cdot ABcdot cfrac{h}{3}=cfrac{1}{3}S_{Delta ABC}),
同理,(S_{Delta BOC}=cfrac{1}{3}S_{Delta ABC}),(S_{Delta AOC}=cfrac{1}{3}S_{Delta ABC}),
故(S_{Delta AOB}=S_{Delta BOC}=S_{Delta COA});
- 命题三、已知(D、E、F)是(Delta ABC)的边(BC、AC、AB)的中点,则(overrightarrow{AD}+overrightarrow{BE}+overrightarrow{CF}=vec{0});
证明:已知(D、E、F)是(Delta ABC)的边(BC、AC、AB)的中点,(O)是(Delta ABC)的重心,
则(overrightarrow{AD}=cfrac{1}{2}(overrightarrow{AB}+overrightarrow{AC})),(overrightarrow{BE}=cfrac{1}{2}(overrightarrow{BC}+overrightarrow{BA})),(overrightarrow{CF}=cfrac{1}{2}(overrightarrow{CA}+overrightarrow{CB})),
故(overrightarrow{AD}+overrightarrow{BE}+overrightarrow{CF})(=cfrac{1}{2}(overrightarrow{AB}+overrightarrow{AC}+overrightarrow{BC}+overrightarrow{BA}+overrightarrow{CA}+overrightarrow{CB}) =vec{0});
- 命题四、平行四边形(ABCD)的中心是(O),(P)为平面上任意一点,则(overrightarrow{PO}=cfrac{1}{4}(overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}));
证明:平行四边形(ABCD)的中心是(O),(P)为平面上任意一点,
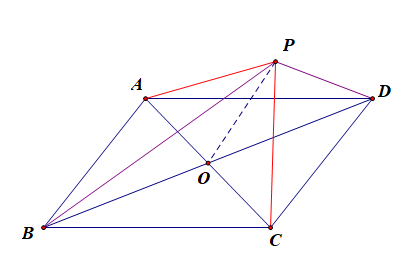
则在(Delta PAC)中,(overrightarrow{PA}+overrightarrow{PC}=2overrightarrow{PO}),在(Delta PBD)中,(overrightarrow{PB}+overrightarrow{PD}=2overrightarrow{PO}),
故(overrightarrow{PA}+overrightarrow{PC}+overrightarrow{PB}+overrightarrow{PD})(=4overrightarrow{PO}),
即(overrightarrow{PO}=cfrac{1}{4}(overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}));
三角形外心
- 外心:三角形的三条边的中垂线交点,也是外接圆的圆心;
- 已知(O)为(Delta ABC)内的一点,满足(|overrightarrow{OA}|=|overrightarrow{OB}|=|overrightarrow{OC}|),则(O)是(Delta ABC)的外心;
三角形垂心
- 垂心:三角形的三条边的高线的交点。
- 命题一、已知(O)为(Delta ABC)内的一点,满足(overrightarrow{OA}cdotoverrightarrow{OB}=overrightarrow{OA}cdotoverrightarrow{OC}=overrightarrow{OB}cdotoverrightarrow{OC}),则(O)是(Delta ABC)的垂心;
证明:由于(overrightarrow{OA}cdotoverrightarrow{OB}=overrightarrow{OA}cdotoverrightarrow{OC}),则(overrightarrow{OA}cdot(overrightarrow{OB}-overrightarrow{OC})=0),
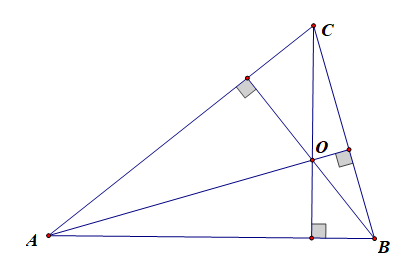
即(overrightarrow{OA}cdotoverrightarrow{CB}=0),则(OAperp BC),
同理可得(OBperp AC),(OCperp AB),故(O)是(Delta ABC)的垂心;
- 命题二、已知(O)为(Delta ABC)所在平面内的一点,且(|overrightarrow{OA}|^2+|overrightarrow{BC}|^2)(=|overrightarrow{OB}|^2+)(|overrightarrow{CA}|^2)(=|overrightarrow{OC}|^2+)(|overrightarrow{AB}|^2),则(O)是(Delta ABC)的垂心;
三角形内心
- 内心:三角形的三个内角平分线的交点,也是内切圆的圆心;
- 命题一、(O)为(Delta ABC)的内心的充要条件是
(overrightarrow{OA}cdot(cfrac{overrightarrow{AB}}{|overrightarrow{AB}|}-cfrac{overrightarrow{AC}}{|overrightarrow{AC}|}))(= overrightarrow{OB}cdot(cfrac{overrightarrow{BA}}{|overrightarrow{BA}|}-cfrac{overrightarrow{BC}}{|overrightarrow{BC}|}))(=overrightarrow{OC}cdot(cfrac{overrightarrow{CA}}{|overrightarrow{CA}|}-cfrac{overrightarrow{CB}}{|overrightarrow{CB}|})=0)
证明:充分性,如图,向量(overrightarrow{AB})、(overrightarrow{AC})的单位向量分别是(overrightarrow{AE})、(overrightarrow{AD}),
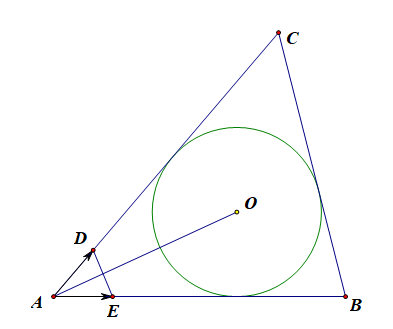
则(Delta ADE)为等腰三角形,
由(overrightarrow{OA}cdot (cfrac{overrightarrow{AB}}{|overrightarrow{AB}|}-cfrac{overrightarrow{AC}}{|overrightarrow{AC}|}))(=overrightarrow{OA}cdot (overrightarrow{AE}-overrightarrow{AD}))(=overrightarrow{OA}cdot overrightarrow{DE}=0),
故(OA)为(angle A)的平分线;同理可得(OB)、(OC)分别为(angle B、angle C)的平分线;
故点(O)是(Delta ABC)的内心。
必要性,由点(O)是(Delta ABC)的内心,则可知(OA)为(angle A)的平分线,
故容易知道(overrightarrow{OA}cdot overrightarrow{DE}=0),
即(overrightarrow{OA}cdot(cfrac{overrightarrow{AB}}{|overrightarrow{AB}|}-cfrac{overrightarrow{AC}}{|overrightarrow{AC}|})=0),
同理可知$ overrightarrow{OB}cdot(cfrac{overrightarrow{BA}}{|overrightarrow{BA}|}-cfrac{overrightarrow{BC}}{|overrightarrow{BC}|})$$=overrightarrow{OC}cdot(cfrac{overrightarrow{CA}}{|overrightarrow{CA}|}-cfrac{overrightarrow{CB}}{|overrightarrow{CB}|})=0$,证毕。
-
命题二、记(overrightarrow{AB}、overrightarrow{BC}、overrightarrow{CA})的单位向量为(vec{e_1})、(vec{e_2})、(vec{e_3}),则(O)为(Delta ABC)的内心的充要条件是(overrightarrow{OA}cdot (vec{e_1}+vec{e_3})=overrightarrow{OB}cdot (vec{e_1}+vec{e_2})=overrightarrow{OC}cdot (vec{e_2}+vec{e_3})=vec{0})。
-
与向量(vec{a})共线的单位向量为两个,(pmcfrac{vec{a}}{|vec{a}|});
解题经验
在具体的题目求解中,关于多个向量的线性表示形式,其难点往往是其系数的恰当拆分。
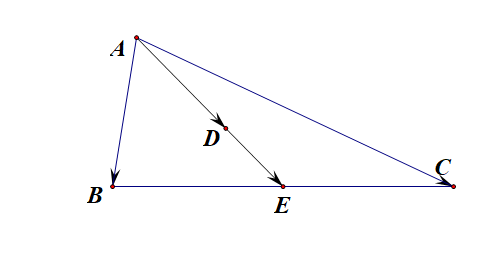
已知(overrightarrow{AB}+overrightarrow{AC}=3overrightarrow{AD}),则(3overrightarrow{AD}=2overrightarrow{AE}),则(overrightarrow{AD}=cfrac{2}{3}overrightarrow{AE}),可知点(D)为( riangle ABC)的重心;