思维训练|一道初中动态问题的初高中解法对照

前言

下述题目是初三的一道数学题目；

如图，在矩形 (ABCD) 中，(AB=3)，(AD=4)，(P)是(AD)上的动点，(PEperp AC)于点(E)，(PFperp BD)于点(F)，则(PE)+(PF)的值为【(quad)】

$A.cfrac{12}{5}$ $B.2$ $C.cfrac{5}{2}$ $D.1$

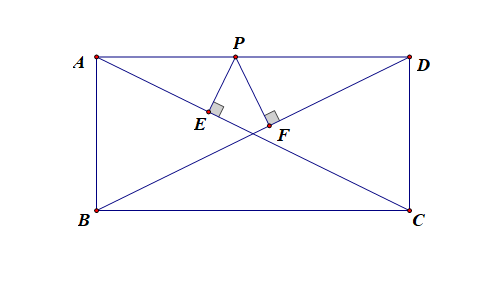
法1：用动态的观点处理问题，初中或高中解法，特殊位置法，此种思路的优越性，类似于将两个变量集中为一个变量；

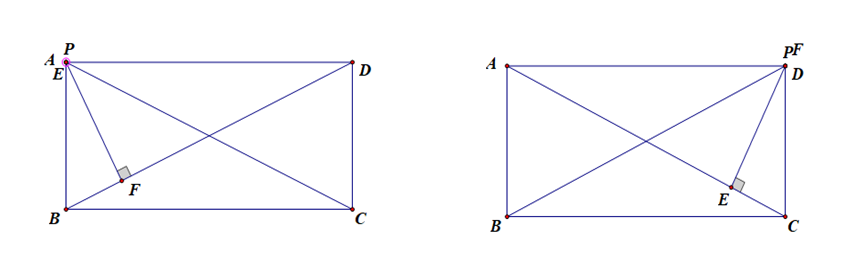
解析：当点(P)在线段(AD)上运动时，线段 (PE) 和 (PF)是变化的，但结合选项可知，和为定值；

故可利用特殊位置，如点 (P) 移动到线段 (AD) 的端点(A)[移动到点 (D)时类比求解]时，来计算所求的线段和；

由于(AB=3)，(AD=4)，则(BD=5)，由等面积法可知，(cfrac{1}{2} imes 3 imes 4=cfrac{1}{2} imes 5 imes PF)，

求得(PF=cfrac{12}{5})，此时(PE=0)，故(PE+PF=cfrac{12}{5})；故选(A)；

法2：用动态的观点处理问题，初中或高中解法，特殊位置法，此种思路的优越性，类似于让两个变量相等；

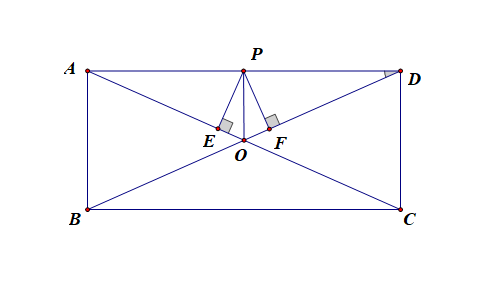
解析：当点 (P) 为线段 (AD)的中点时，容易知道(OPperp AD)，

且(OP=cfrac{3}{2})，(AP=2)，(OA=cfrac{5}{2})，(PE=PF)，

由等面积法可知，(cfrac{1}{2} imes OP imes AP=cfrac{1}{2} imes OA imes PE)，解得(PE=cfrac{6}{5})

故(PE+PF=2PE=cfrac{12}{5})；故选(A)；

法3：用初中平面几何知识求解，运用全等和对称等方法，将折线的长度整合为线段的长度[曲化直]；

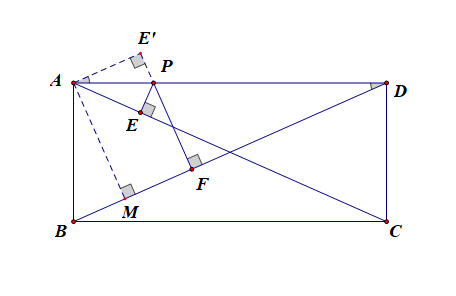
解析：延长 (FP) 到(E')，过点 (A) 做(AE'perp FP)，垂足为(E')，

则由于(AE'//BD)，(angle E'AP=angle ADB=angle DAE)，又(AP)公用，故(Rtangle AE'Pcong Rtangle AEP)，

故(PE=PE')，从而问题转化为求 (E'F)的长度；又(E'F=AM)，而(AM=cfrac{12}{5})，

故(PE+PF=E'F=AM=cfrac{12}{5})；故选(A)；

法4：用高中解析几何求解问题，

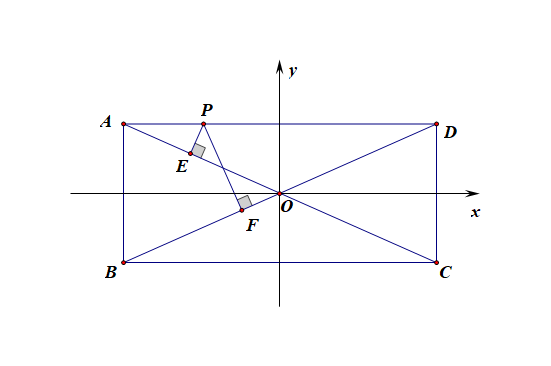
解析：首先建系，建立如图所示的平面直角坐标系，则点(A(-2,1.5))，点(D(2,1.5))，

由于点(P)在线段(AD)上运动，故设(P(x_0,frac{3}{2}))，则(-2leqslant x_0leqslant 2)，

直线(AC: y=-cfrac{3}{4}x)，即(3x+4y=0)，直线(AC: y=cfrac{3}{4}x)，即(3x-4y=0)，

则点 (P(x_0,frac{3}{2})) 到直线(AC)的距离为(PE=cfrac{|3x_0+6|}{sqrt{3^2+4^2}}=cfrac{|3x_0+6|}{5})，

点 (P(x_0,frac{3}{2})) 到直线(BD)的距离为(PF=cfrac{|3x_0-6|}{sqrt{3^2+4^2}}=cfrac{|3x_0-6|}{5})，

又由于 (-6leqslant 3x_0leqslant 6)，故(0leqslant 3x_0+6leqslant 12)，(-12leqslant 3x_0-6leqslant 0)，

故(PE+PF=cfrac{|3x_0+6|}{5}+cfrac{|3x_0-6|}{5}=cfrac{(3x_0+6)-(3x_0-6)}{5}=cfrac{12}{5})；