前言
源头函数
①初中学习过的反比例函数,(y=cfrac{1}{x}),是高中数学中分式函数研究和学习的源头。
结合图像,我们可以自行分析总结其性质:定义域、值域、单调性,奇偶性、周期性、对称性等等;
补充对称性:对称中心为((0,0));对称轴为(y=pm x);
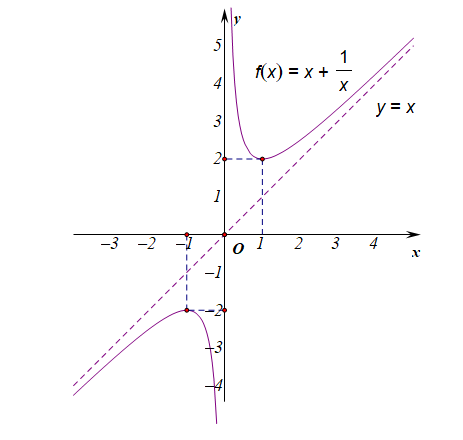
②高中学习过的对勾函数,(y=x+cfrac{1}{x}),是高中数学中分式函数研究和学习的另一个源头。
部分分式
[方法储备]:上述变形中最常用的两个变形为换元法和配凑法;
变换之路
分析:准备作图前的变换,(g(x)=cfrac{x}{x-1}=1+cfrac{1}{x-1});选(y=cfrac{1}{x})为变换作图的模板函数,开始变换如下,
[基本作图]:(y=cfrac{1}{x}) (Rightarrow) (y=cfrac{1}{x-1}) (Rightarrow) (y=1+cfrac{1}{x-1}) (Rightarrow) 对称中心为((1,1));
[快速作图]:相当于基本作图的简化版本,首先找到对称中心((1,1)),过此点分别作直线(x=1)和(y=1),这是两条渐*线;由两条渐*线将*面分为类似的第Ⅰ、Ⅱ、Ⅲ、Ⅳ四个象限,此时观察部分分式的分子[请确保分式的前面是(+)号,如果是(-)号,将减号移到分子上,部分分式的前面仍然写加号],如果分子为正,则在类第Ⅰ和类第Ⅲ象限内作函数的图像,如图所示;
如果分子为负,则在类第Ⅱ和类第Ⅳ象限内作函数的图像;
分析:先做相应的变形,(y=cfrac{5x+1}{2x-1}=cfrac{5(x+frac{1}{5})}{2(x-frac{1}{2})}=cfrac{5}{2}cdot cfrac{x+frac{1}{5}}{x-frac{1}{2}})
(=cfrac{5}{2}cdot (1+cfrac{frac{7}{10}}{x-frac{1}{2}})=cfrac{5}{2}+cfrac{frac{7}{4}}{x-frac{1}{2}})
快速作图:对称中心为((cfrac{1}{2},cfrac{5}{2}));(cfrac{7}{4}>0),在类第Ⅰ和第Ⅲ象限作图,如下所示:
引申结论:①函数(f(x)=b+cfrac{c}{x-a}),(a),(b),(c)为常数,则其对称中心为((a,b));
②如果(c>0),则单调递减区间为((-infty,a))和((a,+infty));如果(c<0),则单调递增区间为((-infty,a))和((a,+infty));
③其解析式必然满足(f(x)+f(2a-x)=2b);
高阶应用
再如(g(x)=cfrac{log_2^x-1}{log_2^x+1}stackrel{log_2^x=m}{Longrightarrow}g(x)=cfrac{m-1}{m+1}),
解后反思:有些复杂的分式,通过换元可以转化为上述比较简单的形式;
- 常用配凑法+分离常数法,或配凑法+分式裂项法,或换元法,
如[配凑法](h(x)=cfrac{x^2-4x+5}{x-2}=cfrac{(x-2)^2+1}{x-2}=(x-2)+cfrac{1}{x-2}),
或[换元法]令(x-2=t),则(x=t+2),
故(h(x)=cfrac{(t+2)^2-4(t+2)+5}{t}=cfrac{t^2+1}{t}=t+cfrac{1}{t})
即(h(x)=t+cfrac{1}{t}=(x-2)+cfrac{1}{x-2})
- 常用取倒数法,或换元法,或配凑同除法
如(n(x)=cfrac{x+1}{x^2+3x+3});则(n(x)=cfrac{x+1}{(x+1)^2+(x+1)+1}=cfrac{1}{(x+1)+cfrac{1}{x+1}+1})
如(g(t)=cfrac{2t}{t^2+9}=cfrac{2}{t+frac{9}{t}});如(h(t)=cfrac{3t+2}{t^2}=cfrac{3}{t}+2(cfrac{1}{t})^2stackrel{frac{1}{t}=m}{Longrightarrow}h(t)=2m^2+3m);
解:当(x=2)时,(y=0),根据题意(xin(m, n])时,(y_{min }=0),则(n=2),
所以(m)的取值范围是(-1leqslant m<2),故选(D).
若定义域为(xin [m,n]),则此时(m)的取值范围是((-1,2]).
延伸关联
分式函数变形后,极有可能和反比例型函数、二次型函数、对勾型函数建立关联,然后向后继续变换即可。