从三点共线到四点共面

前言

请注意其中的类比思维的学习方式。

初中使用，距离表示形式：(|AB|+|BC|=|AC|)
高中使用，斜率表示形式:(k_{AB}=k_{AC})
高中使用向量表示形式：(overrightarrow{OC}=lambdaoverrightarrow{OA}+(1-lambda)overrightarrow{OB}) 或(overrightarrow{AB}=kcdot overrightarrow{AC})

比如线段(AC)和线段(BD)相交或者平行，则可知点(A，B，C，D)四点共面。

要证明(P、A、B、C)四点共面，只要能证明(overrightarrow{PA}=xoverrightarrow{PB}+yoverrightarrow{PC})，

或者对空间任意一点(O)，有(overrightarrow{OA}=overrightarrow{OP}+xoverrightarrow{PB}+yoverrightarrow{PC})

或者(overrightarrow{OP}=xoverrightarrow{OA}+yoverrightarrow{OB}+zoverrightarrow{OC})，其中(x+y+z=1)。

例1如图所示，在空间四边形(ABCD)中，点(E)，(H)分别是边(AB)，(AD)的中点，点(F)，(G)分别是边(BC)，(CD)上的点，且(cfrac{CF}{CB}=cfrac{CG}{CD}=cfrac{2}{3})，则下列说法正确的是【】

①(EF)与(GH)平行；②(EF)与(GH)异面；
③(EF)与(GH)的交点(M)可能在直线(AC)上，也可能不在直线(AC)上；④(EF)与(GH)的交点(M)一定在直线(AC)上；

$A.①④$ $B.④$ $C.①③$ $D.②$

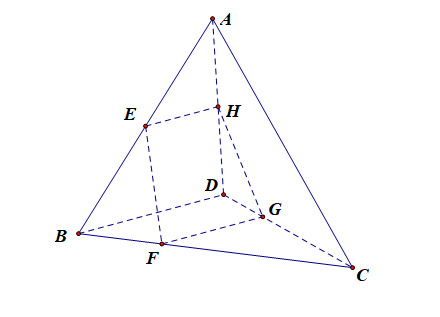
分析：连接(EH)，(FG)，由题意可知，(EH//BD)，(FG//BD)，故(EH//FG)，且有(EF)和(GH)不平行，故四边形(EFGH)为梯形，所以(E,F,G,H)四点共面。故①②错误；

延长(FE)和(GH)必然交予一点，两线的交点一定在平面在(ACD)上，延长(FE)和(CA)必然交予一点，两线的交点一定在平面(ACB)上，

故两线的交点一定在平面(ACD)和平面(ACB)的交线(AC)上，故③错误；故选(B)；

另解：[动态观点]设想线段(FG)平行移动[和(BD)平行]，当(FG)缩减为点(C)时，说明④正确，当(FG)扩充为线段(BD)时，也说明④正确，故①②③错误，故选(B).