一、三角形的心
-
三角形的内心:三角形的三个内角平分线的交点,内切圆的圆心
-
三角形的外心:三角形的三边的中垂线的交点,外接圆的圆心
-
三角形的重心: 三角形的三边的中线的交点。即平衡点。
-
三角形的垂心:三角形的三边的高线的交点。
-
三角形的旁心:三角形的三个外角平分线的交点。【不做研究】
-
注意三角形的上述几个心的向量表示形式。三角形的四心的向量表示
-
当三角形由一般的三角形变化为特殊的三角形时,其几个心的位置关系会发生相应的变化。
-
各种特殊三角形中,如等腰三角形、直角三角形、等腰直角三角形中的情形自行推导。
二、可能涉及的运算与方法
- 勾股定理,比例关系,等面积法,等体积法。
三、正三角形的心
-
正三角形的三线合一:如(angle A)的内角平分线,边(BC)的中线,边(BC)的高线三线合一。
-
正三角形的四心合一:由于上述三线合一,故正三角形的内心、外心、重心、垂心四心合一。
-
正三角形的两圆心合一:正三角形的内切圆圆心、外接圆圆心合二为一。
- 正三角形的内心外心位置:在正三角形的重心位置处,或在正三角形任意一条高线[或中线或垂线]的远离三角形顶点的三等分点处;
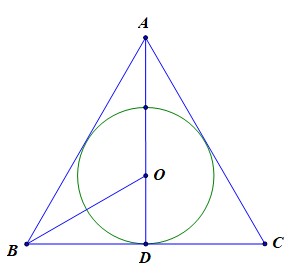
【推导1】思路:如上图所示, (O)为(Delta ABC)的内心,也是重心,
设边长(AB=a),则(BD=cfrac{a}{2}),(AD=cfrac{sqrt{3}a}{2}),
(R{内}=OD=cfrac{1}{3}cdot cfrac{sqrt{3}a}{2}),(R{外}=OA=cfrac{2}{3}cdot cfrac{sqrt{3}a}{2}),
故(R_{内}:R_{外}=1:2);
【推导2】等面积法:(S_{Delta ABC}=S_{Delta OBC}+S_{Delta OAC}+S_{Delta OAB}),
即(cfrac{1}{2} imes BC imes AD=cfrac{1}{2} imes BC imes R_{内}+cfrac{1}{2} imes AC imes R_{内}+cfrac{1}{2} imes AB imes R_{内}),
则(cfrac{1}{2} imes BC imes AD=cfrac{3}{2} imes BC imes R_{内}),
故(R_{内}=cfrac{1}{3}cdot AD=cfrac{1}{3}cdot h),故(R_{外}=cfrac{2}{3}cdot h),
故(R_{内}:R_{外}=1:2);
五、正四面体的心
-
正四面体的内切球球心、外接球球心、棱切球球心,三心合一。
-
正四面体的内切球球心、外接球球心、棱切球球心位置:在正四面体任一高线的四等分点处,且靠近底面。
-
正四面体的棱长为(a),则底面三角形的高为(cfrac{sqrt{3}a}{2}),则正四面体的高为(h=cfrac{sqrt{6}a}{3});
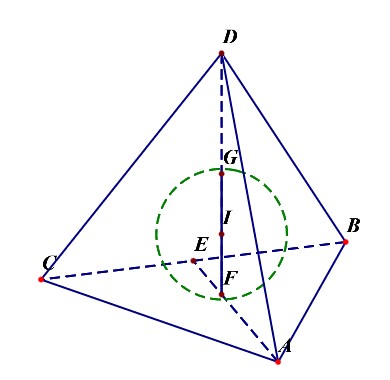
- 正四面体的内切球半径(R_{内}=cfrac{sqrt{6}a}{12}=cfrac{1}{4}h=IF);
推导:等体积法,(V_{D-ABC}=cfrac{1}{3} imes S_{Delta ABC} imes h),(V_{D-ABC}=V_{I-ABC}+V_{I-ABD}+V_{I-BCD}+V_{I-ACD}=cfrac{4}{3} imes S_{Delta ABC} imes R_{内}),
故(R_{内}=cfrac{1}{4}h);
- 正四面体的外接球半径(R_{外}=cfrac{sqrt{6}a}{4}=cfrac{3}{4}h=IC);
推导:由上可知,(R_{外}=cfrac{3}{4}h);
- 正四面体的棱切球半径(R_{棱}=cfrac{sqrt{2}a}{4}=IE);
推导: